基于异方差伪线性模型的纯方位目标要素估计

赵建昕，笪良龙

(海军潜艇学院，山东 青岛266071)

基于异方差伪线性模型的纯方位目标要素估计

赵建昕，笪良龙

(海军潜艇学院，山东 青岛266071)

针对伪线性跟踪估计器假定误差项之间不相关且方差相等，导致利用最小二乘方法得到的目标要素的估计不是最优无偏估计的问题，提出了基于异方差伪线性模型的加权目标运动要素估计方法。该方法考虑了经典的伪线性模型误差项中随时间变化的异方差部分，首先通过方位信息估计出瞬时距离与初始距离比，得到伪线性模型误差项中的异方差部分的估计，然后利用加权最小二乘方法，得到了理论上目标要素的最优无偏估计。数值仿真和实验数据验证表明，该方法优于经典纯方位伪线性化方法。

信息处理技术；目标运动分析；加权最小二乘估计；纯方位

0 引言

纯方位目标要素解算是目标定位和跟踪的重要研究内容，由于方位观测数据的非线性，导致了该问题的复杂性。降低问题的复杂性以及便于工程上实现，将方位的观测模型伪线性化是一类重要的方法，其本质是选择一个新的伪观测量，将非线性观测模型转化为一个伪线性模型，利用最小二乘方法对目标要素进行估计，如文献[1—6]，分别从系统的可观测性、目标要素的最优估计以及观测站的最优机动策略等作了研究，其解决问题的一个基本假定是模型的误差项之间不相关且方差相等，这是对伪线性模型误差项的近似处理，与观测方程作线性化处理时所获得的新的观测误差的非高斯性是不一致的，结果导致了利用最小二乘方法得到的目标要素估计的有偏性和非最优性[7]，目标要素的估计收敛时间长，甚至结果发散，本文针对此问题，提出了基于异方差伪线性模型的纯方位目标要素估计方法。

1 经典伪线性模型及目标要素估计

以下总假定目标作匀速直线运动，只考虑在其运动平面的两维情形。

为研究方便，引入表1记号。

表1 变量符号说明

图1 观测站和目标的运动态势Fig.1 Scenario between observer and target

图2 观测站和目标的相对运动态势Fig.2 Relative scenario between observer and target

由图1、图2知，目标方位与D0,Vmx,Vmy的关系为：

(1)

(2)

记βmk=βm(k)，e(k)=-Dksinν(k)，zk=ywksinβmk-xwkcosβmk，k=0,1,2,…，注意到xm0=D0sinβm0，ym0=D0cosβm0，xmk=xm0+Vmx(tk-t0)，ymk=ym0+Vmy(tk-t0)，则式(2)转化为

zk=sin(βmk-βm0)·D0+(tk-t0)sinβmk·Vmy-
(tk-t0)cosβmk·Vmx+e(k)

(3)

经典的纯方位方法就是以上述模型为基础，并假设e(k)是不相关的同方差的随机误差，利用最小二乘法估计参数D0，Vmy和Vmx，如文献[1-6]，这会导致目标参数估计的有偏性问题[7,9]。显然该模型的误差假设与实际情况是不相符的。

2 异方差伪线性模型及目标要素估计

zk=sin(βmk-βm0)·D0+(tk-t0)sinβmk·Vmy-
(tk-t0)cosβmk·Vmx+Dkν(k)

(4)

式(4)两边同时除D0，整理得

(5)

此时，模型(5)关于参数θ的加权最小二乘估计满足下列方程组：

(6)

综上分析，两个伪线性模型的不同主要表现在：一是异方差伪线性模型考虑了不同时刻的观测误差的不同；二是目标要素的估计方面，异方差伪线性模型中的参数估计利用了加权最小二乘方法，理论上得到了目标要素的最优无偏估计，克服了经典方法目标要素估计的有偏性；三是从数值模拟和实验验证两个方面的结果看，新方法的目标要素估计收敛时间要少于经典方法的目标要素估计收敛时间。

3 目标要素估计及算法实现

3.1 目标相对航向角的估计

当目标和观测站均作匀速直线运动时，利用相对运动规律知，目标可看作为匀速直线运动的物体，假设等时间间隔采样，于是由文献[12]知，假设β1,β2,β3是三个不同的方位角，则目标相对航向角X满足：

(7)

实际计算中，考虑到测量方位的误差，可采用多次计算的平均作为目标相对航向角的估计值。

3.2 瞬时距离与初始距离比的估计

(8)

这里需要注意，式(8)得到的距离比估计是在目标和观测站均作匀速直线运动的条件下成立的，对于该方法得到的估计性能的仿真，详见4.1节。

3.3 算法

假设目标作匀速直线运动，考虑到式(6)的矩阵ATV-1A的可逆性，这里观测站做一次航向机动，速度大小不变，其参数的估计算法为：

1)利用式(7)，估计目标相对航向角；

2)利用式(8)，估计距离比；

3)利用式(6)，估计目标初始距离、速度和航向；

4)观测站机动，此时目标距离记为Dk0，重新利用步骤1)和2)，得到瞬时距离与Dk0的比；

5)利用步骤2)和4)得到的距离比相乘，得到第二阶段瞬时距离与初始距离的比；

6)重复步骤3)。

4 数值仿真与实验验证

下面通过数值模拟和实验数据验证，检验本文方法的有效性和可行性。

4.1 数值仿真

首先假设观测站不做航向和速度机动，考察式(8)的瞬时距离与初始距离比估计量的性能。考虑两类态势：一类是目标接近；二类是目标远离。

以时间总长600 s为例，抽样时间2 s，利用仿真的前50 s方位数据，对目标相对航向角进行估计，进而利用此估计值对距离比进行估计和预测，目标和观测器其他的参数设定见表2。

图3对应的实验序号1，给出了目标接近态势，观测站速度分别为3×1 852/3 600 m/s和6×1 852/3 600 m/s，不同的方位误差的模拟结果。

图4对应的实验序号2，给出了目标远离态势，观测站速度分别为3×1 852/3 600 m/s和6×1 852/3 600 m/s时，不同的方位误差的模拟结果。

从表2的仿真结果看，利用前50 s的方位数据可以比较准确地估计距离比参数，误差均控制在2%以内，方位误差越小，估计误差越小。

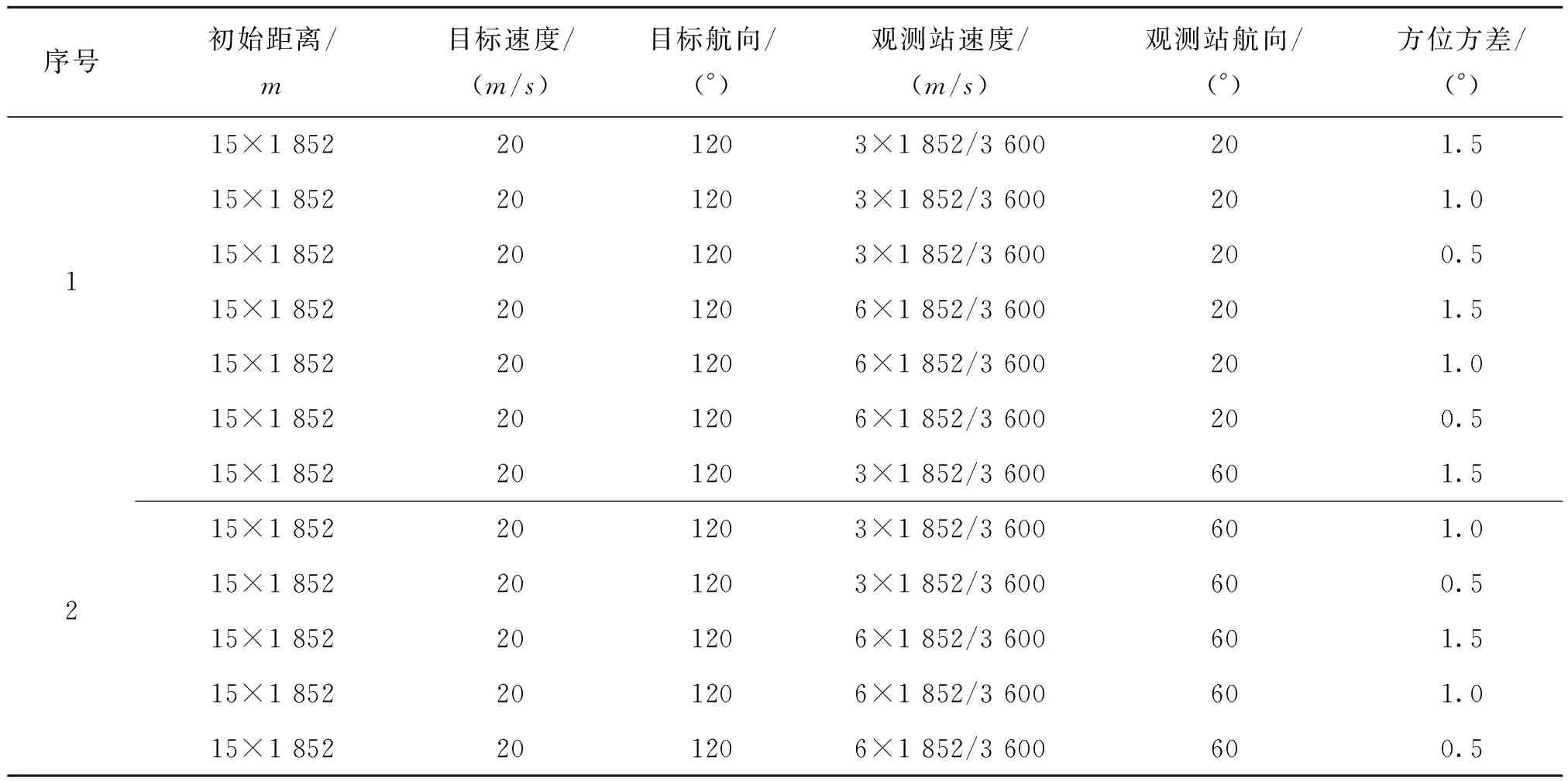
表2 观测站和目标数值模拟要素值

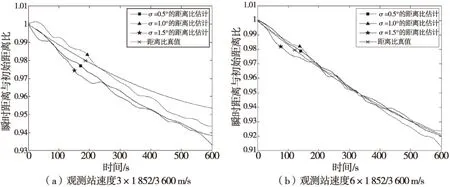
图3 目标接近态势Fig.3 Approaching scenario of target

图4 目标远离态势Fig.4 Removing scenario of target

其次，考察观测站做航向机动，在两类态势下，利用加权算法对目标距离、速度和航向的估计。图5给出了目标初始距离15×1 852m，目标速度20×1 852/3 600m/s，目标航向120°，观测站速度6×1 852/3 600m/s，航向由30°转至50°的远离态势目标要素估计结果。图6给出了目标初始距离15×1 852m，目标速度20×1 852/3 600m/s，目标航向120°，观测站速度6×1 852/3 600m/s，航向由0°转至20°的接近态势目标要素估计结果。从图5和图6的结果看，如果以参数真值的10%误差上下限为收敛域，新方法要优于经典纯方位方法，当方位误差为0.1°时，利用新方法求得的三个参数估计基本上都能在600s左右收敛到10%误差上下限内。

4.2 海试数据验证

为了验证文中的新方法在实际环境中的性能，以下是基于某次海上的实验数据，利用文中给出的方法与经典的伪线性估计算法进行了实证比较。实验方案具体为：

初始时刻，目标航向为104.76°，目标速度为17.56×1 852/3 600m/s，初始方位为264.10°。观测站初始时刻的航向为340.10°，速度为6.72×1 852/3 600m/s。目标和观测站的初始距离为72.86×185.2m，采样时间为2s，观测站从240s开始机动，至360s结束，总用时1 150s。目标和观测站在整个实验过程中的要素值见图7，图8为目标要素的估计结果。从目标要素的估计在真值的上下10%的误差限内来看，加权纯方位算法要优于经典纯方位算法，特别地，在上下10%误差限内，加权纯方位算法估计的目标速度，其波动要小一些。

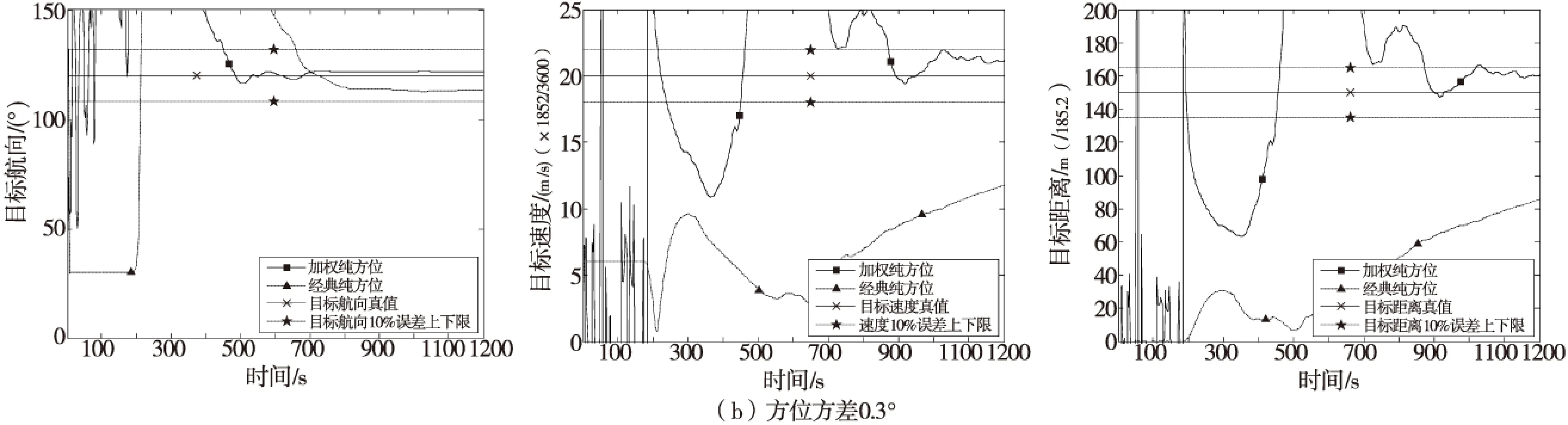
图5 目标远离态势Fig.5 Removing scenario of target

图6 目标接近态势Fig.6 Approaching scenario of target

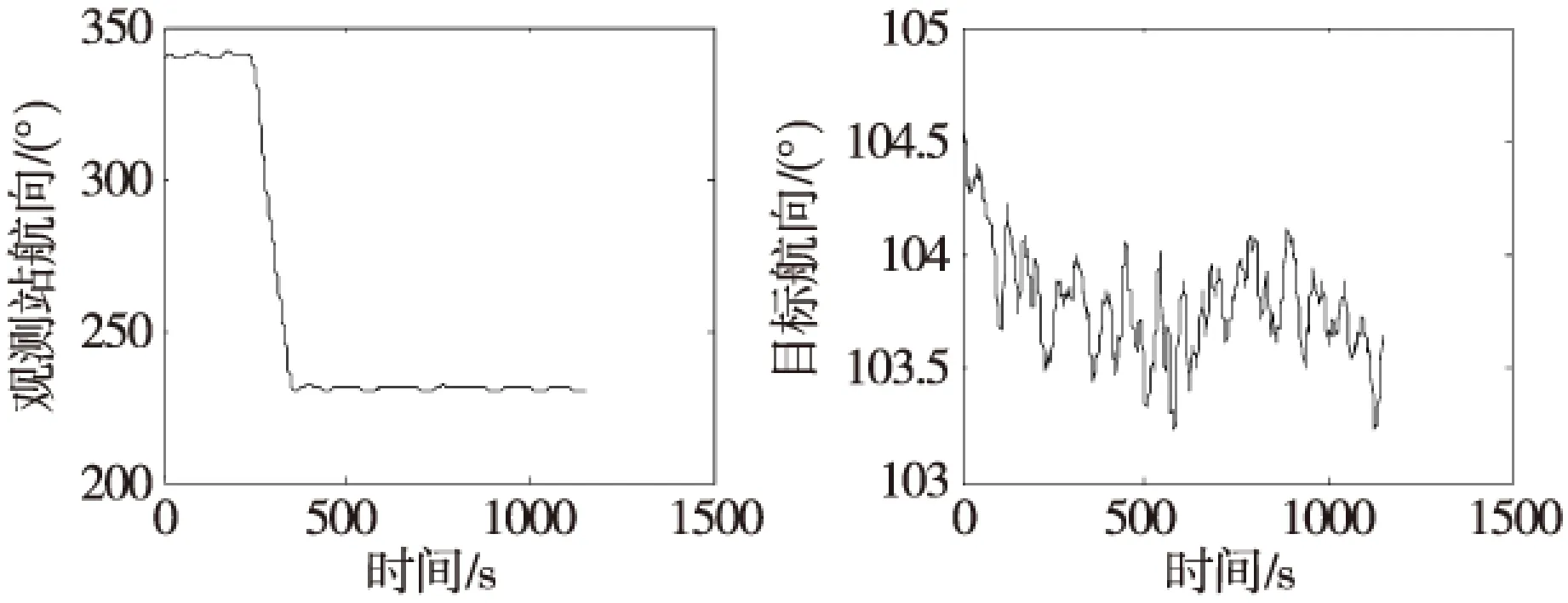
图8 目标要素估计Fig.8 Estimates of target elements

5 结论

本文提出了基于异方差伪线性模型的加权目标要素估计方法。该方法考虑了经典的伪线性模型误差项中随时间变化的异方差部分，首先通过方位信息估计出瞬时距离与初始距离比，得到伪线性模型误差项中的异方差部分的估计，然后利用加权最小二乘方法，得到了理论上目标要素的最优无偏估计。数值模拟和实验数据验证结果表明，该算法与经典的纯方位算法相比，给出的目标要素估计的收敛时间要少，方法是有效可行的。随着方位误差的增加，目标要素的估计也表现出波动性较大，这是下一步需要深入研究的内容。

[1]孙洪胜．基于方位角测量的无源定位算法研究[D].哈尔滨：哈尔滨工程大学，2010．

[2] 赵骁飞.单站纯方位无源探测定位的若干技术的研究[D].上海：上海交通大学，2007.

[3] 许志刚，董志荣．纯方位系统单目标定位与跟踪的拟线性估计器[J].弹道学报，2002，14(3)：10-16．

[4] 杨国胜，窦丽华，侯朝桢．基于纯角度的三维运动目标可观测性研究[J].兵工学报，2004，25(2)：182-185.

[5] 刘忠，邓聚龙．多传感器系统纯方位定位与可观测性分析[J].火力与指挥控制，2004，29(5)：79-87．

[6] 赵建昕，笪良龙，徐国军，等．线性等式约束下的纯方位目标运动分析[J].应用声学，2014，33(2)：120-129．

[7] 夏佩伦.目标跟踪与信息融合[M].北京：国防工业出版社，2010.

[8]AidalaVJ.Kalmanfilterbehaviorinbearings-onlytrackingapplication[J].IEEETransactionsonAerospaceandElectronicSystems, 1979, 15(1): 29-39.

[9]AidalaVJ,NordoneSC.Biasedestimationpropertiesofthepseudolineartrackingfilter[J].IEEETransactionsonAerospaceandElectronicSystems, 1982, 18(4)：432-441.

[10]Aidala.VJ.Behaviorofthekalmanfilterappliedtobearings-onlytargetmotionanalysis[R].Navalunderwatersystemscenter,NUSCtech，USA：1976.

[11] 徐利治．现代数学手册—随机数学卷[M].武汉：华中科技大学出版社，2000:252-253．

[12] 刘进忙，姬红兵，左涛．纯方位观测的航迹不变量目标跟踪算法[J].西安电子科技大学学报，2008，35(1)：49-53．

Target Bearings-only Elements Estimation Based on Heteroscedastic Pseudo-linear Model

ZHAO Jianxin, DA Lianglong

(Navy Submarine Academy, Qingdao 266071, China)

The estimation of target elements using least square method are not optimal unbiased estimates as the pseudo linear target tracking filter based on non-correlation errors of model and equal variance.In order to solve the question, a heteroscedastic pseudo-linear model was established by using new parameter variables, based on the model, a weighted method for target motion analysis was presented. The heteroscedastic part of error of the pseudo-linear model was considered. Firstly, the ratio of instantaneous distance and initial distance were estimated by using bearings and the estimate of the heteroscedastic part of model error was obtained, then, By using the weighted least squared method, the optimal unbiased estimates of target elements were obtained in theory. Numerical simulation results showed that the new method was better than the classical pseudo-linear methodt.

information processing technology；target motion analysis；weighted least square estimate；bearings-only

2016-12-20

总装预研究项目资助(51303080302-5)

赵建昕(1969— )，男，山东青岛人，博士，副教授，研究方向：水声信号处理。E-mail:qy_zjx@eyou.com。

O428

A

1008-1194(2017)02-0007-06