基于模态分析和经验模态分解的弹体加速度处理

孙 猛，徐 鹏，2，沈大伟，王丽利

(1.中北大学电子测试技术国家重点实验室，山西 太原 030051；2.中北大学理学院，山西 太原 030051； 3.西北工业集团有限公司，陕西 西安 719043)

基于模态分析和经验模态分解的弹体加速度处理

孙 猛1，徐 鹏1，2，沈大伟1，王丽利3

(1.中北大学电子测试技术国家重点实验室，山西 太原 030051；2.中北大学理学院，山西 太原 030051； 3.西北工业集团有限公司，陕西 西安 719043)

针对气体炮发射过程中弹体加速度信号目前尚无有效的、准确的处理方法，提出了基于模态分析与经验模态分解算法(EMD)的气体炮发射过程弹体加速度信号处理方法。该方法结合模态分析与EMD获得气体炮发射过程弹体结构响应与谐振，再将弹体结构响应从实测加速度信号中剔除，从而较为精确地获得弹体的刚体加速度变化情况。通过对加速度进行二次积分得到的位移与实际行程之间的相对误差较小，试验表明，通过该方法处理的弹体加速度信号准确有效。

气体炮；弹体结构响应；模态分析；经验模态分解

0 引言

能够模拟真实弹丸的发射环境对于炮弹、引信的研发、改进、测评是十分重要的。在现有的模拟装置中，气体炮能够较好地实现对弹体发射环境的模拟，因此被广泛应用[1]。虽然气体炮种类众多，原理多样，但弹丸能否达到特定的运动参数，还需进行一定的动态存储测试[2]。

而对于存储测试所获得的加速度数据都要进行数据处理，国内外一般的处理方法包括零点漂移的修正和滤波处理，通常依靠模态分析和频谱分析选取截止频率进行滤波[3]。但对于类似本文这种新型气体炮的非平稳加速度信号，一部分有用的高频信号可能会隐藏于噪声中而被滤去，最终导致处理后的加速度准确性较差。本文针对上述问题，提出了基于模态分析和经验模态分解法(EMD)的气体炮发射过程弹体加速度信号处理方法。

1 模态分析与EMD基本理论

1.1 模态分析

由机械振动理论可得，N自由度系统的振动微分方程为：

(1)

对于本系统，弹体既不受约束，也不受任何外界激励。因此，F(t)=0。

式(1)的特征值与特征向量即为系统各阶固有频率与相应主振型的解[4]。

1.2 EMD算法

EMD是由N E.Huang 提出的，它是完全基于信号本身，将信号分解成不同时间尺度特征的本征固有模态函数(IMF)分量和一个残量。与傅里叶变换、小波变换最本质区别在于无需设定基函数，因此非常适合于这种非平稳的信号分析[5]。

EMD 基于以下三个假设：1)信号至少有两个极值点，即一个极大值点和一个极小值点；2)极值点的时间推移间隔决定信号的特征时间尺度；3)如果信号存在曲折点而缺乏极值点，通过一次或多次微分找到极值点，再进行分解信号[6-7]。

EMD具体步骤：

1)由信号s(t)极大值、极小值包络线的局部均值组成序列m1(t)，求得：

h1(t)=s(t)-m1(t)

(2)

若h1(t)满足IMF条件，则h1(t)为第一个IMF分量。

2)若h1(t)不满足IMF条件，则将h1(t)作为原始数据，重复步骤1)k次：

h1k(t)=h1(k-1)(t)-m1k(t)

(3)

使得h1k(t)满足IMF条件，记第一个IMF分量：c1(t)=h1k(t)。

3)现从s(t)中减去c1(t)，可得到残差：

r1(t)=s(t)-c1(t)

(4)

将r1(t)作为原始信号，重复步骤1)和2)，得到信号的第二个分量。以此类推，一直到rn(t)变成单调函数循环结束，得到n个IMF分量。这样便把信号分解成n个IMF分量和一个残量rn(t)之和，即：

(5)

各个IMF分量分别包含了该信号从高频到低频的成分，并且随着信号的变化而变化[8]。

2 弹载测试仪实测加速度信号处理

运用弹载存储测试仪对气体炮发射过程的弹体加速度进行测试，所测到的弹体轴向加速度曲线如图1所示。

图1 实测弹体加速度曲线Fig.1 Measured acceleration of projectile

弹载测试仪所得到的弹体加速度信号主要由以下几部分构成：一是弹体在火药燃气推动和预存储空气阻力共同作用下弹体刚体加速度信号；二是测试点相对于弹体质心的各阶轴向振动加速度信号；三是由于加速度传感器安装结构和传感器对主激励的余响应产生的谐振，通常频率较高。对弹体轴向加速度曲线(即图1)进行EMD分解，得到12个IMF分量和1个残量r13，其中分量c1～c4以及各自的功率谱(PSD)如图2、图3所示。

从图3(a)中的IMF1功率谱可以看出，在43 kHz附近出现谐振峰，由图3(e)可以看出，分量c1～c4的功率谱之和的主波峰位于2.21 kHz，3.61 kHz，5.59 kHz，7.62 kHz处。

图2 EMD 分解的c1～c4Fig.2 c1～c4of EMD

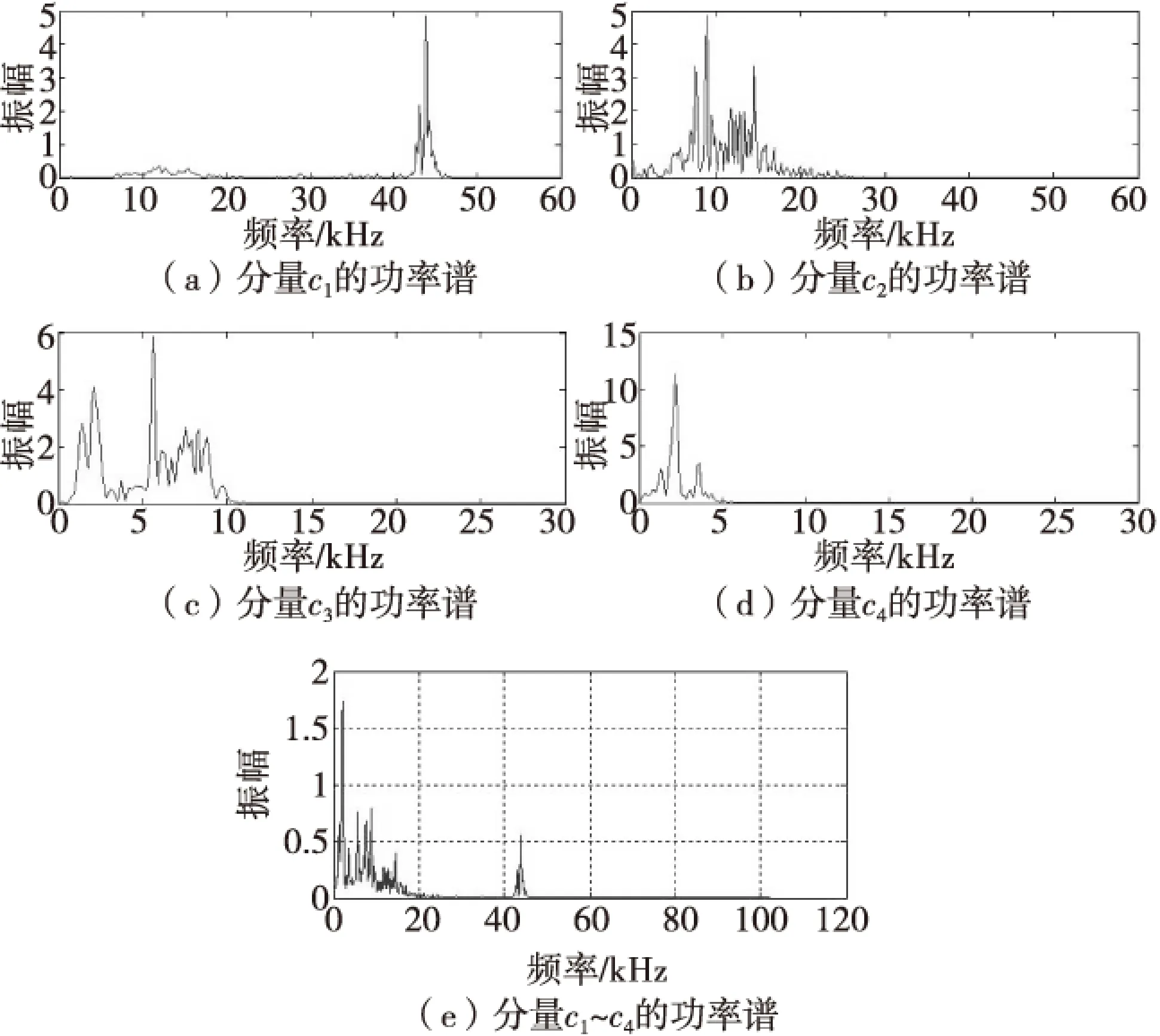
图3 c1～c4的功率谱Fig. 3 PSD of c1～c4

3 仿真验证分析

3.1 弹体模态分析

首先建立含有测试仪的试验弹体ANSYS有限元模型，如图4所示。

图4 弹体有限元模型Fig.4 Finite element model of projectile

该试验弹主要由壳体、测试仪、配重块组成，弹体长868 mm，最大直径180 mm。弹体各部分的材料属性参数如表1所示。

表1 各部件的材料参数

由于测试仪与弹体之间采用螺纹刚性连接方式，弹载测试仪本身的结构响应对加速度的影响得到显著减少，因此本文忽略测试仪自身影响。

运用ANSYS对含有测试仪的试验弹体有限元模型进行模态分析，得出在自由状态下的前30阶的固有频率以及各阶主振型，如表2所示。装有测试仪的弹体前6阶固有频率均接近0，即为刚体模态。从第7阶开始为非刚体模态，其振型主要是弹轴方向的弯曲、扭转、拉伸压缩；其中弯曲振型通常成对出现，相应的弯曲面垂直，固有频率几乎相等。本文主要研究轴向加速度信号，因此只列出轴向拉伸压缩振型的固有频率，其振型图如图5所示。

表2 试验弹体各阶固有频率

图5 弹体的轴向拉伸压缩振型图Fig.5 The tensile and compression modes figures of projectile

通过对比表2的固有频率与图3(e)的波峰位置，可以发现分量c1～c4的主要能量集中位置2.21 kHz，3.61 kHz，5.59 kHz，7.62 kHz分别与弹体轴向拉伸压缩固有频率2 414.5 Hz，3 645.7 Hz，5 642.3 Hz，7 677.5 Hz一一对应。

由此验证，分量IMF1～IMF4的能量集中频率都与弹体各阶轴向拉伸压缩的固有频率相对应。因此认为分量IMF1～IMF4之和即为弹体的结构响应；并且，通过分量IMF1～IMF4的功率谱数值表明，弹体结构响应主要是低阶轴向拉伸压缩振型，高阶振型相对较少。

3.2 重构弹丸的刚体加速度

从实测加速度信号中将弹体结构响应信号以及谐振信号去除，即可获得弹丸的刚体加速度a(t)：

重构的弹丸的刚体加速度如图6所示，其峰值可达到12 623g。

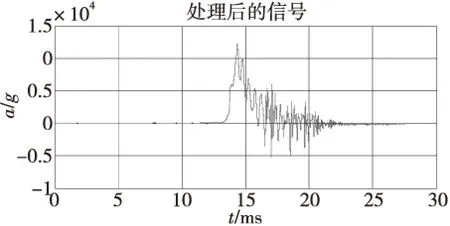
图6 重构的弹体加速度曲线Fig.6 Reconstructed acceleration of projectile

最后，由该加速度进行二次积分得到位移3.58 m，与试验实际行程3.27 m比较相近，相对误差为8.66%。

4 结论

本文提出了基于模态分析与EMD的气体炮发射过程弹体加速度信号处理方法。该方法运用模态分析获得弹体轴向结构的固有频率；同时对实测的加速度信号运用EMD求解获得弹体结构响应与谐振，再将弹体结构响应与谐振从实测加速度中去除，从而较为精确地获得弹体的刚体加速度。该方法处理后的加速度进行二次积分所得到的位移变化与实际行程的相对误差较小，试验表明：该方法处理后的弹体加速度信号准确有效，能够运用于气体炮发射过程弹体加速度信号处理。

[1]齐杏林,杨清熙,文健,等.基于气体炮的引信动态模拟方法综述[J].探测与控制学报,2011,33(4):1-5.

[2] 徐鹏,祖静,范锦彪.高g值加速度冲击试验技术研究[J].振动与冲击, 2011,30(4):241-244.

[3] 范锦彪,祖静,徐鹏,等.弹丸侵彻混凝土目标减加速度信号的处理原则[J].探测与控制学报,2012,34(4):1-5.

[4] 尚雅玲,惠江海,许皓文.超音速反舰导弹引战系统频响特性[J].探测与控制学报,2015,31(3):1-4.

[5] 郝慧艳,李晓峰,孙运强,等.侵彻过程弹体结构响应频率特性的分析方法[J].振动测试与诊断, 2013(02):307-310.

[6] 邵忍平,曹精明,李永龙.基于EMD小波阈值去噪和时频分析的齿轮故障模式识别与诊断[J].振动与冲击, 2012(8):96-101.

[7]Huang N E.Shen Z, Long S R, et al.The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis [J].Proceedings of the Royal Society of London.Series A: Mathematical, Physical and Engineering Sciences, 1998, 454 (1971):903-995.

[8] 王燕，薛云朝，马铁华.基于EMD和最小二乘法的零漂处理方法研究[J].北京理工大学学报，2015(2)：118-122.

The Projectile Acceleration Processing Method Using Modal Analysis and Empirical Mode Decomposition

SUN Meng1, XU Peng1,2, SHEN Dawei1, WANG Lili3

(1.State Key Laboratory of Electronic Measurement Technology, North University of China, Taiyuan 030051, China；2.School of College of Science, North University of China, Taiyuan 030051, China；3. Northwest Industrial Group Co., Ltd., Xi’an 719043, China)

Aiming the fact that there is no effective and accurate processing method for processing air gun and missile acceleration signal, a method based on modal analysis and empirical mode decomposition (EMD) was proposed. The method combined with modal analysis and the empirical mode decomposition (EMD) algorithm to obtain the projectile structural response and resonance during the gas gun launching process the, the structural response of missile body removed from the measured acceleration signal, so as to more accurately get the change of the acceleration of projectile rigid body. By quadratic integral of acceleration, the displacement and the relative error of the actual schedule was less. Testing results showed that the method was accurate and effective.

gas gun; projectile structural response; modal analysis; empirical mode decomposition

2016-10-17

孙猛(1990—)，男，内蒙古赤峰人，硕士研究生，研究方向：动态测试与智能仪器。E-mail:1228114308@qq.com。

TJ410

A

1008-1194(2017)02-0120-04