基于粒子群优化支持向量机神经网络的弹丸落点预报

马 焱，赵捍东，黄 鑫

(中北大学机电工程学院，山西 太原030051)

基于粒子群优化支持向量机神经网络的弹丸落点预报

马 焱，赵捍东，黄 鑫

(中北大学机电工程学院，山西 太原030051)

针对目前弹丸落点预报方法预报时间较长和精度不高的问题，提出了基于粒子群(PSO)优化的支持向量机(SVM)神经网络预测方法。该方法采用PSO优化算法优化SVM训练参数，以获得最优SVM神经网络落点预测模型。在此基础上，使用卡尔曼滤波处理外弹道数据形成神经网络训练数据，进行落点预报仿真测试。仿真结果表明，射程最大误差为7.371 m，横偏最大误差为0.886 m；落点预报时间在35 ms之内，比数值积分法快了一个数量级，为弹丸落点预报的实际应用提供了一种途径。

神经网络；PSO算法；SVM；落点预测

0 引言

现代战争中，实现精确打击已是弹药发展的重中之重，其中弹丸落点的准确预测是实现精确打击的重要前提[1]。落点预测制导律要求在无控状态下预报弹丸的实际落点，计算其与目标点的弹道偏差，据此下达控制指令以调节落点偏差，实现弹道修正，从而减小脱靶量[2]。采用落点预测制导律时，落点预报的精度直接关系到制导精度，因此快速并精确地落点预报对实现弹道修正，提高制导精度有十分重要的意义。

用数值解法进行弹丸落点的预测是经典的做法，然而数值解法是建立在现有外弹道方程基础上的，落点预报精度过多依赖于弹载计算机的处理能力，且数值计算量大、解算时间长和迭代过程中易产生大的累积误差，同时外弹道模型与实际飞行轨迹之间的偏差也会给落点预测带来误差。近些年来，人们提出了各种落点预报方法, 史金光等人[3]将卡尔曼滤波引入落点预报中，能降低随机噪声和累积误差对预报精度的影响，但预报时间较长；曹营军等人[4]利用改进型BP神经网络算法预报落点，能有效避免累积误差的产生，但是在解算时间和精度方面略有不足。本文针对此问题，利用SVM神经网络良好的泛化能力和容错能力，提出了基于PSO优化SVM神经网络的弹丸落点预报方法。

1 SVM神经网络及PSO优化算法原理

1.1SVM理论

SVM是通过学习已知数据来总结数据之间的规律,学习过程并不需要任何有关数据的经验,因此在处理非线性问题时具有很强的优势[5]。

SVM适于解决小样本、非线性回归估计问题[6]。SVM的回归模型描述如下[7-8]：

假设训练样本集为D={(xi,yi)/i=1,2，…，n},xi∈Rn,yi∈R。式中，n为样本数，xi为输入变量，yi为输出变量。SVM回归的基本思想是利用非线性函数将输入空间数据映射到高维特征空间，并在该空间用函数f(x)=〈w,x〉+b(w为权值向量，其维数反应了特征空间的维数；b为偏置)进行线性回归。

参数w和b通过最小化正则风险函数获得 ：

引入松弛变量式：

(1)

(2)

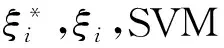
(3)

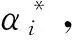
(4)

则回归方程的表达式可描述为：

(5)

式(5)中，K(xi,x)是核函数。核函数的引入使得高维空间中的内积运算可以通过输入空间中的函数来实现，避免了维数灾害[9]，常用的核函数有径向基核函数，多项式核函数等等。由于径向基核函数只有一个变量需确定，径向基核函数构造的SVM训练参数相对较少，较易确定，因而本文采用的是高斯径向基函数，如式:

(6)

式(6)中，σ是核函数的参数。

惩罚因子C、不敏感损失函数ε以及核函数的参数σ决定了SVM回归模型的性能：惩罚参数C决定对较大拟合偏差所采取的惩罚力度，C取值过大，可能会导致过学习，而取值过小可能导致欠学习。核函数的参数σ反映了训练数据集的特性，决定了解的复杂性，影响学习机的泛化能力。损失函数ε表示对估计函数在误差上的期望值，它的取值一定程度上决定了构造回归函数的支持向量的个数。如何更好地选择合适的参数是研究SVM的关键，本文提出利用PSO算法优化SVM的相关参数。

1.2SVM神经网络结构

通过核隐式映射，将输入空间X与输出空间Y联系起来了。非线性函数可以通过核特征空间中的线性学习器得到，其中相应的SVM的训练网络如图1所示。

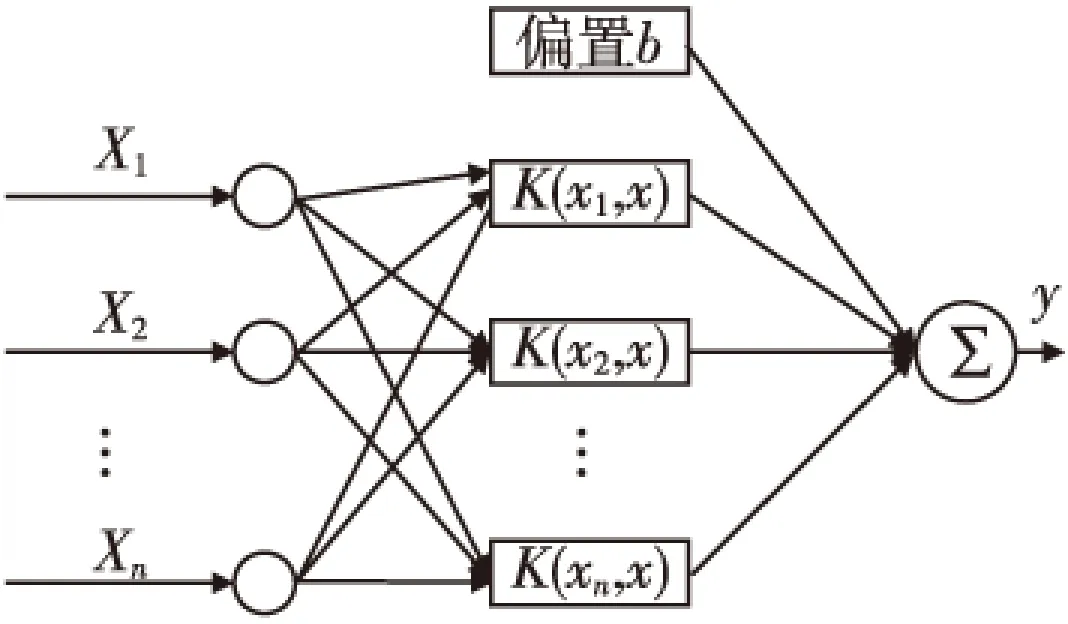
图1 SVM神经网络拓扑结构Fig.1 Topology of support vector machine neural network

1.3PSO优化算法

PSO优化算法是一种基于群体的智能寻优算法，源于对鸟群捕食行为的研究。PSO初始化为一群随机粒子，每个粒子代表解空间的一个候选解，解的优劣程度由适应度函数决定，其中适应度函数根据优化目标定义。粒子们追随当前的最优粒子在解空间中搜索，通过迭代找到最优解。在每一次迭代中，粒子通过跟踪个体最优解pbest和全局最优解gbest来更新粒子的速度和位置，个体最优解是指粒子本身到当前时刻为止找到的最好解；全局最优解是指整个种群到当前时刻找到的最好解[7-9]。假设在一个Q维空间中搜索由n个粒子组成的群体，设第i个粒子的位置为D=(di1,di2,…，diQ)，速度为V=(vi1,vi2，…，viQ)。第i个粒子的位置和速度根据下列方程变化：

(7)

式中，t为进化代数；rand为0到1之间的随机数；ω为惯性权值，用于平衡全局搜索和局部搜索；β为约束因子，用于控制速度的权重；c1,c2是学习因子。

1.4 基于PSO优化算法的SVM优化过程

惩罚参数C、RBF核参数σ、不敏感损失参数ε的取值对SVM预测性能有着较大影响，为了获取较高预测性能的SVM，则需得到较优的C、σ、ε参数组合。PSO优化算法对这些参数进行优化，优化过程描述为：

1)粒子初始化。由参数C、σ、ε组成一个粒子，并随机产生一组粒子的初始位置和速度。确定粒子个数、惯性权重、加速系数、迭代次数。

3)对每个粒子，将其适应度值与其经历过的最好位置pbest作比较，如果较好，则将其作为当前的最好位置pbest。

4)对每个粒子，将其适应度值与全局所经历的最好位置gbest作比较，如果较好，则将gbest设置为最好粒子的当前位置。

5)根据式(7)更新粒子的速度和位置。

6)检验是否符合结束条件(迭代次数达到了给定的最大次数或达到最小误差要求)，如果符合，则停止迭代；否则转至2)。

2 SVM神经网络的弹丸落点预报

2.1 落点预报非线性方程

结合6D自由度刚体外弹道方程[10]，建立弹丸落点与当前弹丸状态参数的非线性方程，形式为：

A=f(B)

(8)

式(8)中，A为弹丸落点信息，即射程X和横偏Z，B是当前弹丸状态参数。为充分利用实测弹丸状态参数，分别建立射程和横偏关于弹丸状态诸元的函数，形式为：

X=f1(x,y,z,vx,vy,vz,θ)

(9)

Z=f2(x,y,z,vx,vy,vz,β)

(10)

式(9)和式(10)中自变量均表示弹丸飞行状态参数。x,y,z,vx,vy,vz是地面坐标系下的弹丸当前位置分量和速度分量，θ和β为俯仰角和偏航角，X和Z分别为射程和横偏。

2.2 基于PSO优化SVM神经网络的落点预报

由于SVM神经网络具有极强的非线性映射能力,因而可用于弹丸落点预报。其落点预报实质是利用非线性函数将输入空间弹丸飞行状态参数映射到高维特征空间，并在该空间用SVM线性回归方程进行线性组合，来逼近落点预报的非线性方程。采用滤波后的实测弹道参数训练落点预报模型[11-12]，调节网络参数，得到最佳的加权线性组合g(·)，可无限逼近f(·)，即

g(·)=f(·)

完成任意当前弹丸飞行参数对弹丸落点信息的映射,最终得到落点预报的非线性函数,其形式为:

X=g1(x,y,z,vx,vy,vz,θ)

Z=g2(x,y,z,vx,vy,vz,β)

其中，射程和横偏预报函数是相互独立的两个函数。

3 仿真与分析

3.1 落点预报仿真

训练样本必须具有很强的代表性，本文以某加农炮为例，使用经典四阶龙格库塔法，以步长0.01 s解算6D自由度刚体外弹道方程，然后用卡尔曼滤波法处理弹道数据，滤波后的弹道数据作为备选弹丸飞行状态数据。从射角6°到60°的范围内，每隔2°提取一条弹道数据，并在弹丸发射5 s后每3 s采集一次飞行弹道参数，直至飞行结束前5 s结束采样。按与式(9)和式(10)中自变量与因变量一一对应的形式，将弹道数据整合成神经网络的训练数据，共有训练样本有837组。首先从原始训练样本里把训练集和测试集提取出来，然后进行一定的预处理，之后用训练集对SVM进行训练，得到基于PSO优化SVM的落点预报模型，再用该模型来预测测试集，得到模型的预测精度。

在实际应用时，这些输入量数据可以通过弹载的GPS/惯性测量单元，或GPS/惯性测量单元/地磁测量单元获得比较精确的值，数据获取也较为容易。

3.1.1 数据归一化

为保证训练效果和预测精度，需对训练数据进行归一化处理。对于数列b(i)，b(i+1)，b(i+2),…，则归一化处理的数列为x(i)，x(i+1)，x(i+2)…，其中

3.1.2 训练样本构建

如表1所示，对于一组连续的数列x(i),将x(i),x(i+1),x(i+2)，…，x(k+i-1)作为输入矢量，x(k+i)作为输出值，从而建立训练样本。因而，SVM回归模型的训练样本可描述为：

x(k+i)=f(x(i),x(i+1)，…，x(k+i-1)

式中，k为输入矢量的维数。

表1 训练样本构建

3.2 落点预报仿真结果分析

3.2.1 落点预报仿真结果

将未录入训练样本的数据作为测试样本，即训练样本数675组，测试样本数162组。经测试后，得到图2和图3分别表示射程和横偏的预测误差量。

记录每条弹道上预报落点信息，将其与经滤波后的实际落点比较，得到最大误差。统计出射程和横偏上的偏差值，经SVM神经网络输出的预报数据，射程最大预报误差为7.371 8 m，横偏最大预报误差为0.886 1 m，误差控制在了较小的范围内。

为了说明本文方法优于传统方法预报效果，取42°，45°，48°射角的弹道数据作研究对象，分别用数值积分法、改进型BP神经网络法和本文提出的基于PSO优化SVM神经网络预报弹丸落点。分别统计其落点解算信息，如表2所示。

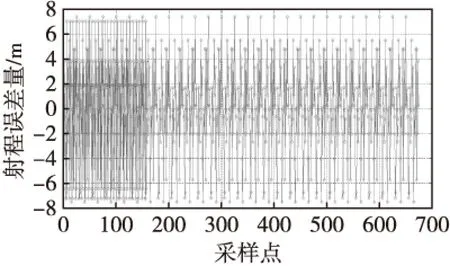
图2 射程预测误差量Fig.2 Error of predicted range

图3 横偏预测误差量Fig.3 Error of predicted transverse rage

射角/(°)数值积分法BP神经网络PSO优化SVM射程/m横偏/m解算时间/ms射程/m横偏/m解算时间/ms射程/m横偏/m解算时间/ms4210961573.31526.210764554.86144.310955572.75419.14521966697.221467.522225719.17760.5421959696.333931.4488410173.95441.98296.7157.73135.578405.4173.51815.3

3.2.2 落点预报仿真结果分析

由表2可知，本文方法在落点预测精度与解算时间上均有很大的优势，满足解算精度和快速性的要求。也就是说当输入量为完备的(x,y,z,vx,vy,vz,θ,β)值时，在PSO优化SVM神经网络中很好地形成了由当前弹丸飞行状态信息到落点信息的非线性映射。

SVM神经网络的预测精度之所以有这样好的水准，其原因主要是由于SVM神经网络采用了不同于一般神经网络的经验风险最小化，而是采用结构风险最小化的原则。即将网络的训练误差作为优化问题的约束条件，而以置信区间为优化目标，同时兼顾了其学习能力和泛化能力。而不像一般神经网络那样存在学习能力和泛化能力的矛盾，即出现所谓“过拟合”问题。

实践表明，使用一般神经网络方法进行落点预报时，若神经网络输入层数据不完整，预报结果会产生较大误差。同时，因神经网络的性能依赖于训练样本，所以通用性不佳。

将离线训练得到的落点预报模型预先装入弹载计算机中，即PSO优化SVM神经网络落点预报模型在装入弹载计算机之前就已经训练完成。弹丸在飞行过程的某个时刻，利用载入的预报模型直接计算落点信息所用的时间，即为PSO优化SVM神经网络算法预报落点的时间，因而节省了大量的模型训练时间，使其满足快速解算的要求。

4 结论

为了快速高精确地实现弹丸落点预报，本文提出了基于PSO优化的SVM神经网络方法。该方法采用PSO优化算法优化SVM训练参数，以获得最优SVM神经网络预测模型。然后在此基础上，以某加农炮为例，使用经卡尔曼滤波处理后的数值积分法解算得到的6D自由度刚体外弹道数据，作为备选弹丸飞行状态数据。从射角6°到60°的范围内，每隔2°提取一条弹道数据，并在弹丸发射5s后每3s采集一次飞行弹道参数，直至飞行结束前5s结束采样，将这些弹道数据整合成神经网络的训练数据，进行了仿真。仿真结果表明:PSO的SVM神经网络逼近精度高，射程最大误差为7.371 8m，横偏最大误差为0.886 1m；收敛速度较快，比数值积分法快了一个数量级，比BP神经网络快了一倍。说明本文提出的方法对任意时刻弹丸飞行状态进行的落点预报是有效的，为弹丸落点预报的实际应用提供了一种参考。

[1]李志鹏,赵捍东,张帅，等.基于改进型BP神经网络的弹丸落点预测方法[J].弹箭与制导学报，2014,34(2): 75-78.

[2]黄鑫,赵捍东,李志鹏.基于插值型径向基神经网络的弹丸落点预报方法[J].探 测 与 控 制 学 报，2015,37(4):101-105.

[3]史金光,徐明友,王中原.卡尔曼滤波在弹道修正弹落点推算中的应用[J].弹道学报, 2008, 20(3):41-43.

[4]曹营军,朱宗平,李立春，等.基于BP人工神经网络的末修弹落点预测导引模式[J].弹箭与制导学报, 2011, 31(6):76-78.

[5]范磊,潘功配,欧阳的华，等.基于遗传算法结合支持向量机的Mg/PTFE贫氧推进剂配方优化[J].推进技术，2012,33(4):620-624.

[6]史峰,王小川,郁磊，等.MATLAB神经网络43个案例分析[M].北京：北京航空航天大学出版社,2010.

[7]刘伟,王建平,刘长虹，等.基于粒子群寻优的支持向量机番茄红素含量预测[J].农业机械学报，2012，43(4)：143-147.

[8]吴良海.基于粒子群优化支持向量机的石油需求预测[J].计算机仿真，2010，27(4):292-295.

[9]范磊,潘功配,欧阳的华，等.基于支持向量机的Mg/PTFE烟火药燃烧特性预测[J].含能材料，2012,20(4):414-417.

[10]徐明友.高等外弹道学[M].北京:高等教育出版社,2003:46-57．

[11]VISHALCR,YAAKOVBS,PETERW.Projectileidentificationandimpactpointprediction[J].IEEETransactionsonAerospaceandElectronicSystems,2010,46(4):2004-2021.

[12]KRAMERKA,STUBBERUDSC.ImpactTimeandPointPredictedUsingaNeuralExtendedKalmanFilter[C]//Proceedingsofthe2005IntelligentSensors,SensorNetworksandInformationProcessingConference.Melboume:IEEE,2005.

Impact-point Prediction Based on Particle Swarm OptimizationSVM Neural Network

MA Yan, ZHAN Handong, HUANG Xin

(College of Mechatronics Engineering, North University of China, Taiyuan 030051, China)

Aiming at the problem of the shortage of predicting a projectile impact-point quickly and precisely ,this paper introduced the forecasting method based on Particle Swarm Optimization support vector machine neural network.In order to obtain the optimal support vector machine neural network prediction model of impact-point, particle swarm optimization algorithm is used to optimize the training parameters of support vector machine.And then ,integrated the exterior ballistic data using the Kalman filtering into the training data of neural network for the impact-point prediction simulation test.Simulation results show that the maximum range error of the method is 7.371m, and the maximum partial navigation error is 0.886m; The forecast time of impact-point is within 35ms which is faster than the numerical integration method in an order of magnitude.Therefore, this method provides a road for the practical application of the projectile impact point prediction.

neural network;particle swarm optimization algorithm;support vector machine;impact-point prediction.

2016-12-13

马焱(1991—)，男，湖北黄冈人，硕士研究生，研究方向：弹箭飞行控制。E-mail:1780942802@qq.com。

K875.8

A

1008-1194(2017)02-0124-05