(λ，μ)-模糊商环及其同构定理①

张蒙蒙 尹玉祥

(聊城大学数学科学学院，山东聊城252059)

(λ，μ)-模糊商环及其同构定理①

张蒙蒙 尹玉祥

(聊城大学数学科学学院，山东聊城252059)

在(λ，μ)-模糊子环与(λ，μ)-模糊理想概念的基础上，讨论了(λ，μ)-模糊商环与(λ，μ)-商模糊子环的若干性质，最后建立了(λ，μ)-模糊商环的同构定理.

λ，μ)-模糊子环;(λ，μ)-模糊理想;(λ，μ)-模糊商环;(λ，μ)-商模糊子环;同构定理

0 引言

1965年，Zadeh首次提出模糊集概念，创立了模糊集合论，并在此基础上形成了模糊数学这门新学科[1].1971年，Rosenfeld 将模糊集理论应用到群上，提出了模糊群的概念，形成了模糊代数学[2]. 随着代数结构的模糊化， 大批学者将模糊集理论应用到环和模上，先后提出了模糊子环、模糊理想、(λ，μ)-模糊子环、(λ，μ)-模糊理想等概念. 2008年，姚炳学所著的关于群与环上的模糊理论的书，详细地介绍了群与环的模糊理论和代数结构提升理论[3]. 本文是在(λ，μ)-模糊子环和(λ，μ)-模糊理想意义下[4]，利用(λ，μ)-模糊商环的性质，建立了(λ，μ)-模糊商环及其同构理论，进一步丰富了(λ，μ)-模糊子环的内容.

1 预备知识

在本文中，R表示一个环，λ,μ满足0≤λ<μ≤1.

定义1[4]设A为环R的模糊子集，称A为R的(λ，μ)-模糊子环，如果对任意的x,y∈R，

1)A(x+y)∨λ≥(A(x)∧A(y))∧μ;2)A(-x)∨λ≥A(x)∧μ;3)A(xy)∨λ≥(A(x)∧A(y))∧μ.

根据上述定义，普通的模糊子环是(0,1)模糊子环，而(∈,∈∨q)模糊子环是(0,0.5)模糊子环.

定理1[4]设A为环R的模糊子集，则A为R的(λ，μ)-模糊子环的充分必要条件是∀x,y∈R,

1)A(x-y)∨λ≥(A(x)∧A(y))∧μ;

2)A(xy)∨λ≥(A(x)∧A(y))∧μ.

定理2[4]设A为R的(λ，μ)-模糊子环，则对任意的x∈R,A(0)∨λ≥A(x)∧μ特别地，若存在x0∈R,使得A(x0)≥μ则A(0)≥μ.

由此显然可得，若A为R的(λ，μ)-模糊子环，则对任意的x∈R,A(0)∨λ∧μ≥A(x)∨λ∧μ.

定义2[4]设A为环R的模糊子集，称A为R的(λ，μ)-模糊理想，如果对任意的x,y∈R，

1)A(x-y)∨λ≥(A(x)∧A(y))∧μ;

2)A(xy)∨λ≥(A(x)∨A(y))∧μ.

定理3[3]设f：R1→R2为环的同态映射，且A为R1的(λ，μ)-模糊子环，则f(A)为R2的(λ，μ)-模糊子环.特别地，若f为同态满射且A为R1的(λ，μ)-模糊理想，则f(A)为R2的(λ，μ)-模糊理想.

定理4[3]设f：R1→R2为环的同态映射，B为R2的(λ，μ)-模糊子环((λ，μ)-模糊理想)，则f-1(B)为R1的(λ，μ)-模糊子环((λ，μ)-模糊理想).

定理5[3]设A为R的(λ，μ)-模糊子环，a,b∈R，则

(A(a-b)∨λ)∧μ=(A(0)∨λ)∧μ⟺(A(b-a)∨λ)∧μ=(A(0)∨λ)∧μ.

2 (λ，μ)-模糊商环与(λ，μ)-商模糊子环

设A为R的(λ，μ)-模糊子环，对任意的r∈R，定义R的模糊子集r⊕A如下：

(r⊕A)(x)(A(x-r)∨λ)∧μ,∀x∈R.

定义3[3]设A为R的(λ，μ)-模糊理想，则(R/A,+○,)做成环，其中，R/A={a⊕A|a∈R}(x⊕A)+(y⊕A)(x+y)⊕A,(x⊕A)○(y⊕A)xy⊕A.

并称(R/A,+○,)为R关于A的(λ，μ)-模糊商环.

定理6[3]设A为R的(λ，μ)-模糊子环，a,b∈R,则a⊕A=b⊕A⟺(A(a-b)∨λ)∧μ=(A(0)∨λ)∧μ.

定理7[3]设A为R的(λ，μ)-模糊理想，则对任意的x,y,a,b∈R,

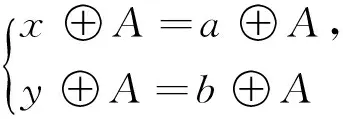
定理8 设A,B分别为R的(λ，μ)-模糊理想与(λ，μ)-模糊子环，则B/A为R/A的(λ，μ)-模糊子环，其中,B/A(r⊕A)sup{B(x)|x⊕A=r⊕A},∀r∈R.

证明 ∀x,y∈R,B/A((x⊕A)-(y⊕A))∨λ

=B/A((x-y)⊕A)∨λ

=sup{B(u-v)|(u-v)⊕A=(x-y)⊕A}∨λ

=sup{B(u-v)∨λ|(u-v)⊕A=(x-y)⊕A}

≥sup{B(u)∧B(v)∧μ|u⊕A=x⊕A,v⊕A=y⊕A}

=sup{B(u)|u⊕A=x⊕A}∧sup{B(v)|v⊕A=y⊕A}∧μ

=B/A(x⊕A)∧B/A(y⊕A)∧μ.

同理，B/A((x⊕A)°(y⊕A))∨λ≥B/A(x⊕A)∧B/A(y⊕A)∧μ.因此，B/A为R/A的(λ，μ)-模糊子环.

类似地，有

定理9 设A,B为R的(λ，μ)-模糊理想，则B/A为R/A的(λ，μ)-模糊理想.

证明 由定理8，B/A为R/A的(λ，μ)-模糊子环.∀x,y∈R,

B/A((x⊕A)°(y⊕A))∨λ=B/A((xy)⊕A)∨λ

=sup{B(uv)|(uv)⊕A=(xy)⊕A}∨λ

=sup{B(uv)∨λ|(uv)⊕A=(xy)⊕A}

≥sup{B(u)∨B(v)∧μ|u⊕A=x⊕A,v⊕A=y⊕A}

=sup{B(u)|u⊕A=x⊕A}∨sup{B(v)|v⊕A=y⊕A}∧μ

=B/A(x⊕A)∨B/A(y⊕A)∧μ，

所以，B/A为R/A的(λ，μ)-模糊理想.

定义4[3]设A,B分别为R的(λ，μ)-模糊理想与(λ，μ)-模糊子环，则B/A为R/A的(λ，μ)-模糊子环，B/A称为B关于A的(λ，μ)-商模糊子环.

定理10[3]设A为R的(λ，μ)-模糊理想，则R/A#≅R/A,其中，

A#={x∈R|(A(x)∨λ)∧μ=(A(0)∨λ)∧μ}.

3 (λ，μ)-模糊商环的同构定理

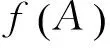
定理11[3]设f：R1→R2为同态满射，A为R1的关于f不变的(λ，μ)-模糊理想，则R1/A≅R2/f(A).

推论1[3]设f：R1→R2为同态满射，B为R2的(λ，μ)-模糊理想，则R1/f-1(B)≅R2/B.

定理12 设A,B分别为R的(λ，μ)-模糊子环与(λ，μ)-模糊理想，则A≈A/B.

证明 令f:R→A/B,F|→F⊕B为自然同态，则f为同态满射. ∀x∈R,

f(A)(x⊕B)=sup{A(t)|f(t)=x⊕B}

=sup{A(t)|t⊕B=x⊕B}=A/B(x⊕B),

即f(A)=A/B, 所以A≈A/B.

定理13 设f：R1→R2为环的同态满射，A,B分别为R1的(λ，μ)-模糊子环与(λ，μ)-模糊理想，若B为f不变的，则A/B≅f(A)/f(B).

证明 由定理11，g:R1/B→R2/f(B),x⊕B|→f(x)⊕f(B),∀x∈R1是一个同构映射. ∀y∈R2,∃x∈R1,使得f(x)=y，所以

f(A)/f(B)(y⊕f(B))=f(A)/f(B)(f(x)⊕f(B))

=sup{f(A)(v)|v⊕f(B)=f(x)⊕f(B)}

=sup{sup{A(u)|f(u)=v}|v⊕f(B)=f(x)⊕f(B)}

=sup{A(u)|f(u)⊕f(B)=f(x)⊕f(B)}

=sup{A(u)|(f(B)(f(x)-f(u))∨λ)∧μ=(f(B)(02)∨λ)∧μ}

=sup{A(u)|(B(x-u)∨λ)∧μ=(B(02)∨λ)∧μ}

=sup{A(u)|u⊕B=x⊕B}

=A/B(x⊕B)

=g-1(g(A/B))(x⊕B)

=g(A/B)(g(x⊕B))

=g(A/B)(f(x)⊕f(B))

=g(A/B)(y⊕f(B)),

即g(A/B)=f(A)/f(B). 因此A/B≅f(A)/f(B).

推论2 设f：R1→R2为环的同态满射，A,B分别为R2的(λ，μ)-模糊子环与(λ，μ)-模糊理想, 则f-1(A)/f-1(B)≅A/B.

证明 易知f-1(A)与f-1(B)分别为R1的(λ，μ)-模糊子环与(λ，μ)-模糊理想,对任意的x1,x2∈R2,由f(x1)=f(x2)可得

f-1(A)(x1)=A(f(x1))=A(f(x2))=f-1(A)(x2),

f-1(B)(x1)=B(f(x1))=B(f(x2))=f-1(B)(x2),

所以f-1(A)与f-1(B)是f不变的，f是满射，所以f(f-1(A))=A,f(f-1(B))=B.由定理13，f-1(A)/f-1(B)≅A/B.

引理1 设A,B为R的(λ，μ)-模糊理想，且满足A⊇B,A(0)∨λ∧μ=B(0)∨λ∧μ， 则∀x,y∈R,x⊕B⊕A/B=y⊕B⊕A/B⟺x⊕A=y⊕A.

证明 必要性. 设x⊕B⊕A/B=y⊕B⊕A/B，则

(A/B)((x-y)⊕B)∨λ∧μ=(A/B)(B)∨λ∧μ=A(0)∨λ∧μ,

从而sup{A(t)|t⊕B=(x-y)⊕B}∨λ∧μ=sup{A(t)∨λ∧μ|t⊕B=(x-y)⊕B}=A(0)∨λ∧μ

若t⊕B=(x-y)⊕B，则B(x-y-t)∨λ∧μ=B(0)∨λ∧μ，于是

A(x-y)∨λ∧μ≥(A(x-y-t)∧A(t))∨λ∧μ

≥(B(x-y-t)∧A(t))∨λ∧μ

=(B(x-y-t)∨λ∧μ)∧(A(t)∨λ∧μ)

=(B(0)∨λ∧μ)∧(A(t)∨λ∧μ)

=(B(0)∧A(t))∨λ∧μ

=A(t)∨λ∧μ,

故A(x-y)∨λ∧μ≥sup{A(t)∨λ∧μ|t⊕B=(x-y)⊕B}=A(0)∨λ∧μ，

又A(0)∨λ∧μ≥A(x-y)∨λ∧μ，从而x⊕A=y⊕A.

充分性. 设x⊕A=y⊕A. 则A(x-y)∨λ∧μ=A(0)∨λ∧μ=(A/B)(B)∨λ∧μ,

于是(A/B)((x-y)⊕B)∨λ∧μ=sup{A(t)|t⊕B=(x-y)⊕B}∨λ∧μ=A(0)∨λ∧μ=A(x-y)∨λ∧μ=(A/B)(B)∨λ∧μ,又(A/B)(B)∨λ∧μ≥(A/B)((x-y)⊕B)∨λ∧μ，故(A/B)(B)∨λ∧μ=(A/B)((x-y)⊕B)∨λ∧μ=(A/B)((x⊕B)-(y⊕B))∨λ∧μ，所以x⊕B⊕A/B=y⊕B⊕A/B.

定理14 设A,B为R的(λ，μ)-模糊理想，且满足A⊇B,A(0)∨λ∧μ=B(0)∨λ∧μ， 若C为R的(λ，μ)-模糊子环，则(C/B)/(A/B)≅C/A.

证明 令f:(R/B)/(A/B)→R/A,r⊕B⊕A/B|→r⊕A,∀r∈R,则由引理1，f为单射，而且显然也是满射. 又∀x,y∈R,

f((x⊕B⊕A/B)+(y⊕B⊕A/B))=f(x⊕y⊕B⊕A/B)=x⊕y⊕A=(x⊕A)+(y⊕A),

f((x⊕B⊕A/B)°(y⊕B⊕A/B))=f(xy⊕B⊕A/B)=xy⊕A=(x⊕A)°(y⊕A),

所以f为同构映射. 又

((C/B)/(A/B))(x⊕B⊕A/B)=sup{C/B(r⊕B)|r⊕B⊕A/B=x⊕B⊕A/B}

=sup{sup{C(u)|u⊕B=r⊕B}|r⊕B⊕A/B=x⊕B⊕A/B}

=sup{C/B(r⊕B)|r⊕B⊕A/B=x⊕B⊕A/B}

=sup{C(u)|u⊕B⊕A/B=x⊕B⊕A/B}

=sup{C(u)|u⊕A=x⊕A}

=C/A(x⊕A)=C/A(f(x⊕B⊕A/B))

=f-1(C/A)(x⊕B⊕A/B),

即 (C/B)/(A/B)=f-1(C/A), 从而f((C/B)/(A/B))=C/A, 因此(C/B)/(A/B)≅C/A.

4 结束语

本文将模糊商环和商模糊子环推广到(λ，μ)-模糊商环和(λ，μ)-商模糊子环，并类比(λ，μ)-模糊商群的同构定理建立了(λ，μ)-模糊商环的同构定理,进一步丰富了模糊环理论.

[1] Zadeh L A. Fuzzy sets[J]. Inform and Control, 1965, 8(1): 338-353.

[2] Rosenfeld A. Fuzzy groups[J]. Math Anal Appl, 1971, 35: 512-517.

[3] 姚炳学. 群与环上的模糊理论[M]. 北京：科学出版社，2008.

[4] Yao B.(λ，μ)-fuzzy subrings and(λ，μ)-fuzzy ideals[J]. The Journal of Fuzzy Mathematics, 2007, 15(4): 981-987.

[5] Kumbhojkar H V, Bapat M S. Correspondence theorem for fuzzy ideals[J]. Fuzzy Sets and Systems, 1991, 41: 213-219.

[6] Yao B, Li Y, Shi K. Isomorphism theorems of generalized fuzzy quotient rings[J]. The Journal of Fuzzy Mathematics, 2003, 11(4): 827-833.

[7] 郝翠霞，姚炳学.(λ，μ)-商模糊子群及其同构定理[J]. 模糊系统与数学，2015, 29(1): 35-42.

(λ，μ)-Fuzzy Quotient Ring and Isomorphism Theorem

ZHANG Meng-meng YIN Yu-xiang

(School of Mathematical Sciences, Liaocheng University, Liaocheng 252059, China)

Based on the concept of(λ，μ)-fuzzy subring and(λ，μ)-fuzzy ideal, seveal properties of(λ，μ)-fuzzy quotient ring and(λ，μ)-quotient fuzzy subring were discussed. Finally, the isomorphism theorems for(λ，μ)-fuzzy quotient rings were established.

(λ，μ)-fuzzy subring， (λ，μ)-fuzzy ideal， (λ，μ)-fuzzy quotient ring， (λ，μ)-quotient fuzzy subring， isomorphism theorems

2016-10-15

国家自然科学基金项目(11471152)资助

张蒙蒙，E-mail:1833448183@qq.com.

O153

A

1672-6634(2017)01-0018-04