带外挂机翼颤振分析的传递函数方法

段静波， 江 涛

(1. 西北工业大学 航空学院， 西安 710072；2. 军械工程学院 无人机工程系， 石家庄 050003)

带外挂机翼颤振分析的传递函数方法

段静波1,2， 江 涛2

(1. 西北工业大学 航空学院， 西安 710072；2. 军械工程学院 无人机工程系， 石家庄 050003)

将传递函数方法应用于带外挂机翼的颤振分析。利用干净机翼的弯扭振动微分方程和Therdorson非定常气动力模型建立了机翼颤振方程。将外挂视为与机翼连接的具有质量及转动惯量的刚体，且考虑机翼与外挂间的俯仰联接刚度，通过变形协调和内力平衡等连接条件引入机翼颤振模型。运用传递函数方法，将颤振微分方程转换为状态空间形式，通过求解复特征值问题获得了带外挂机翼的颤振速度和颤振频率。通过与已有文献及有限元结果对比，验证了该方法的正确性和有效性。最后，讨论了外挂质量、转动惯量、外挂位置、挂架俯仰联接刚度等因素对带外挂机翼颤振特性的影响。

带外挂机翼；非定常气动力；颤振；传递函数法

机翼是飞机气动弹性分析的重要对象。通常机翼下会安装发动机、导弹等外挂，这将会显著改变机翼的颤振特性。某些外挂状态甚至可能导致颤振临界速度的急剧降低，严重影响飞机的安全性。因此，对带外挂机翼颤振问题一直是飞机设计中受到广泛重视的课题。国内外学者在此方面进行了诸多研究。20世纪90年代，杨智春等[1]就采用颤振分析重频理论对带外挂物二元机翼的颤振频率及颤振边界变化的一般规律进行了研究，并进行了实验验证。杨智春等[2-3]还建立实验模型研究俯仰、偏航、侧摆等联接刚度对机翼/外挂系统颤振特性的影响。Yang[4]应用KBM方法的一次、二次近似理论研究了机翼外挂系统以及三角机翼两种模型的极限环颤振。杨翊仁等[5]按照工程处理的思路，先用一阶谐波平衡当量线化方法估计系统极限环颤振频率，然后引用孤立外挂单自由度系统在简谐迫振情况下的次谐分叉频率条件来预估机翼带外挂系统极限环颤振的次谐响应存在区域。叶炜梁[6]根据颤振运动方程，应用v-g参数法和非定常气动力的偶极子格网法计算了CKI机翼翼尖带外挂物时的颤振特性。近年来，Ozcan等[7]采用实验和数值分析方法对带外挂机翼的气动特性进行了研究。Tang等[8]采用实验的方法对带外挂三角翼的颤振、极限环振荡在低速风洞中进行了研究，并与理论结果进行了对比分析。Fazelzadeh等[9]采用扩展伽辽金法研究了飞机滚转下带外挂机翼的分叉和颤振问题。Librescu等[10]采用扩展伽辽金法研究了复合材料带外挂机翼的气动弹性稳定性及响应问题。Karpel等[11]提出一种新的模态耦合技术，可以高效地进行带外挂机翼的颤振及气动伺服弹性分析。邱志平等[12]、Tang等[13]分别研究了带有间隙型非线性刚度的带外挂机翼的颤振问题。Chen等[14]提出了一种基于谐波平衡法的增量法来研究带外挂翼型的极限环颤振问题，并将该问题转化为极值问题求解。许军等[15]基于Hamilton原理推导带外挂机翼的动力学方程，研究了大展弦比带外挂机翼弯弯扭运动的颤振特性。王钢林等[16]采用梁单元对双梁式机翼和发动机吊舱进行了结构建模，研究了机翼在不同攻角时的定常气动力及发动机推力联合作用下固有振动和颤振特性的变化情况。

传递函数方法是一种基于控制理论的半解析计算方法。该方法求解过程简洁和统一，边界条件处理规范和方便，常用于动力学系统的稳定性、动态响应特性分析。Yang[17]最早提出了该方法，并应用于梁、杆等一维结构振动问题。周建平等[18-19]系统地将方法拓展应用于平面应力问题、薄板弯曲问题、厚壁圆柱壳和加筋柱壳等二维、三维的结构振动问题。之后，冯莹等[20]将传递函数方法应用于光波导传播特性分析。李恩奇[21]基于分布参数传递函数方法进行了被动约束层阻尼结构的动力学分析。赵雪川[22]将传递函数方法应用于非局部弹性和黏弹性结构的动力学分析。Shen等[23]等基于传递函数方法研究了碳纳米管的力学问题。由于机翼颤振本质上也是系统动力学稳定性问题，因而，本文在前人研究的基础上，将传递函数方法应用于带外挂机翼的颤振分析。

1 颤振分析模型

1.1 机翼弯扭振动微分方程

图1所示为一根长直机翼，其半展长为L，半弦长为b。取固支端与机翼刚轴的交点为原点建立坐标系，y轴沿机翼轴线从翼根指向翼梢，x轴沿机翼弦向由前缘指向后缘，与y轴正交，z轴与x，y轴构成右手系。在此坐标系下，机翼的弯扭振动微分方程可写为

(1)

式中，h为机翼弯曲振动位移，α为机翼扭转振动转角，EI为机翼抗弯刚度，GJ为机翼抗扭刚度，m为机翼单位长度质量，Iα为单位长度机翼绕弹性轴的转动惯量，xα为机翼弹性轴到机翼截面重心的距离，Lh为机翼单位长度的升力，Tα机翼单位长度的扭矩，y为机翼展向坐标，t为时间。

(a)机翼展向

(b)机翼剖面图1 长直机翼示意图Fig.1 A straight aircraft wing

1.2 非定常气动力模型

在忽略机翼重力影响条件下，机翼颤振时的外力只有气动力。本文采用片条理论进行非定常气动力计算。根据Theodorson理论，单位展长的非定常升力与相应的俯仰力矩按下式计算[24]

(2)

由于减缩频率k是圆频率ω和空速v的函数，为了后续求解方便 ，将C(k)写为C(ω,v)，其它符号含义同文献[24]。将式(2)代入式(1)得到机翼颤振微分方程

(3)

1.3 机翼挂载的处理

在处理机翼挂载时，考虑外挂的质量惯量特性，以及与机翼间的俯仰联接刚度，而且忽略外挂俯仰运动产生的铅垂方向(图1中z轴方向)的位移，忽略外挂气动力对机翼颤振的影响。

对干净机翼而言，将机翼可视为一根悬臂梁，其边界变形协调条件和内力平衡条件为

(4)

当机翼存在挂载时，设沿机翼轴线方向上距翼根y0处存在一个外挂，外挂质量为m0，转动惯量记I0，外挂距机翼弹性轴的距离为x0，β(t)为外挂相对翼根弦线的俯仰扭转角，Kβ为挂架俯仰扭转刚度，如图2所示。在求解带外挂机翼颤振问题时，以外挂为界，将机翼分为左右两部分，中间通过变形协调条件和内力平衡条件联系两部分。为进行区分，外挂左侧机翼所有物理量增加下标“1”，外挂右侧机翼所有物理量增加下标“2”。

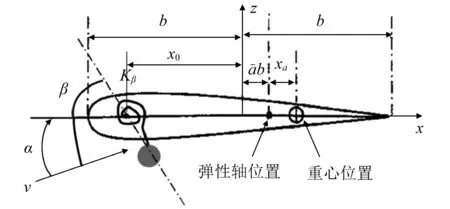
图2 外挂处机翼剖面示意图Fig.2 Wing section on the position of the external store

基于机翼弯扭振动模型，在外挂处机翼变形应满足弯曲挠度、弯曲转角及扭转角三方面的变形协调条件，具体为

(5)

同时，在挂载处机翼内力应满足弯矩、剪力及扭矩三方面的内力平衡条件，具体为

(6)

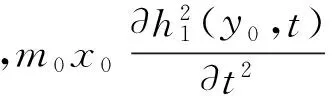
上述边界条件中引入了一个新自由度β(t)，因而需要补充一个条件。对于外挂，其俯仰振动微分方程为

(7)

2 传递函数法求解

对机翼颤振微分方程式(3)进行Fourier变换，并整理可得

(8)

式中，A1(ω,v)、A2(ω,v)、B1(ω,v)、B2(ω,v)的具体表达式如下

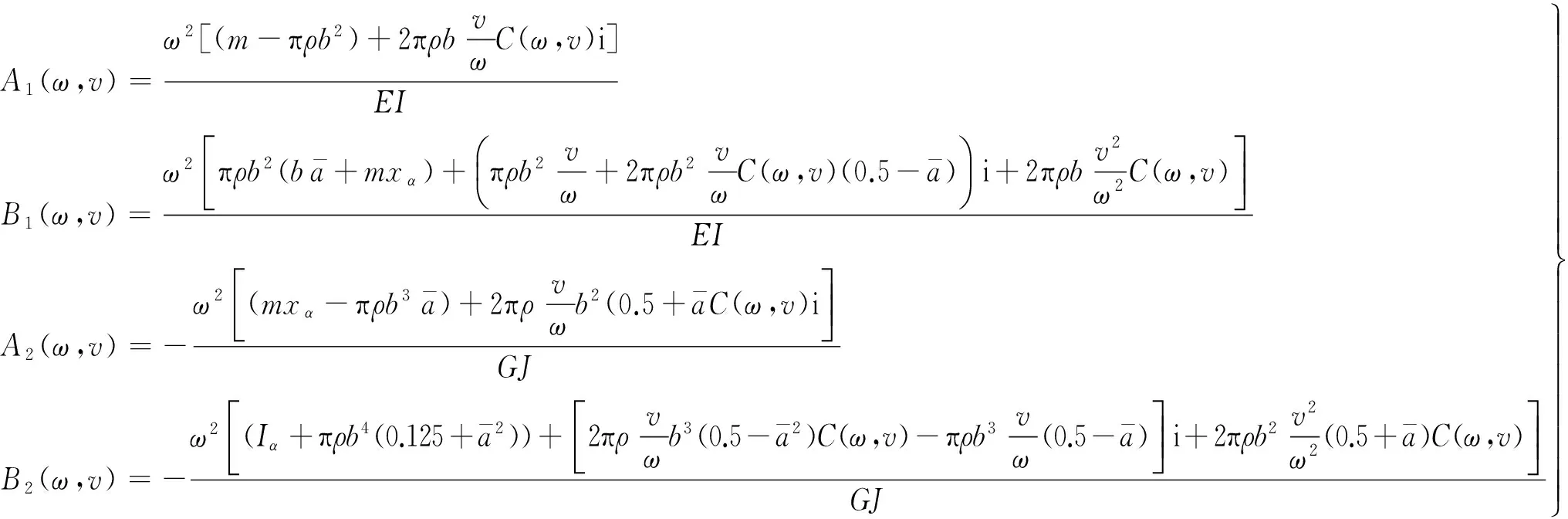
(9)

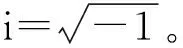
根据传递函数方法，定义状态变量向量如下

(10)

式中，T表示向量转置。

从而，式(8)可写成如下状态空间方程的形式：

(11)

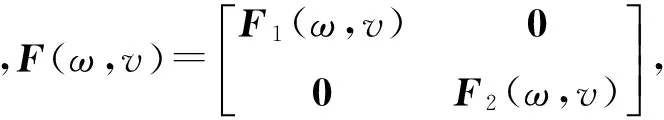
(i=1,2)。

由于式(8)为齐次微分方程组，因而式(11)

中g(ζ,ω)=0。

根据传递函数方法，带外挂机翼边界与外挂处的变形协调条件、内力平衡条件可以写为矩阵形式

Mbη(y=0,ω)+Nbη(y=L,ω)+
R0η(y=y0,ω)=γ(ω)

(12)

式中，Mb为机翼根端边界条件选择矩阵，Nb为机翼梢端边界条件选择矩阵，由于机翼根端固支梢端自由，因而，Mb、Nb的表达式可写为

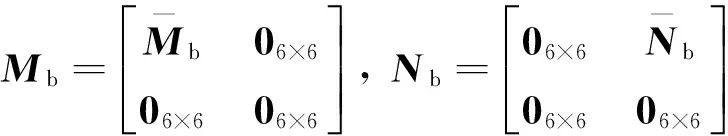
R0为机翼外挂处连续条件选择矩阵，联立式(5)、式(6)、式(7)可得出其表达式

将Mb、Nb、R0的矩阵式代入式(12)，且根据机翼两端边界条件式(4)，可得到

(13)

根据传递函数理论，式(11)的解可写为

(14)

式中，G(y,ζ,ω,v)为状态空间方程的域内传递函数，H(y,ω,v)为状态空间方程的边界传递函数，其表达式分别为

(15)

式中，变量ζ∈(0,L)，为机翼展向的坐标。

因为g(ζ,ω)=0且γ(ω)=0，由式(14)可进一步得到

(16)

当机翼颤振时，弯曲振动位移h和扭转振动转角α的振幅为非零常数，即式(16)的η(y,ω)有非零解，则有：

(17)

令：

(18)

由于A为复矩阵，其行列式值等于零的必要条件为矩阵行列式值的实部与虚部均为零，即

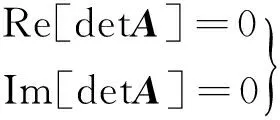
(19)

矩阵A中有空速v和圆频率ω两个变量，而式(19)恰好有两个方程，可以定解。求解上述式(19)，可能会得到满足方程式(19)的解，即存在多组(v,ω)能满足方程式(19)。根据机翼颤振时在某一空速时由稳定转变为不稳定，因而，空速v最小的一组解(v,ω)应为机翼的颤振速度和相应的颤振频率。

具体求解过程如下：

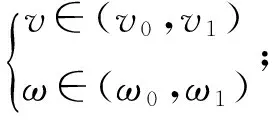
(j=0,1,2,3,...)；

步骤(3) 取空速v=v0，圆频率ω依次取，ω0+j△ω(j=0,1,2,3,...)将空速v和圆频率ω的取值及机翼各物理参数代入式(9)，得到系数A1(ω,v)、A2(ω,v)、B1(ω,v)、B2(ω,v)的值；

步骤(4) 利用系数A1(ω,v)、A2(ω,v)、B1(ω,v)、B2(ω,v)计算式(11)中矩阵F(ω,v)的值；

步骤(5) 利用机翼外挂参数计算矩阵R0；

步骤(6) 将矩阵F(ω,v)、Mb、Nb、R0的值代入式(18)，计算Re[detA]和Im[detA]的值；

步骤(7) 再依次取空速v=v0+j△v(j=1,2,3,...)，重复步骤(3)步骤(6)，计算Re[detA]和Im[detA]的值；

步骤(8) 确定满足式(19)的空速v和圆频率ω。

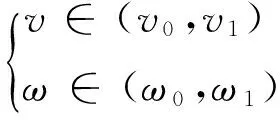
3 算例分析

3.1 正确性验证

机翼不携带外挂实际上是机翼外挂的质量和转动惯量退化零的情形。为了验证本文方法和代码的正确性，首先采用本文方法计算无外挂机翼的颤振特性。

文献[24]给出一无外挂机翼的颤振特性，机翼物理参数如表1所示，该机翼颤振的计算结果为：机翼颤振速度为35.3 m/s，颤振频率为24.0 Hz。文献[24]算例中机翼颤振频率单位为Hz，本文计算时只需将频率单位换算一下即可。

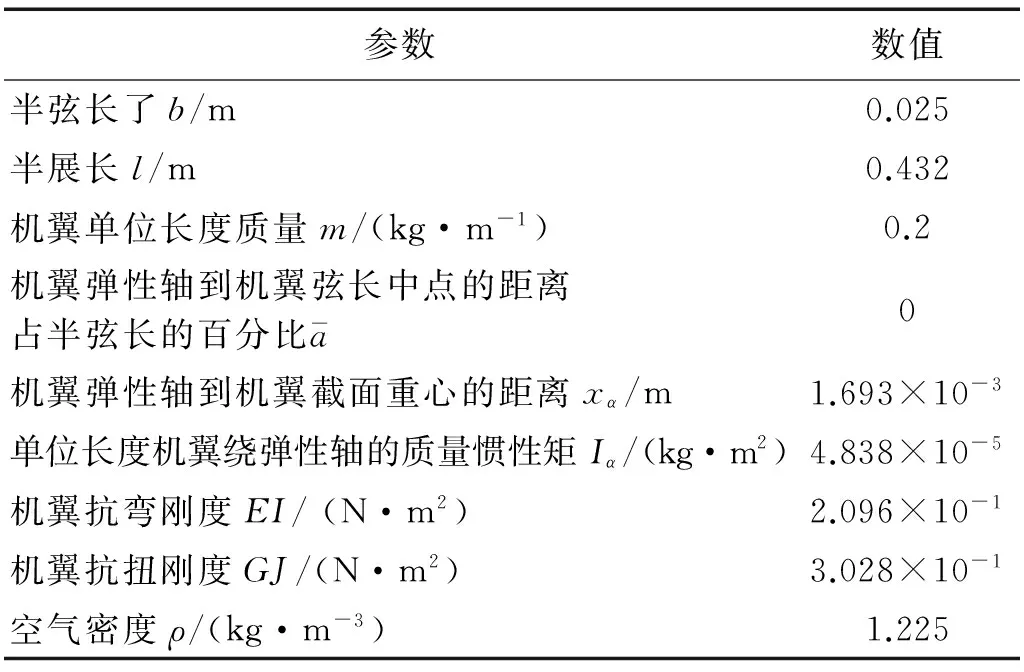
表1 机翼的物理参数

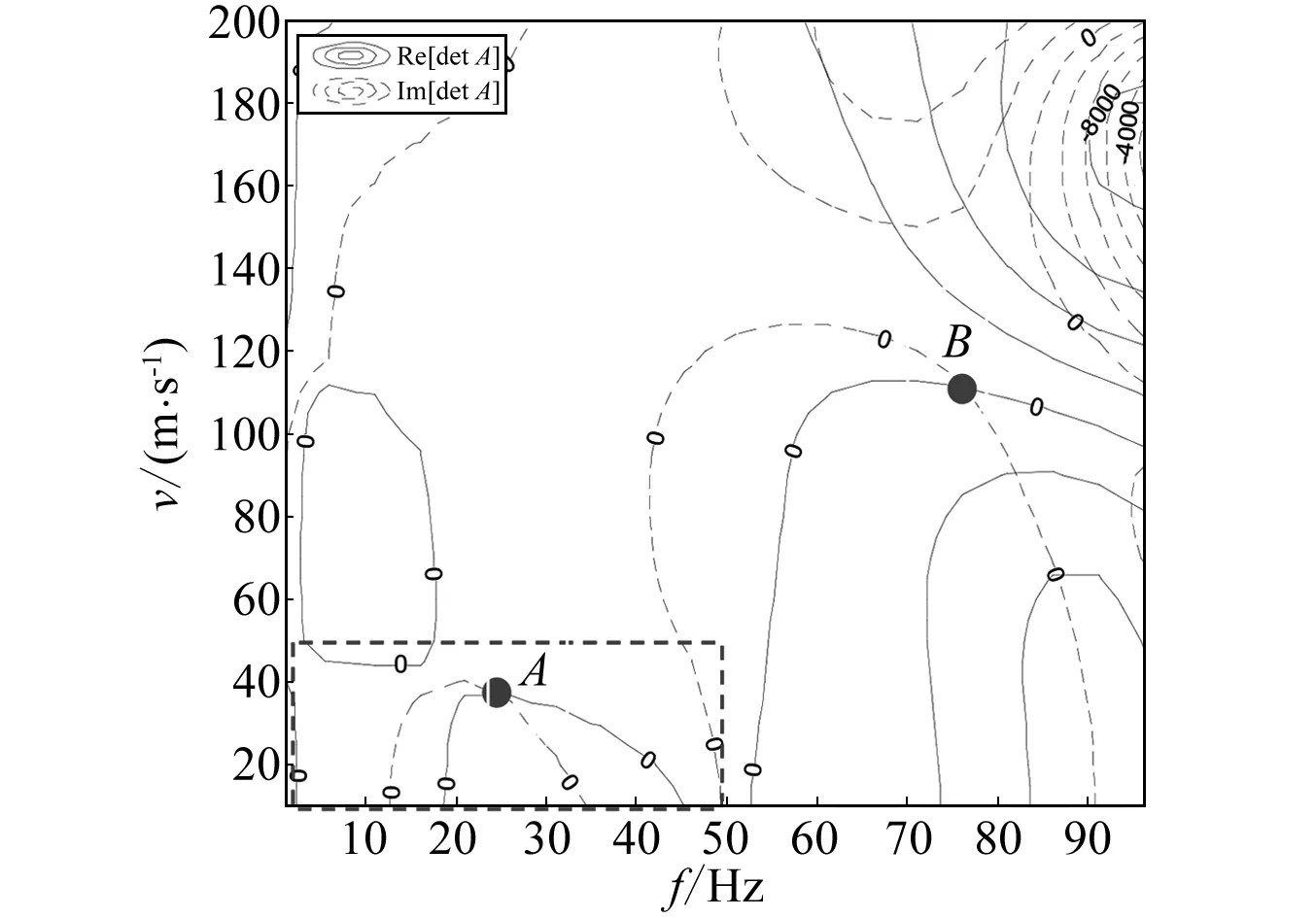
图3 和的等值线图Fig.3 The contour of Re[det A]and Im[det A]

图4 和的等值线图Fig.4 The contour of Re[det A]and Im[det A]

其次，采用本文方法计算机翼携带外挂的情形。外挂主要物理参数如表2所示。为了方便方法验证，设机翼重心到机翼弹性轴的距离xα=0，其它参数取表1中数据。在MSC.Patran中建立带外挂机翼有限元模型，如图5所示，采用壳单元，共划分40个单元，采用集中质量单元模拟机翼外挂的质量及转动惯量，并利用MSC.Nastran中的气动弹性分析模块MSC.FlightLoads进行气弹分析。

表2 外挂的物理参数

图5 带外挂机翼有限元模型Fig.5 The FEM model of the wing with an external store

表3给出了有无外挂情形下机翼固有特性的对比情况。从表3中可以看出，机翼外挂对机翼的固有特性会产生了影响，导致机翼弯曲、扭转固有频率均有了降低。特别是，外挂的出现使机翼的一阶扭转频率从38.03 Hz下降到了29.59 Hz。由于扭转特性对机翼颤振影响较大，这必将会导致机翼颤振特性的改变。表4给出了本文方法和有限元方法在机翼有无外挂情形下颤振特性的对比情况。从表4中可以看出，无论是机翼有外挂还是无外挂，两种方法得到的颤振速度与颤振频率比较吻合。由于MSC.FlightLoads进行气弹分析时，在结构方面进行了动力学降阶，利用了机翼若干低阶模态，模态的选用会影响结果的精度。在气动力模型方面MSC.FlightLoads采用的涡格法，能考虑机翼的三维效应；本文方法在结构方面直接采用微分方程，避免了模态降阶，但在气动力模型方面采用的是片条理论，不能考虑机翼的三维效应。因而，两种方法计算结果存在一定的差异。

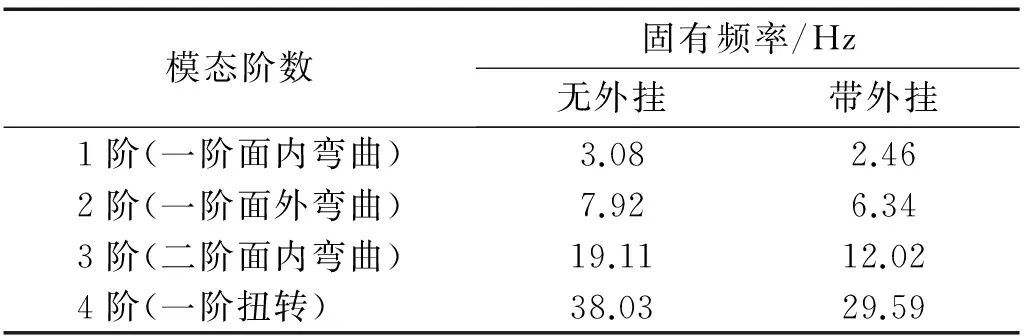
表3 机翼有无外挂固有频率对比

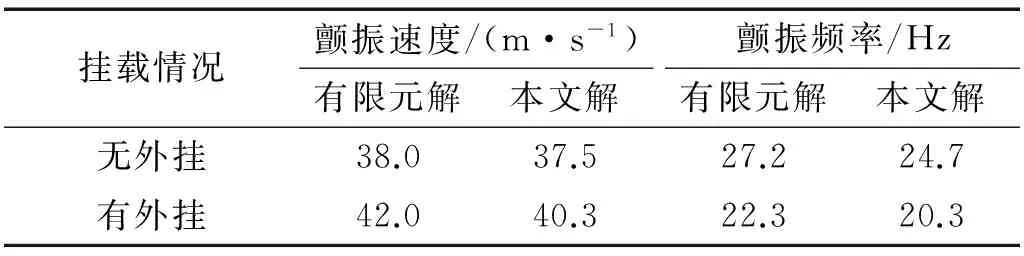
表4 机翼有无外挂颤振特性对比

3.2 外挂对机翼颤振特性的影响分析

从3.1节可知，带外挂机翼的颤振特性会随外挂特性变化而发生显著变化，因此有必要研究各种外挂参数对机翼颤振品质的影响。本节主要研究外挂质量、转动惯量、位置以及外挂与机翼间的联接刚度等因素对机翼颤振特性的影响。分析中所取基本参数见表1和表2。

图6给出了外挂质量变化对机翼颤振特性的影响。图中横坐标为机翼外挂质量m0与机翼单位长度质量m的比值，纵坐标为机翼颤振速度。图7给出了外挂转动惯量变化对机翼颤振特性的影响情况。图中横坐标为机翼外挂转动惯量I0与机翼单位长度转动惯量Iα的比值，纵坐标也为机翼颤振速度。图6和图7中均给出了外挂距机翼弹性轴弦向距离x0=-40%b、0、40%b三种下的颤振速度。从两图可以看出，采用传递函数法得到的外挂质量、转动惯量对机翼颤振影响是符合常理的，这也表明传递函数方法应用于机翼颤振分析是可行有效的。

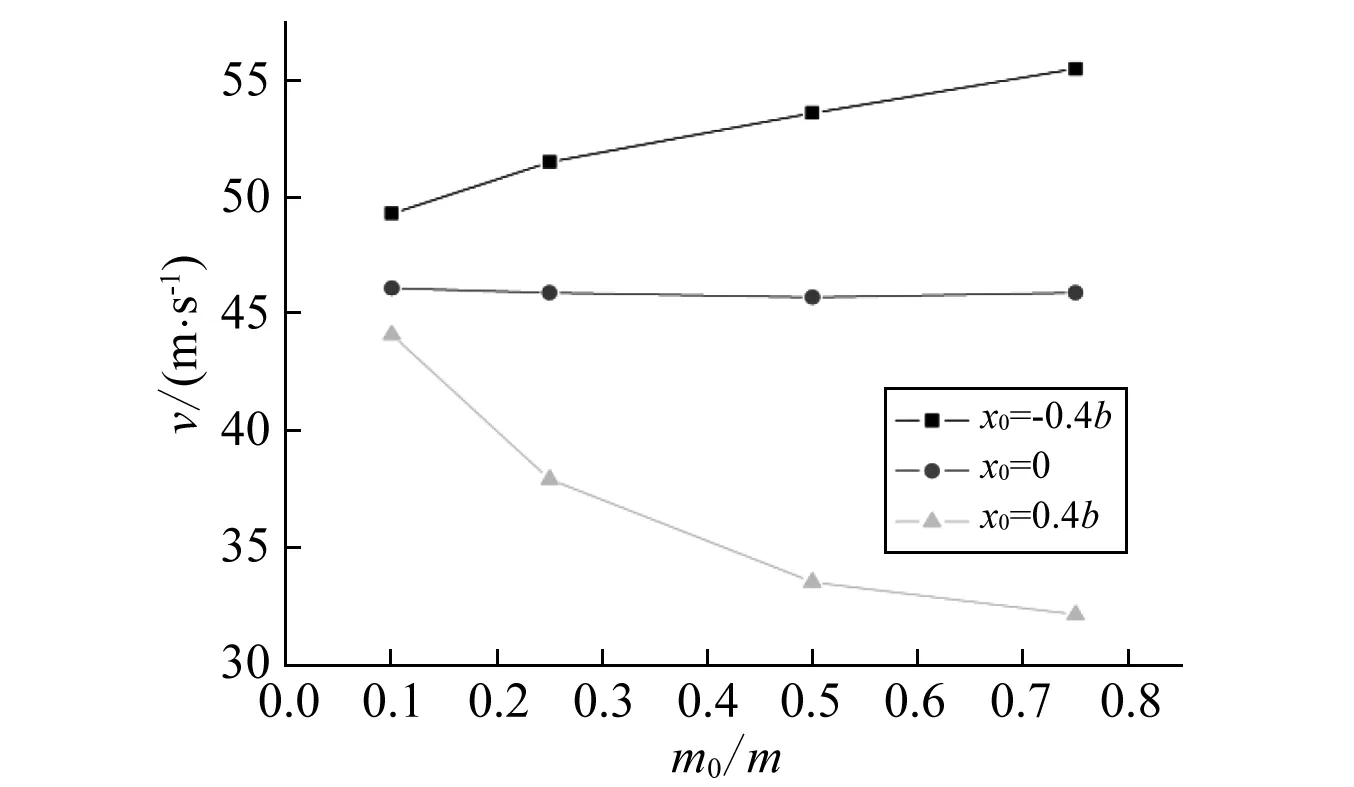
图6 机翼外挂质量对颤振速度的影响Fig.6 The influence of the mass of the external store on the velocity of the wing flutter

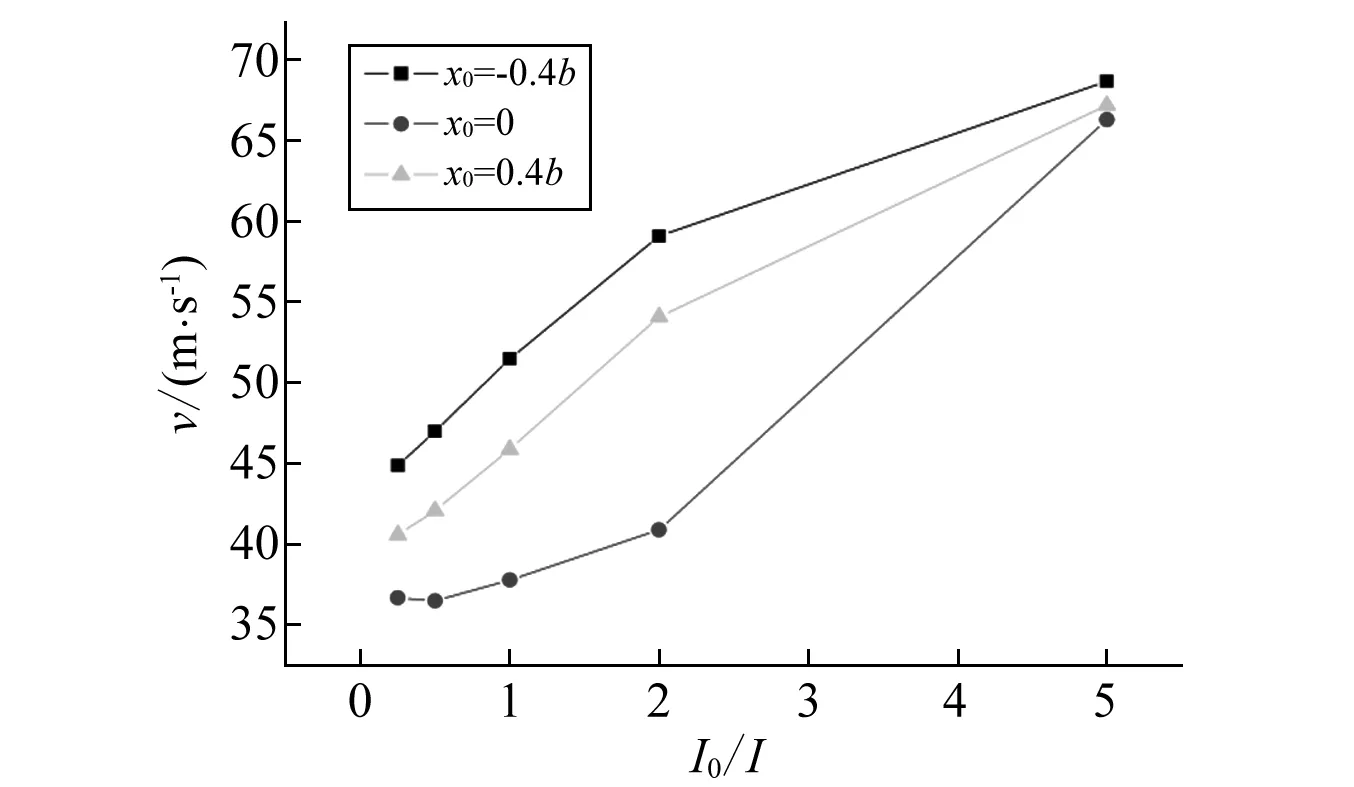
图7 机翼外挂转动惯量对颤振速度的影响Fig.7 The influence of the moment inertia of the external store on the velocity of the wing flutter

由于本文带外挂机翼颤振模型可以考虑机翼长度特性，因而本文给出了外挂在机翼展向上位置变化时对机翼颤振特性的影响，如图8所示。图上横坐标为机翼外挂展向位置y与机翼半展长L的比值，纵坐标为机翼颤振速度。从图中可以看出，随着外挂从翼根移向翼梢，当外挂在机翼弹性轴前时，机翼颤振速度是减小的，而当外挂位于机翼弹性轴上或位于机翼弹性轴后时，机翼颤振速度则是增大的。但是，外挂位于翼根翼中段时，仍然是外挂前于机翼弹性轴布置，有利于机翼颤振稳定性提高。然而，当外挂位于翼梢段时，外挂对机翼颤振速度的影响不再是这样了。从图8中虚线圆圈标注处可以看到，在三个弦向位置中，外挂位于x0=0处，机翼的颤振速度最大。这也就是说，外挂位于翼梢时，机翼可能会在弦向某位置出现颤振速度极大值。这与文献[6]中结论基本一致。因此，对于翼尖外挂，其弦向位置的确定就存在设计空间，需具体问题具体分析计算。

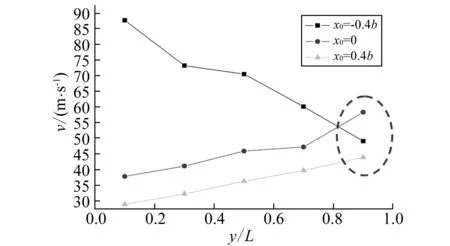
图8 外挂在机翼展向位置对颤振速度的影响Fig.8 The influence of the position of the external store on the velocity of the wing flutter

外挂挂架刚度也是机翼外挂的重要参数。因此，本文研究了外挂挂架俯仰刚度对机翼颤振的影响，如图9所示。图中横坐标为机翼外挂挂架俯仰刚度Kβ与机翼单位扭转刚度GJ的比值，纵坐标为机翼颤振速度。当GJ不变，Kβ改变时，从图中可以看出，当外挂挂架俯仰刚度Kβ较大时，对机翼颤振速度影响不大。但是，当外挂挂架俯仰刚度Kβ较小时，外挂挂架俯仰刚度对机翼颤振影响变得比较明显，在进行机翼设计时需要加以关注。

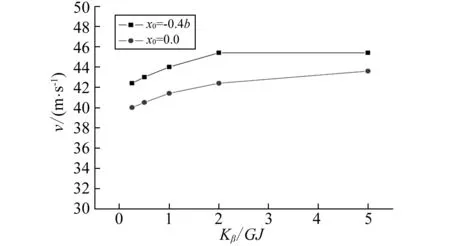
图9 外挂挂架俯仰刚度对颤振速度的影响Fig.9 The influence of pitch stiffness of the external-store pylons on the velocity of the wing flutter

4 结 论

(1)本文将传递函数方法应用于带外挂机翼颤振稳定性问题，通过本文结果与相关文献算例、MSC. FlightLoads结果对比验证，表明了本文方法的正确性和有效性；

(2)采用传递函数法处理机翼颤振问题时，在模型建立上，可以考虑机翼的长度特性，更近物理实际，有助于更好地揭示带外挂机翼的颤振机理；在计算过程中，该方法避免了动力学模型的降阶工作，而且能得到解析解，有助于提高求解效率；

(3)本文方法可以进一步拓展应用于质量、转动惯量、弦长等沿展向变化的更为普通的带外挂机翼颤振稳定性及气动弹性响应问题。

[1] 杨智春, 赵令诚. 带外挂二元机翼颤振模态的转变[J].航空学报，1992，13(9):A552-A554. YANG Zhichun, ZHAO Lingcheng. Transition of flutter mode of two-dimensional wing with external store[J]. Acta Aeronautica et Astronautica Sinica, 1992,13(9):A552-A554.

[2] 杨智春, 赵令诚. 联接刚度对机翼/外挂系统颤振边界特性的影响[J].应用力学学报，1993,10(2):1-6. YANG Zhichun, ZHAO Lingcheng. The effective elastic moduli of inhomogeneous media with randomly distributed inclusions[J]. Chinese Journal of Applied Mechanics, 1993,10(2):1-6.

[3] 杨智春,赵令诚,李伶,等. 偏航、侧摆联接刚度对带外挂三角机翼颤振特性的影响[J].振动工程学报，1992,5(2): 168-172. YANG Zhichun, ZHAO Lingcheng, LI Ling,et al. Effects of pylon yaw and lateral stiffness on the flutter of a delta wing with external store[J]. Journal of Vibration Engineering, 1992,5(2): 168-172.

[4] YANG Y R. KBM method of analyzing limit cycle flutter of a wing with an external store and comparison with a wind-tunnel test[J]. Journal of Sound and Vibration, 1995,187(2): 271-280.

[5] 杨翊仁, 赵令诚. 二元机翼带外挂系统极限环颤振次谐响应分析[J].航空学报, 1992, 13(7): 410-415. YANG Yiren, ZHAO Lingcheng. Subharmonic response of the limit cycle flutter of wing-store system[J]. Acta Aeronautica et Astronautica Sinica, 1992, 13(7): 410-415.

[6] 叶炜梁. 带翼梢外挂的CKI机翼颤振分析[J].南京航空航天大学学报,1993,25(4): 554-560. YE Weiliang. Analysis for flutter of CK1 wing with tip external store[J]. Journal of Naijing University of Aeronautics & Astronautics, 1993,25(4)：554-560.

[7] OZCAN O, UNAL M F, ASLAN A R, et al. Aeroelastic chanracteristics of external store configurations at low speeds[J]. Journal of Aircraft, 2011, 32(1):161-171.

[8] TANG D, DOWELL E H. Flutter and limit-cycle-oscillations for a wing-store model with freeplay[J]. Journal of Aircraft, 2006, 43(2):487-503.

[9] FAZELZADEH S A, MARZOCCA P, RASHID E, et al. Effects of rolling maneuver on divergence and flutter of aircraft wing store[J]. Journal of Aircraft, 2010, 47(1):64-71.

[10] LIBRESCU L, SONG O. Dynamics of composite aircraft wings carrying external stores[J]. AIAA Journal, 2008,46(3): 568-578.

[11] KARPEL M, MOULIN B, ANGUITA L, et al. Flutter analysis of aircraft with external stores using modal coupling[J]. Journal of Aircraft, 2004, 47(4):892-901.

[12] 周秋萍,邱志平. 机翼带外挂系统极限环颤振的区间分析[J]. 航空学报, 2010,31(3): 514-518. ZHOU Qiuping, QIU Zhiping. Interval analysis for limit cycle flutter of a wing with an external store[J]. Acta Aeronautica et Astronautica Sinica, 2010,31(3): 514-518.

[13] TANG D, DOWELL E H. Aeroelastic analysis and experiment for wing/store model with stiction nonlinearity[J]. Journal of Aircraft, 2011, 48(5):1512-1530.

[14] CHEN Y M, LIU J K, MENG G. An incremental method for limit cycle oscillations of an airfoil with an external store[J]. International Journal of Non-linear Mechanics, 2012,47:75-83.

[15] 许军,马晓平. 带外挂机翼的极限环颤振分析[J]. 机械强度，2014,36(6) : 841-845. XU Jun, MA Xiaoping. Limit cycle flutter analysis of a wing with an extrnal store[J]. Journal of Mechanical Strength, 2014,36(6) : 841-845.

[16] 王钢林，谢长川.考虑翼吊发动机推力的机翼颤振分析[J].航空科学技术,2014,25(6):22-27. WANG Ganglin, XIE Changchuan. Flutter analysis with the thrust effects of engine under wing[J]. Aeronautical Secience & Technology,2014,25(6):22-27.

[17] YANG B. Transfer function of constrained/combined one dimensional contimious dynamic systems[J]. ASME Joumal of Sound and Vibration,1992,156(3):425-443.

[18] 周建平,雷勇军. 分布参数系统的传递函数方法[M]. 北京: 科学出版社, 2006.

[19] 雷勇军. 结构分析的分布参数传递函数方法[D].长沙:国防科技大学,1998.

[20] 冯莹, 李湘荣, 李海阳, 等. 扩散平面光波导的传递函数方法[J].光学学报,1999,19(1):50-56. FENG Ying, LI Xiangrong, LI Haiyang, et al. Tranfer function analysis of diffused planar optical waveguides[J]. Acta Optical Sinica, 1999,19(1):50-56.

[21] 李恩奇. 基于分布参数传递函数方法的被动约束层阻尼结构动力学分析[D].长沙:国防科学技术大学,2007

[22] 赵雪川. 非局部弹性和粘弹性结构元件的力学分析[D]. 长沙:国防科技大学,2006.

[23] SHEN Zhibin, LI Xianfang, SHENG Liping,et al. Transverse vibration of nanoyube-based micro-mass sensor via nonlocal Timoshenko beam theory[J]. Computational Material Science, 2012,53:340-346.

[24] 赵永辉. 气动弹性力学与控制[M]. 北京: 科学出版社, 2006.

Transfer function method for the flutter of aircraft wings with an external store

DUAN Jingbo1,2, JIANG Tao2

(1. College of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China；2. Department of UAVEngineering, Ordnance Engineering College, Hebei 050003, China)

The transfer function method was applied to analyse the flutter of aircraft wings carrying an external store. The flutter differential equation of a clean wing was established by combining the bending-twist vibration equation of the wing and the Therdorson’s unsteady aerodynamics model. The external store hung below the wing by a pitch spring was regarded as a rigid body owning a certain mass and rotary inertia. Then, the influence of the external store on the wing flutter was introduced by considering the conditions of deformation harmony and internal force balance. Further, using the transfer function method, the control equations ware formulated in a state-space form by defining a state vector. Both the flutter velocity and flutter frequency were obtained by solving a complex eigenvalue problem. The results are in good agreement with the literature solutions and the finite element solutions, which indicates that the present method is accurate and efficient. Finally, the effects of the mass, rotary inertia, position and pitch stiffness of the pylons ware investigated.

aircraft wing with an external store; unsteady aerodynamics; flutter; transfer function method

中国博士后科学基金(2014M560803)

2015-11-02 修改稿收到日期： 2016-01-04

段静波 男，博士后，讲师，1982年4月生

V215.3

A

10.13465/j.cnki.jvs.2017.10.018