同解视角下对单纯形法的理解

贺学海，张 彬

同解视角下对单纯形法的理解

贺学海，张 彬

(商丘职业技术学院，河南 商丘 476000)

对线性方程组的增广矩阵实施初等变换，变换后所对应方程组与原线性方程组同解．借助该理论，将线性规划问题标准型中的目标函数系数及约束条件中的增广矩阵按一定方法组成新的矩阵，通过基变量的换基迭代原理对新矩阵进行初等变换，符合一定要求后，通过变换后的矩阵求出线性规划问题的最优解．

同解；线性规划；单纯形；最优解

引言

线性规划基础模型是数学模型的重要类型，其在运筹学方面的应用非常广泛，单纯型法是美国数学家G.Dantzig1947年创建，它在解决线性规划模型时简捷、实用，是公认的行之有效的方法．文献[1]通过实例探讨了单纯形法步骤和应注意的问题，文献[2]就线性规划的单纯形法及其发展进行了探讨，文献[3]就线性规划问题的广义单纯形法进行了研究，文献[4]讨论了对偶单纯形法实质就是单纯形法,本质是在运用对偶单纯形法解决线性规划问题将单纯形表旋转90°进行．由于信息技术的发展，单纯型法在解决线性规划问题时可以应用标准软件通过计算机来求解，然而理论基础作为原理性的东西不能抛弃．本文根据单纯形法理论结构，巧妙的利用目标函数和约束条件决策变量的系数构造出一个矩阵，利用“换基迭代”原理对矩阵进行初等变换，通过对变换后的矩阵的观察，得出线性规划问题何时出现无解、有最优解、无穷多最优解．

1 单纯形法原理

1.1 基本思想

先找出一个基可行解,其方法是由约束方程组的系数矩阵找出子块为单位阵In×n,则可作为初始可行基，在没有的情况下可采用人工变量法寻找[7]．然后根据最优性原则确定是否为最优解,是则结束；不是则利用换基迭代寻找下一个基可行解，并且使下一个基可行解的目标函数有所改变，反复多次，直到找出最优解，或判断出原问题无最优解．

1.2 基本理论

用单纯形法求线性规划问题最优解时,常将问题化为标准型(非标准型可通过恒等变换和引入松驰变量等方法化为标准型):

其矩阵形式为

minf=CX

将A的列向量重排次序成A=(BN) ,相应X=(XBXN)T,C=(CBCN),XB为基变量,XN为非基变量(若约束方程组中没有现成的初始基,用人工变量法可得到初始基).于是

f=CBXB+CNXNAX=BXB+NXN=b

则:

XB=B-1b-B-1NXNf=CBB-1b+(CN-CBB-1N)XN

令非基变量XN=0,解得基变量XB=B-1b,称(XBXN)为基解,当XB的值都非负时,则称为基可行解.

若进一步满足:CN-CBB-1N≥0,则对一切可行解X,必有f≥CBB-1b,此时称基可行解X=(B-1b,0)T为最优解，当条件不满足时,可通过“换基迭代”使条件满足，从而得到线性规划问题最优解．

1.3 初等变换视角下的“换基迭代”

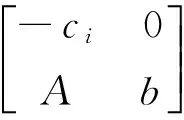
1.4 最优解的讨论

2 利用矩阵初等变换求线性规划最优解

单纯形法求线性规划问题最优解的过程,实际是在表格中实施的,称之为单纯形表.而每个单纯形表可用一个矩阵来代替,每次的换基迭代本质上是对矩阵的初等变换.

2.1 矩阵的构成

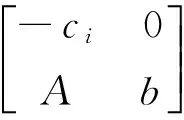
2.2 应用举例

此例来源于某工厂生产计划，求目标函数f的最小值．

minf=x1-3x2+2x3minf=x1-3x2+2x3

根据2.1构成矩阵并做初等变换

矩阵中满足-ci≤0(-11为f除外)，这说明非基变量从0增大为一个正数时，f必然增大，因此minf=-11，此时其最优解为(x1,x2,x3,x4,x5,x6)T=(4,5,0,0,0,11)T．

本文介绍的方法最大的优点是避开冗长的理论和论证，只要掌握矩阵的初等变换，就可以解决一般的线性规划问题．

[1]贺学海．单纯型法解决LP问题的研究 [J]．沈阳师范大学学报，2010,01，14-16.

[2]燕子宗 费浦生 万仲平．线性规划的单纯形法及其发展[J]．计算数学，2007，29(1)1-14.

[3]邹自德．线性规划问题的广义单纯形法 [J]． 电子科技大学学报，1997，26(增刊)， 143-148.

[4]林海明．线性规划对偶单纯形法的常识性经济解释[J]．数学的实践与认识，2003，33(10).

[5]阎章杭，周建国，黄士林．高等数学与应用数学基础[M]．北京：中国人民公安大学出版社，2001，127-144.

[6]罗雁，简金宝，吴志远．线性规划一种改进的对偶单纯形法[J]．桂林工学院学报，2005,25(2)，263-266.

[7]王全文，吴育华，吴振奎，等．单纯形法选择进出基变元的一个新准则[J]．数学的实践与认识，2009，39(14)．

The Interpretation of the Simplex Method from the Perspective of Same Solution

HE Xue-hai，ZHANG Bin

(Shangqiu Vocational and Technical College, Shangqiu Henan 476000, China)

After the elementary transformation of the augmented matrix of linear equations, the transformed equation system and the original linear equation system are equivalent. With the aid of the theory above, the new matrix could be formed based on the augmented matrix of objective function and constraint condition in standard form of linear programming. Then, after the elementary transformation on the new matrix by the way of basis iteration and meeting certain requirements, the optimal solution in linear programming could be obtained by the transformed matrix.

the same solution; linearity programming; simplex; optimal solution

1673-2103(2017)02-0005-03

2017-02-12

河南省教育厅教学改革资助项目(2014SJGX386)

贺学海(1962-)，男，河南社旗人，教授，硕士，研究方向：函数论及应用数学.

O221．1

A