淘尽黄沙始见金

林发辉

[摘 要] 行程问题的基本量为路程、速度、时间，三者的关系为：路程=速度×时间（s=vt），行程问题除了路程关系，还有关于时间的描述（时间关系）和速度关系. 解复杂的应用题时，设未知数，列方程都需要根据相等关系进行.

[关键词] 相遇问题；追及问题；相等关系；应用题；行程问题

内容综述

行程问题是应用题中较重要的题型之一，也是较难的题型之一，很多学生对应用题有畏难情绪，就是从学行程问题开始的. 究其原因，第一，行程问题涉及的变化较多，有的涉及一个物体的运动，有的涉及两个甚至多个物体的运动. 涉及两个物体运动的，又有“相向运动”（相遇问题）、“同向运动”（追及问题）和“相背运动”（相离问题）三种. 第二，行程问题需要学生敏锐发觉多个量之间的关系，如时间关系、速度关系、路程关系及时间、速度、路程之间的关系. 第三，行程问题需要学生熟练运用一些综合方法解决问题，如方程思想、函数思想、不等式等. 本文主要讨论行程问题之相遇问题和追及问题.

教学内容再现

例1 甲、乙两站相距1080千米，一列快车从甲站开出，每小时行驶72千米，一列慢车从乙站开出，每小时行驶48千米，两车相向而行，几小时后相遇？

分析 画路程图找路程关系，快车的路程+慢车的路程=总路程（如图1）.

解答 设两车相向而行，x小时后相遇，则有72x+48x=1080，解得x=9. 所以两车相向而行，9小时后相遇.

变式1 甲、乙两站相距1080千米，一列快车从甲站开出，每小时行驶72千米，一列慢车从乙站开出，每小时行驶48千米，两车相向而行，若快车先开1小时，则慢车开出多少小时后与快车相遇？

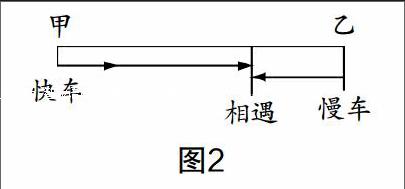
分析 画路程图找路程关系，快车的路程+慢车的路程=总路程（如图2）.

解答 设慢车开出x小时后与快车相遇，则有72（x+1）+48x=1080，解得x=8.4. 所以慢车开出8.4小时后与快车相遇.

变式2 甲、乙两站相距1080千米，一列快车从甲站开出，每小时行驶72千米，一列慢车从乙站开出，每小时行驶48千米，两车相向而行，若慢车先开2小时，则慢车开出多少小时后与快车相遇？

分析 画路程图找路程关系，快车的路程+慢车的路程=总路程（如图3）.

解答 设慢车开出x小时后与快车相遇，则72（x-2）+48x=1080，解得x=10.2. 所以慢车开出10.2小时后与快车相遇.

变式3 甲、乙两站相距1080千米，一列快车从甲站开出，每小时行驶72千米，一列慢车从乙站开出，每小时行驶48千米，两车相向而行，若两车同时开出，则开出多少小时两车相距120千米？

分析 （1）相遇前：画路程图找路程关系，快车的路程+慢车的路程+120=总路程（如图4）.

（2）相遇后：画路程图找路程关系，快车的路程+慢车的路程-120=总路程（如图5）.

解答 （1）设两车同时开出，开出x小时后两车还相距120千米才相遇，则有72x+48x+120=1080，解得x=8.

（2）设两车同时开出，开出x小时后两车背向相距120千米，则有72x+48x-120=1080，解得x=10.

综上所述，两车同时开出8小时或10小时，两车相距120千米.

例2 A，B两地相距480千米，一列慢车从A开出，每小时行驶50千米，一列快车从B开出，每小时行驶90千米.两车同时开出，若同向而行，快车在慢车后面，几小时后快车追上慢车？

分析 画路程图找路程关系：快车走的路程=慢车走的路程+480（如图6）.

解答 设两车同时开出，若同向而行，快车在慢车后面，x小时后快车追上慢车. 可得90x=50x+480，解得x=12. 所以两车同时开出，若同向而行，快车在慢车后面，12小时后快车追上慢车.

一点见解

利用行程图找路程关系，这种方法是极好的. 因为图形直观、形象，它体现了数形结合思想. 著名数学家华罗庚先生说：“数与形，本是相倚依，焉能分作两边飞？数缺形时少直观，形少数时难入微. 数形结合百般好，隔离分家万事休. 切莫忘，几何代数统一体，永远联系莫分离. ” 行程问题除了路程关系，还有关于时间的描述（时间关系）和速度关系. 教者似乎觉得时间和速度关系太简单了，因此忽略了对它们的分析. 然而，笔者认为它们一样重要. 关于时间的描述，描述的是运动物体的时间关系，这种关系常用在设未知数上.

关于时间的描述有：同时（即两运动物体的时间相等）、先出发（即先出发的物体时间多）、晚出发（即晚出发的物体时间少）、迟到或晚点（即遲到或晚点的物体时间多）、早到（即早到的物体时间少）、停留或耽搁（即停留或耽搁的物体时间少）等.

笔者试举一例说明此类教法.

例3 甲、乙两人相距40千米，甲先出发1.5小时后乙再出发，甲在后乙在前，二人同向而行，甲的速度是每小时8千米，乙每小时比甲少走2千米，甲出发几小时后追上乙？

分析 画行程图找路程关系（如图7）.

路程关系：由图及题意得甲走的路程比乙走的路程多40千米，即甲的路程=乙的路程+40.

时间关系：由“甲先出发1.5小时”可知甲多用了1.5小时，即甲的时间=乙的时间+1.5.

速度关系：由“甲的速度是每小时8千米，乙每小时比甲少走2千米”得甲的速度是每小时8千米，乙的速度是每小时6千米.

由时间关系间接设未知数（当然，直接设未知数也不难，只需把时间关系稍微变形）：设乙出发x小时被追上，则甲的总时间为（x+1.5）小时. 可得8（x+1.5）=6x+40，解得x=14. 14+1.5=15.5（小时）. 所以甲出发15.5小时后追上乙.

笔者以为，解复杂的应用题时，设未知数、列方程都需要根据相等关系进行. 不能在未进行分析的情况下“问什么就设什么为未知数”，应根据实际情况决定是否要间接设未知数.