浅谈初中数学教学中实验渗透的有效性

董香凤

[摘 要] 数学学习需要各种手段交替进行，需要严密的逻辑证明，需要感性的直观认识，需要操作的实验感知，需要巧妙的猜想归纳等. 在数学教学中渗透数学实验，对于培养学生的数学学习兴趣、提高学生的数学学习动手能力来说，都有益.

[关键词] 初中数学；数学实验；动手；直观；频率；统计

众所周知，数学教学有很多呈现方式，特别是对于刚刚进入初中学习的学生而言，多元化的学习方式恰恰是最需要的. 从小学到初中，学生思维特征转换尚未完全实现，学生可以接受一定的抽象数学，但又不能完全达到理解的地步. 大多数初中数学完成了从感性向不断理性证明的过程，因此各种平面几何的证明、二次函数的分析大大降低了学生数学学习的积极性. 笔者认为，需要在适当环节加入多元的学习手段，通过非形式化的手段、具象化的展示，将这种形式化的论证过程通过数学实验加以渗透，以提高教学的有效性.

深化知识

很多数学核心概念都是经过上百年甚至更久的时间形成的，它不可能在短时间内让学生迅速完全理解，并掌握它所有的内涵. 为了加快学生对这样的核心概念的理解，笔者认为可以设计一些具备概念外延、表象的情境，来加深学生对相关数学概念的理解，进而感受概念.

案例 复习“函数”概念及其相关问题，多元复习设计，加强概念理解，提高问题解决能力.

函数概念是中学数学最重要的概念，是最核心的数学概念. 初中数学对函数的表述是以变量和变量的关系进行总结的，这种关系对于学生来说感受并不到位. 笔者对函数概念进行了重新设计，从三个层面层层递进地推进对函数概念的认识，从而提高函数教学的有效性和深度.

设计1 （视频实验）用视频展示如何将大米加工成各种各样的食品，如面粉、糕点、面条、包子等.

设计意图 函数关系最根本的体现是变量与变量之间的关系，如何让学生首先从感性认识中体会这种变量与变量的关系呢？笔者设计的是利用数学视频实验将同样的大米不断地放入不同的加工机，产生各种不同的制成品. 学生容易理解这样的生活情境，同时又心存疑惑：为什么要放这样的视频呢？这与今天要学习的函数知识有关系吗？这一视频实验在向学生不断渗透一个知识信号：任何函数都是以x（数）为自变量，经过不同的对应法则（加工机）得到不同的新的y（因变量）的一种对应关系.

设计2 （图形实验）请学生在学案中绘制正确的函数图像若干幅（如图1、图2、图3）.

设计意图 通过函数图像“形”这一特点，利用学生在学案上绘制的函数图像，课堂中直接利用几何画板将学生绘制的、有效的、有价值的函数图像给以呈现. 笔者将这一设计称之为教学中的图形实验，其意图是通过函数图像中“形”这一显著特点，让学生充分理解函数概念阐述的变量与变量之间的直接对应关系，即每一个自变量x对应唯一的一个因变量y. 在这一图形实验设计环节，有不少学生提供了有创新意义的函数图形，比如图3，学生画了类似体育标记“耐克”的函数，这一图像让学生在学习函数的过程中体会到了其在生活中所具备的形态，让数学学习根植于生活、运用于生活.

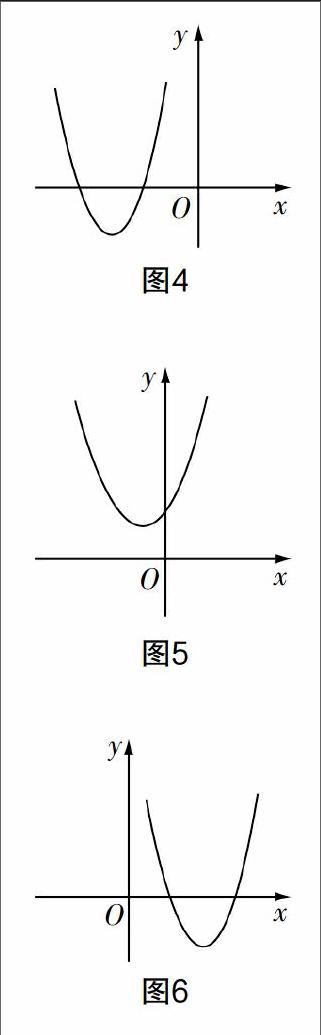
设计3 （动态试验）利用现代信息技术教育手段，从动态变化中研究函数问题. 如研究二次函数相关问题：函数y=x2-2mx+8在-1≤x≤1的最小值为1，求m的值.

设计意图 对于初中生而言，含有参量m的值让学生对于问题的思考变得不太直观，更因为自变量x受限于范围-1≤x≤1，所以初中生普遍不能接受问题的含义. 笔者设计了动态试验，利用几何画板中的参数功能，让函数随着参数m的变换而变化（图4、图5、图6），从中可以清晰地看出在参数变换的过程中，其最小值并不完全由对称轴处的值确定，这会与初中生脑海中“在顶点处取到最值”这一固有思维形成认知冲突. 可以请学生分析此函数问题为何要分类讨论，有没有与函数概念相悖，分类的依据是什么等，从而提高函数内容复习的深度和有效性.

不难发现，层层递进的相关实验操作，学生已经感受到了数学的可操作性，思考了知识的延续性、承接性，这对函数知识学习的深化起到了一定的复习效果. 从课程理念来说，这种一边实验一边研究的方式，能让学生体会到数学多元的学习途径，能让学生在严密逻辑推理的同时结合感性的实践操作加深对知识的理解，提升复习的有效性.

理解概念

部分数学概念需要通过实验去理解，比如八年级数学中随机事件概率的定义. 概率是统计中的重要概念，其来源可以通过大量的数学实验进行操作，即通过“频率与机会”一课来学习概率的概念.

1. 教学设计

（1）为了让学生充分理解随机事件频率值是一个随着实验次数而不同的、较稳定的值，所以课堂教学采取了大量的数学实验操作来加强学生的理解.

（2）通过讨论、思辨，使得学生理解频率的稳定值即为概率，每一次实验频率值都不相同，但概率不随实验次数的改变而改变.

（3）（课后）与学生一起重做蒲丰投针问题，感受概率是频率的稳定值这一重要特性.

2. 实验操作

（1）教师选择概率中的经典实验：抛硬币. 记抛出正面为上为事件A，将学生分成10个小组，每组中两位学生负责抛硬币，两位负责记录. 总次数分别为10次、20次、50次、100次、自定义次.

（2）请学生绘制表格，将抛出正面为上的次数分别记录下来，计算出抛出正面为上的次数占总次数的百分比.

（3）请学生观察：每组学生都有五组数据，有十个小组，共五十组数据. 数据分析从两方面入手：一，各自小组内部的数据分析及频率值变化；二，班级五十组数据的研究分析及频率值变化，从数据中感受频率值与实验次数的关系（如表1）.

（4）从多次实验，特别是大数据实验的结果来看，我们都发现正面向上的频率始终稳定在某一个常数左右，频率值随实验次数的不同而不同，但是实验次数越多，频率值越趋向于某一个常数，这种直观感受越明显.

设计意图 从概率的角度来说，概率论本身就是一门有关数学实验的章节，笔者以经典的抛硬币实验为载体设计了本课相关的数学教学. 这一实验所需设备简单，可操作性强，并且通过多次实验产生的数据可以产生新的思考，引发学生思考为什么实验次数越多，正面向上频率值越趋向于某一个常数. 从学生亲自动手操作的实验中，学生认识了频率概念的意义：频率并不是固定不变的常数，它与每一次实验有关，一般来说，每次实验所得到的频率值不相同，但随着实验次数的增加，频率值愈来愈稳定地趋向于某一个常数. 这样的数学实验能让学生深刻理解频率到底是一个什么样的数学概念，后续可以进一步向学生介绍概率值的意义，以及各种有趣的数学实验，如蒲丰投针问题等，让数学实验融入数学教学中，增强学生的数学学习兴趣，提高学生数学概念的理解能力.

总之，数学实验是数学教学有益的补充. 近年来，数学课程标准提出了让学生学习数学更多元的学习手段的要求，其中有关数学实验、数学探究性学习、信息技术在数学教学中的应用等，都是很好的尝试和方向. 筆者认为，加强多形式、多维度的教学方式的使用，对于学生数学学习兴趣的增加、主动性的增强都是有益的，更能从不同的角度加深对知识的理解，从而提高教学有效性.