一类具有离散时滞和分布时滞的BAM神经网络的全局耗散分析

谭 亮, 钟守铭

(电子科技大学 数学科学学院, 四川 成都 611731)

一类具有离散时滞和分布时滞的BAM神经网络的全局耗散分析

谭 亮, 钟守铭*

(电子科技大学 数学科学学院, 四川 成都 611731)

研究了带有离散时滞和分布时滞的BAM神经网络的全局耗散性问题;利用Lyapunov稳定性理论和线性矩阵不等式，通过构造Lyapunov泛函，得到了判定具有时变混合时滞的BAM神经网络系统是全局耗散的新准则;通过实例仿真，表明了所得结论的有效性.

双向联想记忆(BAM)神经网络； 时变时滞； 全局耗散； Lyapunov稳定性理论； 线性矩阵不等式

B. Kosko[1-2]将单层单向联想记忆网络推广到双层双向结构，提出了双向联想记忆(BAM)神经网络系统，迄今已将BAM神经网络系统应用于联想记忆、人工智能、最优化等方面，取得了许多成就[3-5].由于神经元之间交换信息及信号传输等实际过程都存在信息延迟，时滞将导致网络系统的性能发生改变，从而使稳定的系统变得不稳定，甚至使系统的演化变得更加复杂.但是，可以通过控制时滞来优化动力系统[5]，所以研究有时变时滞的BAM神经网络真实地模拟现实处理信息,具有深远的实际意义[3-4].

近年来，时变时滞神经网络耗散性的研究得到了越来越多的关注:文献[6-10]研究了具有时变时滞的BAM神经网络的指数稳定性和全局指数耗散性,文献[11]讨论了BAM神经网络系统平衡点的全局渐近稳定性问题,文献[12]通过线性矩阵不等式研究了BAM神经网络不确定时滞系统的鲁棒耗散性,文献[13]通过构造合适的Lyapunov函数研究了具有无约束时滞神经网络的全局耗散性,文献[9]利用M矩阵以及线性矩阵不等式的形式研究了常时滞的神经网络的耗散性.这些研究对神经网络全局耗散性能的分析非常重要，在工程中也有广泛的应用[14-18].本文通过构造Lyapunov泛函,建立判定BAM神经网络系统全局耗散的新准则，以及实例仿真验证了所得结论的有效性.

1 问题描述

考虑如下带有离散时滞和分布时滞BAM神经网络系统:

(1)

ui和vj分别表示i层和j层的神经元状态.

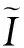
(2)

其中u1、u2、σ、τ均为正实数,i=1,2,…,n,j=1,2,…,m.

时滞核函数Kij,Pji:[0,∞)→[0,∞)分段连续，且满足

(3)

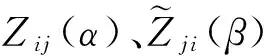
神经元激励函数hi、wj满足如下假设:

1)hi、wj在R上有界，i=1,2,…,n,j=1,2,…,m;

(4)

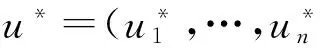
(5)

其中

由hi、wj满足假设的条件可推得激励函数gi、fj满足如下条件：

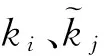
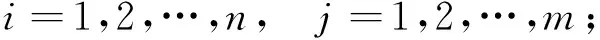
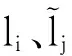
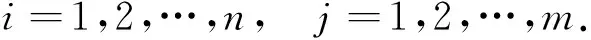
考虑系统(5)的初始条件为:

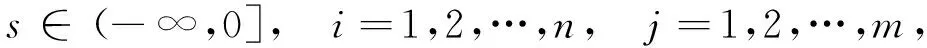
其中φi(s)、φj(s)在(-∞,0]上连续且有界.

定义 1[13]BAM神经网络系统(5)称为耗散系统，如果存在紧集Ω∈Rn+m，φi(s)、φj(s)是连续有界函数，使得系统(5)的解x(t,φ)、y(t,φ)满足：存在T>0,对∀t≥T有[xT(t,φ),yT(t,φ)]T∈Ω,则Ω是系统(5)的全局吸引子集.

定义 2[13]假设Ω是BAM神经网络系统(5)的全局吸引子集，那么系统(5)被称为全局指数耗散系统，如果存在紧集Ω1，满足Ω⊂Ω1⊂Rn+m，使得∀ξ∈Rn+mΩ1，存在M(ξ)>0,α>0，满足

则Ω1是全局指数吸引子集，其中

引理 1[19]如果a、b是n维实向量，P是一个n×n正定矩阵，则有

2aTb≤aTP-1a+bTPb.

(6)

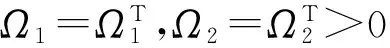
(7)

2 主要结果及证明

为了定理叙述方便，先定义一些必要的参数和相关的矩阵.令

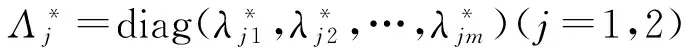
(8)

(9)

证明 定义Lyapunov泛函

(10)

其中

对Vi(t)(i=1,2,3)沿着系统(5)的轨迹求导得

运用引理1，存在正定的矩阵P满足

由于τ<1,σ<1,同理有

运用不等式对任意a,b∈R有2ab≤a2+b2，可得:

即得:

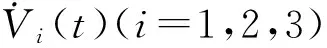
(14)

由引理2可得

定理 2 BAM神经网络系统(5)是全局指数耗散系统，Ω1是全局吸引子集，如果Ω1满足

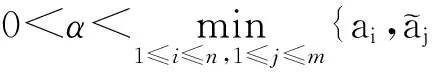
证明 取泛函

对V(t)沿着系统(5)的轨迹求导可得

其中(xT(t),yT(t))T∈Rn+mΩ1.对(15)式的两端积分可得

因此,Ω1是全局指数吸引子集，系统(5)是全局指数耗散系统.

3 实例仿真

考虑如下的模型:

1) 验证定理1，取相关的参数如下：

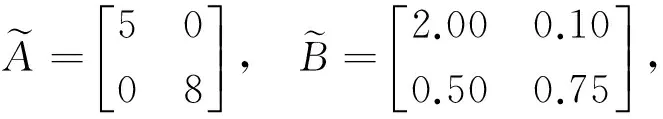
可以算得

令u1=0.16,u2=0.1,Λ1、Λ2为单位矩阵，经LMI验证：当σ值在0.1～0.9变化时，τ的最大值均可取到0.999 9；反之当τ的值在0.1～0.9变化时，σ的最大值均可取到0.999 9.所以本文的结论对时滞有较大的可行范围.

2) 为了方便验证定理2，依然取与定理1中相同的矩阵参数,且令:

根据定理2可知系统(5)是全局指数耗散系统，而且

因此Ω1是全局指数吸引子集，其中0<α<4.

[1] KOSKO B. Adaptive bi-directional associative memories[J]. Appl Opt,1987,26:4947-4960.

[2] KOSKO B. Bi-directional associative memory[J]. IEEE Trans Syst Man Cybern,1988,18:49-60.

[3] 韩力群. 人工神经网络理论、设计及应用[M]. 北京:化学工业出版社,2002:1-139.

[4] 蔡自兴,徐光佑. 人工智能及其应用[M]. 北京:清华大学出版社,2010:1-169.

[5] 曹金玲. 时滞神经网络模型的动力学研究[D]. 南京:东南大学,2006.

[6] CAO J D, DONG M F. Exponential stability of delayed bi-directional associative memory networks[J]. Appl Math Comput,2003,135:105-112.

[7] LI C D, LIAO X F, ZHANG R. Delay-dependent exponential stability analysis of bidirectional associative memory neural networks with time delays:an LMI approach[J]. Chaos, Solitons and Fractals,2005,24:1119-1134.

[8] LIANG J L, CAO J D. Exponential stability of continuous-time and discrete-time bidirectional associative memory neural networks[J]. Chaos, Solitons and Fractals,2004,22:773-785.

[9] LIAO X X, WANG J. Global dissipativity of continuous-time recurrent neural networks with time delay[J]. Phys Rev,2003,E68(1):1-7.

[10] LOU X Y, CUI B T. Absolute exponential stability analysis of delayed bi-directional associative memory neural networks[J]. Chaos, Solitons and Fractals,2007,31:695-701.

[11] ARIK S, TAVSANOGLU V. Global asymptotic stability analysis of bidirectional associative memory neural networks with constant time delays[J]. Neurocomputing,2005,68:161-176.

[12] SERON M M, HIL D J, FRADKOV A L. Nonlinear adaptive control of feedback passive systems[J]. Automatica,1995,31(7):1053-1060.

[13] SONG Q K, ZHAO Z J. Global dissipativity of neural networks with both variable and unbounded delays[J]. Chaos, Solitons and Fractals,2005,25:393-401.

[14] LIAO X X, LUO Q, ZENG Z G. Positive invariant and global exponential attractive sets of neural networks with time-varying delays[J]. Neurocomputing,2008,71:513-518.

[15] ZHANG Q, WEI X P, XU J. Global exponential convergence analysis of delayed neural networks with time-varying delays[J]. Phys Lett,2003,A318:37-44.

[16] ZHANG J Y. Globally exponential stability of neural networks with variable delays[J]. IEEE Trans Circ Syst I,2003,50(2):288-291.

[17] TU Z W, JIAN J G, WANG B X. Positive invariant and global exponential attractive sets of a class of neural networks with unbounded time-delays[J]. Commun Nonlinear Sci Numer Simul,2011,16:738-745.

[18] CAO J D, CHEN T P. Globally exponentially robust stability and periodicity of delayed neural networks[J]. Chaos, Solitons and Fractals,2004,22(4):957-963.

[19] XU S, LAM J, HO D W C, et al. Global robust exponential stability analysis for interval recurrent neural networks[J]. Phys Lett,2004,A325(2):124-133.

[20] BOYD B S, GHAOUI L E, FERON E, et al. Linear Matrix Inequalities in Systems and Control Theory[M]. Philadephia:SIAM,1994.

2010 MSC：34D20; 92B20

(编辑 周 俊)

Global Dissipativity of a Class of BAM Neural Networks with Discrete and Distribute Time Delays

TAN Liang, ZHONG Shouming

(SchoolofMathematicsScience,UniversityofElectronicScienceandTechnologyofChina,Chengdu611731,Sichuan)

In this paper, we investigate global dissipativity for BAM neural networks with discrete and distribute delays. The Lyapunov stability and the linear matrix inequality (LMI) approach are employed in our work. By establishing a new Lyapunov functional, we obtain novel criteria for global dissipativity analysis. Some numerical examples are given to illustrate the effectiveness of the proposed method.

bi-directional associative memory; time-varying delays; global dissipativity; Lyapunov stability method; linear matrix inequality

2015-10-26

国家自然科学基金(61273015)

O175.13

A

1001-8395(2017)01-0011-07

10.3969/j.issn.1001-8395.2017.01.002

*通信作者简介：钟守铭(1955—),男,教授,主要从事动力系统与控制论的研究,E-mail:zhongsm@uestc.edu.cn