航空瞬变电磁中MPI并行计算分析
陈 辉, 杜兴忠, 杨正刚, 江晓涛
(中国电建集团 贵阳勘测设计研究院有限公司,贵阳 550081)
航空瞬变电磁中MPI并行计算分析
陈 辉, 杜兴忠, 杨正刚, 江晓涛
(中国电建集团 贵阳勘测设计研究院有限公司,贵阳 550081)
由于航空瞬变电磁的数据量很大,外加瞬变电磁反演方法耗时较大地电磁更多,为了在后期资料处理时减少不必要的耗时,对正演计算中的频时转换的方法做了一定研究,采用基于拉普拉斯尺度变换性质的Gaver-Stehfest变换做频时转换,适当减少了编写程序代码的行数及程序计算的时间消耗。针对现在的计算机很多都是多核的特点,研究了航空瞬变电磁一维反演的MPI(Message Passing Interface)并行计算,大大地节约了运算时间, 分析了并行计算时不同的多核CPU和不同的进程数时的加速比及并行效率。
航空瞬变电磁; 频时转换; G-S变换; 并行; MPI
0 引言
航空瞬变电磁法(Airborne Transient Electromagnetic Method, ATEM)是依托飞机运载,发射脉冲电流,在发射机断开电流时,观测二次场随时间的变化特性,进而推测地层中不同物质的分布特点,从而解释各种地质问题的方法[1-2]。该方法能够克服复杂地形带来的难以施工的困难,具有低成本、勘探速度快、可大面积勘测、通用性好等优点,有利于探测较深目标体和相对低阻覆盖区的探测[1,3]。
很多学者对航空瞬变电磁一维、2.5维和三维正反演方面做了很多的研究,同时2.5维和3维航空瞬变电磁反演也达到较高的计算精度,但其计算效率太低,目前仍没有得到较好地解决,还在理论研究阶段。
在国内、外,并行处理技术的各种算法研究取得了一定的成果。Newman等[4]在电磁反演中成功运用并行算法,完成了多节点并行运算;陈金窗等[5]在微机网络上成功实现了 2.5 维 CSAMT 正演的并行计算;匡斌等[6]实现了三维有限差分深度偏移的并行算法; Siripunvaraporn等[7]完成了对三维大地电磁正演和灵敏度矩阵的并行计算;殷文[8]运用MPI并行技术对时频分布做了改进和应用研究,使运算效率大大提高;谭捍东等[9]通过频点并行的方式成功实现了大地电磁三维正演的并行计算,得到了很高的加速比,验证了并行算法的稳定性以及高效性;刘羽[10-12]基于PC机群实现了二维大地电磁Occam反演的并行计算研究;管健和[13]对电磁场有限单元法解释分布式做了并行计算研究;谢丽等[14]在基于MPI的分布式网络并行编程环境下,成功实现了瞬变电磁响应计算的并行算法研究;Siripunvaraporn等[15]研究了大地电磁反演中垂直磁场传递函数反演和并行实现;李焱和胡祥云[16-19]分析了大地电磁的MPI并行计算;张帆[20]利用基于GPU并行计算和基于MPI的并行计算相结合的计算模式对直流电法和大地电磁法已有的三维正演串行算法进行了并行化处理;张清等[21]实现了基于GPU的叠前时间偏移走时计算的并行算法;李小康[22]研究了频率域航空电磁法有限单元二维正演的并行计算;柳建新[23]探究了基于MPI瞬变电磁测深一维反演的并行算法;史维等[24]对长时窗长偏移距瞬变电磁测深正反演方法做了并行研究,减少了瞬变电磁法正反演的计算时间;刘鹏茂[25]研究了基于MPI的大地电磁二维正则化反演并行算法;许洋[26]研究了基于MPI的半航空电磁反演的并行算法。
1 ATEM正演计算
对于航空瞬变电磁正演计算,其装置一般是中心回线装置,航空瞬变电磁响应计算公式为式(1)[27]。
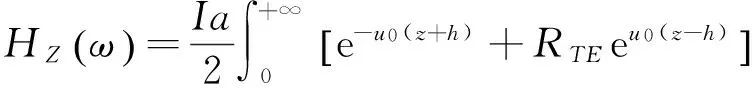

(1)
式中:J1代表一阶第一类贝塞尔函数;a为发射线圈的半径长度(m);λ表示积分的变量;RTE代表反射系数:
(2)
并且
(3)
(4)


(5)
式中:ω表示角频率;kn表示第n层的波数;σn表示第n层的电导率;一般情况下,通常取大地的导磁率μn等于自由空间的导磁率μ0;在准静态情况下取μ0=λ。
联立以上所有方程式可以完成航空瞬变电磁法一维正演模拟,其计算流程如图1所示。

图1 航空瞬变电磁一维正演流程图Fig.1 ATEM flow chart of one dimensional forward
由图1可以看出,在上述计算步骤中,涉及到了汉克尔变换和频时转换。汉克尔变换数值滤波计算方法比较成熟,经过长时间的推敲,拟采用Guptasarma等[28]研究的数字滤波方法。
查阅文献[28~30]可知,汉克尔积分变换的一般形式为:

(6)
式中:K(λ)为待变换函数;Ji为i阶第一类贝塞尔函数;r为一个已给定的值;K(λ)为被积函数。根据Guptasarma和Singh的研究得到汉克尔变换的计算公式为式(7):
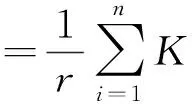
(7)
其中:λi=(1/r)×10[a+(i-1)s];i=1、2、…、n;Wi为滤波系数。
我们利用Guptasarma和Singh研究给出的汉克尔变换滤波系数,即一阶有47或120个系数,零阶有61或120个系数。
2 频时转换
2.1 G-S变换


(8)
式中:n是决定于计算机位数的正偶整数;Km是G-S变换系数,由式(9)算出。
Km= (-1)m+n/2·
(9)
式中:m=1、2、…、n,求和下限i1是(m+1)/2的整数部分。
[30],我们取n=12,根据式(9)求得的G-S变换系数如表1所示。
根据航空瞬变电磁中心回线装置,假设一个5层地电模型HKH,其模型参数设定为:电阻率从上到下分别为:100 Ω·m、10 Ω·m、50 Ω·m、5 Ω·m、100 Ω·m;层厚从上到下分别为:200 m、100 m、50 m、500 m、 ∞ m;发射线圈的半径为8 m;发射线圈中供电电流强度为1 A;发射线圈高度为50 m;

表1 G-S变换系数
根据航空瞬变电磁中心回线装置电磁响应计算式(1)和图1的一维正演计算流程,得到模型HKH的正演瞬变阶跃响应如图2所示。
2.2 基于Laplace尺度变换性质的G-S变换
在地球物理瞬变电磁法时频转换中,我们输入的时间序列通常是按某个公比输入,传统的G-S变换要求已知这一串时间数值,并用读文件的形式读入程序参与计算,这样对于写代码和程序计算时会产生额外的时间消耗。这里我们基于拉氏尺度变换性质提出一种改进的G-S变换,它只需要输入初始时刻及时间序列的公比,即可直接在程序中算出所需的N个时刻的值,这样减少了程序代码的行数及读文件的时间消耗,具有一定的实用价值。其具体做法是:
根据拉氏变换的尺度变换性质[31]:

那么可以将G-S变换式(8)改写为:

(10)
式(10)即为基于拉氏变换尺度变换性质的G-S变换。

图2 HKH地电模型一维正演电磁响应Fig.2 The airborne electromagnetic forward response of HKH model
分别用传统的G-S变换和基于拉氏尺度变换性质的G-S变换做频时转换计算前面模型HKH,得到的瞬变阶跃响应如图3(a),它们的相对误差见图3(b)。

图3 两种G-S变换得到的阶跃响应及它们的相对误差Fig.3 The step response value of two Gaver-Stehfest transforms and their relative errors(a)阶跃响应;(b)相对误差
由图3中可以看出,基于拉氏尺度变换性质的G-S变换得到的结果和传统G-S变换的结果虽然存在一定的差异,但差异非常小,相对误差最大为0.268%,最小为0%,完全能够满足电磁响应精度要求,说明这种基于拉氏尺度变换性质的G-S变换是正确可行的。
3 ATEM反演并行研究
3.1ATEM反演
在本次航空瞬变电磁一维反演的程序计算中,采用的是阻尼最小二乘法进行反演解释,它是马奎特[33](Marquardt)通过改进高斯-牛顿法的法方程组而得到的一种新的反演方法。对于目标函数为
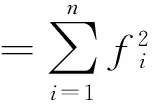
(11)
的极小问题,阻尼最小二乘法的做法是:
(JTJ+λI)δ=ε
(12)
其中:J表示雅可比矩阵;λ表示阻尼因子(它是一个正数,用以控制校正的方向和步长);δ是修正量即δ=pk+1-pk,从式(12)中可以明显看出它是λ的函数即δ=δ(λ),ε是残差向量。所以阻尼最小二乘法的迭代公式为式(13)。
pk+1=pk+(JTJ+λI)-1ε
(13)
在用阻尼最小二乘法反演解释时,主要阻尼因子的选取,当阻尼因子λ=0时,阻尼最小二乘法就变为了高斯-牛顿法;当阻尼因子λ=∞时,阻尼最小二乘法就变为了最速下降法,所以阻尼最想二乘法修正向量的方向是在高斯-牛顿法和最速下降法的修正方向之间,是介于高斯-牛顿法和最速下降法之间的某种插值,而阻尼因子就是这种插值的权系数。
Fletcher[34]提出根据函数φ(p)在迭代过程中实际的减小量比上,用理想二次型函数表示φ(p)的变化量,即:
(14)

判别阻尼因子 的增大或减小的标准一般是通过设定r值的上限和下限来实现的,可以这样设定:
1)当rk<0.25,增大阻尼因子λ。
2)当0.25 3)当rk<0.75,减小阻尼因子λ。 当需要增大阻尼因子λk时,可以令λ(k+1)=βλk,当需要减小阻尼因子λk时,可以令λk+1=λk/β。其中的β是一个大于“1”的正数,一般取为2~10之间的正数,它可以用式(15)计算出来。 (15) 在地球物理学反演算法中,雅克比矩阵J的计算精度与反演结果的准确性有直接关系,同样的对于雅克比矩阵的计算速度和计算精度问题,一直都是反演问题中的重点和难点。设从模型空间映射到数据空间的函数为φ,模型参数用p表示,则雅克比矩阵J可以表示为: (16) 式中:m表示观测数据的个数有m个;n表示模型参数的个数有n个。 在航空瞬变电磁法反演程序实现中,这里对雅克比矩阵行列中的每个元素的一阶偏导数的计算,采用有限差分方法中的一阶向前差分,即有: (17) 综上所述,用程序来实现阻尼最小二乘反演的具体流程见图4。 图4 阻尼最小二乘法反演解释流程图Fig.4 The flow chart of damping least squares inversion interpretation 根据反演计算流程,分别考虑对三层地电模型H和四层地电模型KH的一维反演解释。对于 型地电模型,模型从上到下的电阻率分别为100Ω·m、5Ω·m和200Ω·m,各层之间的厚度均为70m,飞行高度为50m。利用H模型正演得到的响应数据参与阻尼最小二乘反演,得到的反演结果如图5所示。对于KH型地电模型,模型从上到下的电阻率分别为10Ω·m、100Ω·m、10Ω·m和100Ω·m,各层之间的厚度均为50m,飞行高度为50m。利用 模型正演得到的响应数据参与阻尼最小二乘反演,得到的反演结果如图6所示。 图5 H型地电模型反演结果Fig.5 The inversion results of model H 图6 KH型地电模型反演结果Fig.6 The inversion results of model KH 由图5、图6可以看出,整个反演的效果是非常明显的,但是在对于地层中存在高阻情况时,反演得到的结果并不是很理想,对高阻体的反演解释不明显。造成这样的情况应该是多方面的综合影响结果,但最主要的可能有以下两个方面的原因:①在航空瞬变电磁法勘探中,对于地下的低阻情况是比较敏感的,而对于地下存在的高阻情况却不敏感,当地下存在高阻体时,由于航空瞬变电磁对其不敏感的特点,理论上的感应电动势响应就不明显,而其经过反演后所得的反演结果模型就会和理论模型之间存在较大的差异;②在反演解释方法的选择上,本次实验选择的反演解释方法是阻尼最小二乘反演法,其实也可以选择其他的反演方法,因为各种反演解释方法有不同的特点,所以应该根据实际情况来选择合适的反演方法,当然有时候为了取得更好的反演效果,还可以将多种反演方法配合使用。 3.2MPI简述及其性能评价 MPI(MessagePassingInterface)是消息传递方式并行程序设计的标准之一,它是一个函数库规范,并不是一门并行语言,它的操作就像是库函数的调用。我们完成用FORTRAN+MPI的并行语言编程,实现了航空瞬变电磁一维反演的并行计算研究。 对一个并行程序来说,效率评估的衡量参数有加速比与效率这俩最常用到的参数。先假设并行程序的每个进程独享处理器资源,在这样的前提下,设某个串行程序在某台并行机单处理器上的执行的时间为ts,对该程序并行化后,p个进程在p个处理器并行执行所消耗的时间为tp,那么该并行程序在该并行机上的加速比sp可定义为[32]: (18) 并行效率定义为式(19)。 (19) 3.3 MPI并行计算分析 由于反演中每次迭代都要计算雅克比矩阵J,都要重新修正初始模型,还要做正演计算,所以反演部分的耗时是最多的。因此,在设计其MPI并行程序主要还是对反演部分的雅可比矩阵计算做并行计算。采用主从模式,其并行计算的具体实现过程见图7。 图7 ATEM并行计算流程图Fig.7 The flow chart of ATEM parallel computing 本次并行计算设计的算例为前面的四层地电模型 模型。分别考虑了在双核单机下模拟多进程进行MPI并行的情况和不同处理器或者说不同线程相同进程进行MPI并行的情况,在这两种情况下分别比较了它们的加速比和并行效率,并进行了一定的分析。 对于双核单机下模拟多进程的情况,个人计算机的操作系统是Windows系统,配置是Pentium(R) Dual-Core CPU T4300 @ 2.10GHz处理器,内存是3.00GB。反演的并行计算结束所需要的时间、加速比和并行效率表2所示。 并行计算得到的反演结果并没有什么改变,如图8所示。 表2 KH模型反演并行计算不同进程运行结果 图8 并行计算得到反演结果模型Fig.8 Inverse model of parallel computing 从表2和图8可以看出,基于MPI的并行计算加快了运行的速度,使得耗费的时间变短,并没有改变反演的计算结果,说明这种并行是正确可行的。从表2中还可以看出,对同一种计算机或者说同一种处理器而言,此时增加并行的进程数,所耗费的时间就越短,加速比就越大,但是并行效率却在减小。这是因为对于p个进程而言,在理想的情况下,可以得到的最大加速比为p即线性加速,得到的效率为100%,但是此时并没有考虑到并行计算中的各种开销。事实上,随着进程数量的增加,由各种开销引起的耗时也会越多,计算通信比将大幅度减小,因而造成效率随着进程数增大而减小的现象。 对于不同的核心CPU而言,这里讨论三种核心CPU情况,分别为Pentium(R) Dual-Core CPU T4300 @ 2.10GHz、Intel(R) CoreTMi5 CPU M480 @ 2.67GHz和Intel(R) CoreTMi7-2860QM CPU @ 2.50GHz,它们分别是双核2线程、双核4线程和4核8线程。分别用它们做并行计算,这里只考虑1进程和8进程的反演部分并行计算情况,得到的反演计算结果如表3所示。 表3 KH模型反演并行计算不同线程运行结果 从表3中可以看出,对于不同核心CPU的时候,处理器的线程数越大所消耗的时间相对越少,加速比相对越大,并行效率也相对越高,同样它们经过并行计算得到的反演结果并没有被改变。 1)通过对正演计算中的频时转换研究,得到基于拉普拉斯尺度变换性质的G-S变换是正确可行的,它在保证满足航空瞬变电磁响应精度的前提下,减少了编写程序代码的行数及程序的计算时间消耗,具有一定的实用价值。 2)阻尼最小二乘法反演得到的反演解释结果可以看出,对于三层和四层地电模型而言,总体反演效果比较明显,但是在对于地层中存在高阻情况时,反演得到的结果并不是很理想,对高阻体的反演解释不明显。 3)对航空瞬变电磁法的反演部分做基于MPI的并行计算,和传统反演计算相比,并行计算加快了程序运算的速度,减少了计算的耗费时间,并不会改变正演和反演计算的结果。不同的处理器并行计算的耗费时间不一样,处理器的核心线程数越大,相对的耗时会越少,加速比相对越大,并行效率也相对越高。相同处理器不同进程数时,进程数量越多,相对耗费的总体时间越少,加速比相对越大,但是并行效率却在相对变低。 参考文献: [1] NABIGHIAN M N. Electromagnetic methods in applied geophysics: volume 2, application, parts A and B [M]. Society of Exploration Geophysics, 1991. [2] 王卫平. 频率域航空电磁法特点及应用[C].中国地球物理学会第二十六届年会、中国地震学会第十三次学术大会, 2010: 635-636. WANG W P. Frequency domain characteristics and its application of airborne electromagnetic method[C]. The Chinese geophysical society the 26th annual meeting and China earthquake to the 13th academic conference, 2010: 635-636.(In Chinese) [3] MACNAE J C, NABIGHIAN M. Electrical and EM methods, 1980-2005 [J]. The Leading Edge, 2005, 24(s1): 42-45. [4] NEWMAN G A, ALUMBAUGH D L. Three-dimensional massively parallel electromagnetic inversion[J].Geophysics, 1997, 128: 345-354. [5] 陈金窗,戴光明.微机网络并行计算及2.5维CSAMT正演的并行实现[J].物探化探计算技术,1997,19(2):103-107. CHEN J C,DAI G M.Micro-computer networked computing and 2.5-d CSAMT forward parallel computing[J].Computing Techniques for Geophysical and Geochemical Exploration, 1997,19(2):103-107.(In Chinese) [6] 匡斌, 李心友, 王真理, 等. 三维有限差分深度偏移的并行算法和实现[C]. 寸丹集-庆贺刘光鼎院士工作50周年学术论文集, 1998,12: 289-303. KUANG B, LI X Y, WANG Z L, et al. The design and implementation of parallel algorithm of 3-D Finite-Difference depth migration[C]. Cun Dan set - celebrate Liu Guangding academician work the 50th anniversary of the academic papers, 1998, 12: 289-303. (In Chinese) [7] SIRIPUNVARAPORN W, UYESHIMA M,EGBERT G.Three-demensional inversion for Network-Magnetotelluric data[J].Earth Planets Space,2004,56:893-902. [8] 殷文, 印兴耀. 基于MPI 的时频分布的改进及应用[J]. 地球物理学进展, 2005, 20(1): 165-169. YIN W, YIN X Y. The amelioration and application of time frequency distributions on the basis of MPI[J]. Progress in Geophysics, 2005, 20(1):165-169. (In Chinese) [9] TAN H D,TONG T,LIN C H.The parallel 3D magnetotelluric forward modeling algorithm[J]. Applied Geophysics,2006,3(4):197-202. [10]刘羽. 大地电磁Occam反演中拉格朗日乘子搜索的并行计算[J]. 物探化探计算技术, 2005, 28(4): 342-345. LIU Y. The parallel computation of l l SEARCHING in magnetotelluric occam inversion[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2005, 28(4): 342-345. (In Chinese) [11]刘羽, 王家映, 孟永良. 基于PC机群的大地电磁Occam反演并行计算研究[J]. 石油物探, 2006, 45(3): 311-315. LIU Y, WANG J Y, MENG Y L. PC cluster based magnetotelluric 2-D Occam's inversion parallel calculation[J]. GPP, 2006, 45(3): 311-315. (In Chinese) [12]刘羽. MT Occam并行反演方案及性能分析[J]. 武汉理工大学学报, 2007, 29(2): 136-140. LIU Y. Parallel MT Occam inversion scheme and its performance analysis[J]. Journal of Wuhan university of technology, 2007, 29(2): 136-140. (In Chinese) [13]管建和. 电磁场有限元法解释分布式并行计算的研究[D]. 北京: 中国地质大学, 2006. GUAN J H. Study of distributing and parallel computation of electromagnetic field finite method explaining[D]. Beijing:China University of Geosciences, 2006. (In Chinese) [14]谢丽, 胡文宝, 陆辉. 瞬变电磁响应计算的并行算法研究[J]. 长江大学学报(自然科学报), 2009, 6(4): 22-24. XIE L, HU W B, LU H. A study of parallel algorithm on the calculation of transient electromagnetic response[J]. Journal of Yangtze University (Nat Sci Edit) , 2009, 6(4): 22-24. (In Chinese) [15]SIRIPUNVARAPORN W, EGBERT G. WSINV 3D MT:Vertical magnetic field transfer function inversion and parallel implementation[J]. Physics of the Earth and Planetary Interiors, 2009, 173: 317-329. [16]李焱, 胡祥云, 杨文采,等. 大地电磁三维交错网格有限差分数值模拟的并行计算研究[J]. 地球物理学报, 2012, 55(12): 4036-4043. LI Y, HU X Y, YANG W C, et al. A study on parallel computation for 3D magnetotelluric modeling using the staggered-grid finite difference method[J]. Chinese Journal of Geophysics, 2012, 55(12): 4036-4043. (In Chinese) [17]李焱, 胡祥云, 金刚燮,等. 基于MPI的一维大地电磁并行计算研究[J]. 地球物理学进展, 2010, 25(5): 1612-1616. LI Y, HU X Y, KIMKANGSOP. Research of 1-D magnetotelluric parallel computation based on MPI[J]. Progress in Geophysics, 2010, 25(5): 1612-1616. (In Chinese) [18]李焱, 胡祥云, 吴桂桔,等. 基于MPI的二维大地电磁正演的并行计算[J]. 地震地质, 2010, 32(3): 392-401. LI Y, HU X Y, WU G J,et al. Parallel computation of 2-d magnetotelluric forward modeling based on mpi[J]. Seismology and Geology, 2010, 32(3): 392-401.(In Chinese) [19]胡祥云, 李焱, 杨文采,等. 大地电磁三维数据空间反演并行算法研究[J]. 地球物理学报, 2012, 55(12): 3969-3978. HU X Y, LI Y, YANG W C,et al. Three-dimensional magnetotelluic parallel inversion algorithm using data space method[J]. Chinese Journal of Geophysics, 2012, 55(12): 3969-3978. (In Chinese) [20]张帆. 基于MPI和GPU直流电法和大地电磁法三维正演的并行算法研究[D]. 北京: 中国地质大学, 2011. ZHANG F. Research on parallel algorithm for three dimentional forward modeling of DC resistivity method and magnetotelluric method based on MPI and GPU[D]. Beijing:China University of Geoscience , 2011. (In Chinese) [21]张清, 迟旭光, 谢海波,等. 基于GPU实现叠前时间偏移走时计算的并行算法[J]. 计算机系统应用, 2011, 20(8): 42-46. ZHANG Q, CHI X G, XIE H B.,et al.Parallel algorithm based on the travel time computing of pre-stack time migration using GPU[J]. Computer Systems & Applications, 2011, 20(8):42-46. (In Chinese) [22]李小康. 基于MPI的频率域航空电磁法有限元二维正演并行计算研究[D]. 北京: 中国地质大学, 2011. LI X B. A MPI based parallel calculation investigation on two dimensional finite element modelling of AEM[D]. Beijing: China University of Geosciences, 2011. (In Chinese) [23]柳建新, 刘鹏茂, 刘颖,等. 基于MPI瞬变电磁测深一维反演并行算法探究[J]. 物探化探计算技术, 2011, 33(5): 491-495. LIU J X, LIU P M, LIU Y,et al. Research of parallel computing technology about the direct one-dimensional inversion of transient electromagnetic on MPI[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2011, 33(5): 491-495. (In Chinese) [24]史维, 严良俊, 谢兴兵. MPI环境的并行算法在瞬变电磁正反演中的研究[J]. 工程地球物理学报, 2012, 9(1): 75-80. SHI W, YAN L J, XIE X B. Parallel algorithm of MPI in TEM forward and inversion[J]. Chinese Journal of Engineering Geophysics, 2012, 9(1): 75-80. (In Chinese) [25]刘鹏茂. 基于MPI大地电磁二维正则化反演并行算法研究[D]. 长沙: 中南大学, 2012. LIU P M. Parallel regularization inversion of 2-D MT data based on MPI[D]. Changsha: Central South University, 2012. (In Chinese) [26]许洋. 半航空电磁一维正反演研究[D]. 成都: 成都理工大学, 2014. XU Y. Study about 1D forward and inversion of SAEM[D]. Chengdu: Chengdu University of Technology, 2014. (In Chinese) [27]NABIGHIAN M N. Electromagnetic methods in applied geophysics: volume 1, theory [M]. Society of Exploration Geophysics,1988. [28]GUPTASARMA D, SINGH B. New digital linear filter for Hankel J0 and J1 transforms [J]. GEOPHYSICAL PROSPECTING, 1997, 45(5): 745-762. [29]KNIGHT J H and RAICHE A P. Transient electromagnetic calculations using the Gaver-Stehfest inverse Laplace transform method [J]. GEOPHYSICS, 1982, 47(1): 47-50. [30]罗延钟, 昌彦君. G-S变换的快速算法[J]. 地球物理学报, 2000, 43(5): 684-690. LUO Y ZH, CHANG Y J. A rapid algorithm for G-S transform[J]. Chinese Journal of Geophysics, 2000, 43 (5): 684-690. (In Chinese) [31]郑君里, 应启珩, 杨为理. 信号与系统(上册)[M]. 北京:高等教育出版社, 2000. ZHENG L J, YING Q H, YANG W L. Signals and systems[M]. Beijing:CHEP, 2000. (In Chinese) [32]张林波, 迟学斌, 莫则尧,等. 并行计算导论[M]. 北京: 清华大学出版社, 2006. ZHANG L B, CHI X B, MO Z Y. Introduction to parallel computing[M]. Beijing:Tsinghua University Press, 2006. (In Chinese) [33]陈乐寿,刘任,王天生. 大地电磁测深资料处理与解释[M]. 北京: 石油工业出版社, 1988. Chen L S, Liu R, Wang T S. The processing and interpretation of magnetotelluric sounding data [M]. Beijing: Petroleum Industry Press, 1988.(In Chinese) [34]FLETCHER R.A Modified Marquardt Subroutine for Nonlinear Least Squares [M].Harwell:Rpt.AERE,1971. 第39卷 第2期2017年3月物探化探计算技术COMPUTING TECHNIQUES FOR GEOPHYSICAL AND GEOCHEMICAL EXPLORATIONVol.39 No.2Mar. 2017 MPI parallel computing in airborne transient electromagnetic method CHEN Hui, DU Xingzhong, YANG Zhenggang, JIANG Xiaotao (Guiyang Hydropower investigation design and Research Institute, CHECC, Guiyang 550081, China) Becasue airborne transient electromagnetic data volume is huge and transient electromagnetic inversion method is more compared with the magnetotelluric time-consuming. It is necessary to apply parallel computing of the research on airborne transient electromagnetic to reduce the unnecessary time in data processing. With the advantages of most computers with multi-cores, parallel computing research can be easily used in airborne transient electromagnetic. We first analyzed the frequency-time conversion method in the forward calculation,using Gaver-Stehfest transform based on Laplace scale transform nature do frequency-time conversion. This appropriates to reduce the number of rows to write program code and program calculation of time consumption. And then studied airborne transient electromagnetic one dimensional inversion of MPI (Message Passing Interface) with parallel omputing, which greatly saves the operation time. The parallel computing is then analyzed with multicore cpus, different processes considering the speedup ratio and parallel efficiency. airbone transient electromagnetic; frequency-time conversion; gaver-stehfest transform; parallel computing; message passing interface 2016-05-09 改回日期:2016-07-25 贵州省科学技术基金([2013]2297) 陈辉(1988-),男,硕士,工程师,主要从事工程物探技术研究和应用, E-mail:281636258@qq.com。 1001-1749(2017)02-0161-09 P 631.2 A 10.3969/j.issn.1001-1749.2017.02.02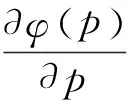







4 结论

