二维位场延拓的无网格方法研究

孔 倩, 李 鹏, 李 晶

( 1.华北电力大学 数理学院,涿州 071003 2.中国石油 东方地球物理公司,保定 072751 )

二维位场延拓的无网格方法研究

孔 倩1, 李 鹏1, 李 晶2

( 1.华北电力大学 数理学院,涿州 071003 2.中国石油 东方地球物理公司,保定 072751 )

位场向上延拓可归纳为求解函数所满足的Laplace方程，将无网格Galerkin(EFG)方法推广到二维位场延拓的数值计算中，详细论述了EFG方法的基本原理和具体实施过程，建立了无网格Galerkin法求解的离散方程，并进行了数值求解。同时与有限差分(FD)法的数值结果进行了比较，两种方法的求解结果基本吻合。介绍了EFG方法的应用实例，理论模型和实例的数值结果表明，EFG方法在处理二维位场延拓问题时是有效的且具有实现简单的特点。

位场延拓; 无网格Galerkin方法; 有限差分法; 正演计算

0 引言

在地球物理中，位场延拓是许多位场数据处理和正演计算中非常重要的步骤。二维位场的向上延拓通常会求解椭圆型的偏微分方程，已有的数值延拓方法包括有限差分法、有限元法、边界元法、积分方程法[1-9]。邓正栋等[1]采用有限差分法对三维稳定地电场进行了正演模拟，计算得出了地电异常体引起的异常电位场；尤淼等[2]针对二维位场延拓问题，探讨了有限差分方程的建模和计算过程，有限差分法求解过程简明而直观，但求解速度受网格剖分大小的影响，且数值稳定性和收敛性得不到保证[4]；郭荣文[5]从位场理论和有限元方法角度探讨了磁场向上延拓与模拟的有限元算法问题。有限元法可以处理复杂的几何形状，划分网格时更具有灵活性和适应性，比较容易地计算弯曲的物性界面和起伏地形，但输入输出的数据较多，对计算机的要求很高，且不适于处理无界区域[4]。电法勘探的边界元方法以徐世浙[7-9]的研究成果在国际上得到很高的评价，采用边界单元法对起伏地形二维位场向上延拓进行了数值模拟[7]，并模拟了二维地形对大地电磁场的影响[8]。边界元法只在研究区域的边界上剖分网格，计算量减少，但是对于边界元算法得到的大型矩阵方程往往是满秩的病态方程组[4]。因此针对位场延拓遇到的偏微分方程应研究有效的求解方法，有着非常重要的意义。

无网格方法是近年来迅速兴起的一种数值方法, 该方法不需要生成网格，而是按照一些任意分布的坐标点构造插值函数离散控制方程，可方便地模拟各种复杂形状的流场。研究表明[10-13]，无网格Galerkin (Element Free Galerkin，EFG) 方法具有收敛速度快，精度较高,计算稳定等优点，是无网格方法中较成熟的一种方法。因此，我们将EFG方法推广到二维位场延拓的数值计算中，讨论EFG方法模拟位场延拓问题的可行性。

1 基础介绍

建立一个三维的笛卡儿坐标系，将坐标系的xoy平面定为观测平面， 而其z轴向上为正。假定T(x,y,0)代表观测平面上的实际观测位场。于是，位场的向上延拓就是从已知的位场T(x,y,0)，推导出任意高度z(z>0)的位场T(x,y,z)，这就是根据位场的拉普拉斯方程式来确定著名的Dirichlet问题的解：

▽2T(x,y,z)=0

(1)

式中的变量z是观测平面上的延拓距离。

(2)

对式(2)拟采用无网格方法进行数值模拟，边界采用罚函数法处理。

2 EFG方法的基本原理[11-12]

EFG方法采用Galerkin变分原理对控制方程进行空间离散，对未知函数使用移动最小二乘法进行近似。由移动最小二乘法，待求函数u(x)在点x的邻域内可近似为式(3)。

(3)

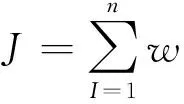
(4)

式中：w(x-xI)为节点的权函数；n为节点数目。

使式(4)中的J在驻点x达到最小，则可得到待定系数ai(x)满足如下方程组

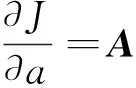
(5)

所以a(x)=A-1(x)B(x)u

式中：A=pTW(x)p，B=pTW(x)，u=(u1,u2,……,un)T， 将a(x)代入式(2)，则

(6)

3 模型求解

对式(2)采用上述EFG方法，取φi、φj为形函数ΦI(x)，边界条件采用罚函数方法[10]处理，α为罚因子，得到相应的变分形式为式(7)。

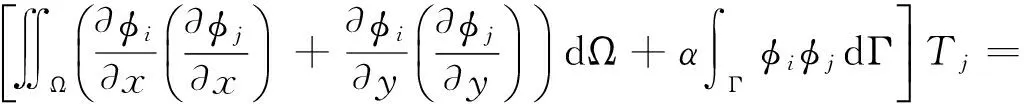
(7)

将式(7)，表述成下列矩阵形式：

KT=q

(8)

其中：

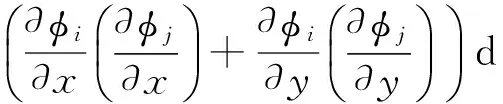
(9)

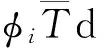
(10)

4 方法应用

4.1 理论模型1

有一水平地面测线，包含15个测点的场值信息。其中，地面边界上2号点～14号点磁场100nT，其余两点磁场为0nT(图1)。

图1 模型1中测点的场值信息
Fig.1 Field value in model 1

将模型1中x方向水平地面长度定为300 m，高度定为600 m。将上述问题归结为如下Laplace方程的求解：

(11)

用分离变量法求出的上述边界条件下的解析解：

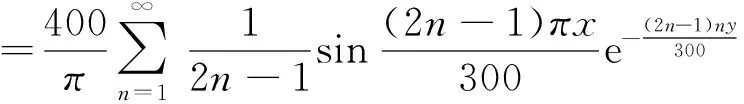
(12)

同时，分别采用EFG方法和有限差分(FiniteDifference,FD)方法求解上述方程。EFG方 法求解空间等间距均匀布置15×29个节点，四个本质边界条件节点上的罚因子取为1015。图2给出了模型1中采用EFG方法得出的整个求解区域的磁场曲面，验证了无网格方法在求解位场延拓问题中的可行性。图3给出了模型1中分别采用EFG方法和FD方法得到的磁场空间误差图。由图2、图3可见，相对于FD方法，EFG方法的误差较小，并且相对于FD方法，EFG方法基于点的近似不需要网格的初始划分，减少了计算难度。

图2 EFG方法的数值解磁场曲面Fig.2 Magnetic field surface by EFG method

图3 模型1中EFG方法和FD方法的磁场空间误差Fig.3 Magnetic field space error by EFG and FD method in model 1(a) EFG方法磁场空间误差图；(b)FD方法磁场空间误差图

4.2 理论模型2

有一水平地面测线，同样15个测点信息。地面边界上2号点～9号点磁场为100nT，10号点～14号点磁场为10nT,其余两点磁场为0nT,如图4所示。

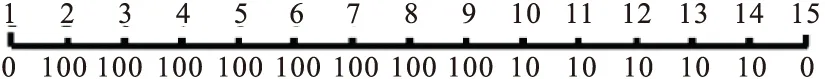
图4 模型2中测点的场值信息
Fig.4 Field value in model 2

将模型2中x方向水平地面长度定为300 m，高度定为600 m。 图4上部空间等间距均匀布置15×29个节点，四个本质边界条件节点上的罚因子取为1015。图5给出了模型2中分别采用EFG方法和FD方法得到的磁场空间等值线。横轴、纵轴分别代表x、z轴的节点编号。由图4可见， EFG方法和有限差分方法的求解的等值线的形态十分相似，并且相对于FD方法，EFG方法的等值线更为光滑。

4.3 实测数据计算

图6给出了一个某地地面上的实测总强度磁异常曲线[14]，该数据包含45个测点的场值信息。由于此地区浅部覆盖有一层磁性较强并且很不均匀的玄武岩，因此磁场出现剧烈的跳动，在该曲线上有两个局部异常。为了消除地区玄武岩的干扰，对该数据进行延拓，采用EFG方法进行数值求解。将求解区域Ω扩展到无穷远边界，下边界的场值采用测量的边界场值按余弦衰减的方式衰减至零[6]。

图5 EFG方法和FD方法磁场空间等值线Fig.5 Magnetic field space contour by EFG and FD method in model 2(a) EFG方法磁场空间等值线；(b) FD方法磁场空间等值线

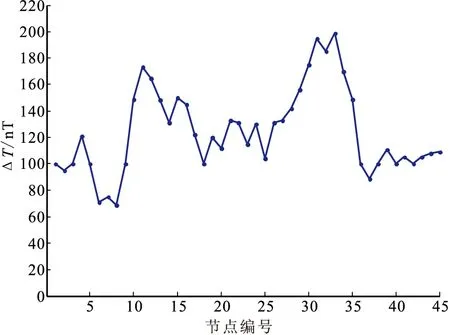
图6 实测数据曲线Fig.6 Curve of the measured data

图7 求解区域Fig.7 Computation domain

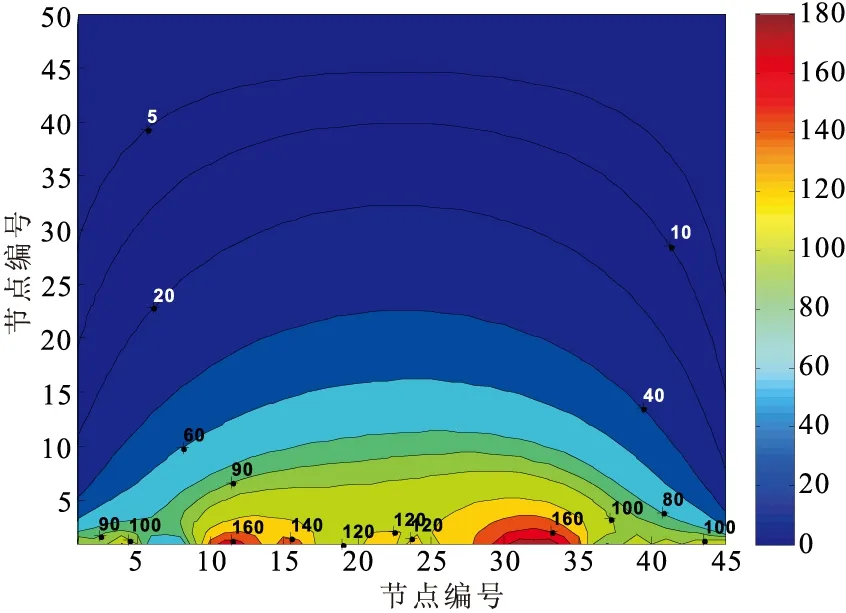
图8 磁场空间等值线Fig.8 Magnetic field space contour

图8给出了采用EFG方法得到的磁场空间等值线。由图8可见,通过位场向上延拓,基本消除了浅部玄武岩这一磁性体的干扰,突出了深部磁性体所产生的磁场。

为了分析在不同高度的磁异常的衰减关系,本文主要选取了三个不同的高度进行分析,分别是向上延拓1个测点距，5个测点距和20个测点距，对不同高度的磁异常强度进行曲线对比,如图9所示。由图9可见，随着高度的增加,异常体磁场衰减很快, 异常体产生磁场的异常也就越不明显。当向上延拓20个测点距时，已分辨不出上述的两个局部异常了,这与实际情况相符。EFG方法的数值模拟结果对研究区域场有重要作用,这也是向上延拓的必要性所在。

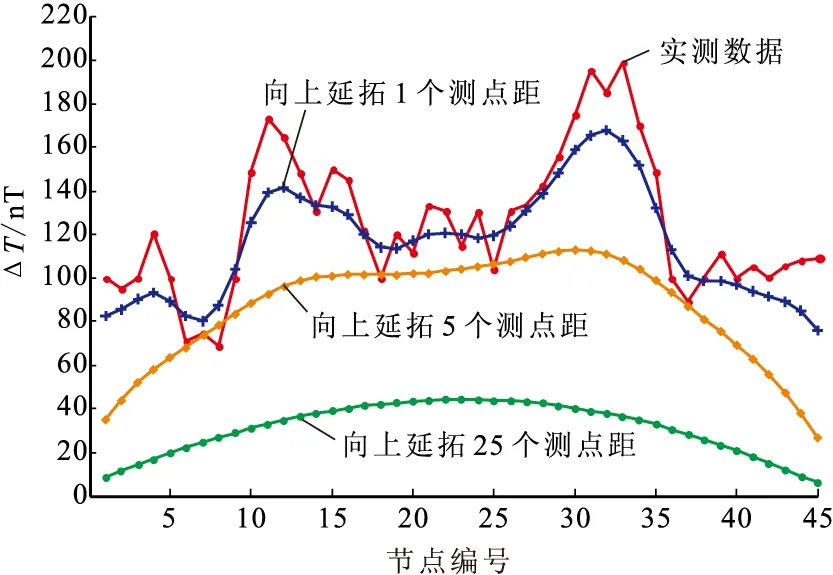
图9 实测总强度磁异常进行向上延拓结果Fig.9 The upward continuation result of the observed data

5 结论

采用EFG方法，对不同模型和实例的二维位场延拓问题进行了数值求解，同时与有限差分(FD)法的数值结果进行了比较。数值结果表明：

1)EFG方法在数值求解过程中，只需输入节点信息和边界条件,减少了有限差分法中复杂的网格生成过程，相对于FD方法，采用EFG方法均能很好地处理二维位场延拓问题，验证了无网格方法在求解位场延拓问题中的可行性。

2)采用EFG方法进行实例求解，数值模拟结果与实际形态趋势基本一致，实现了位场的向上延拓,表明了方法求解位场延拓问题的有效性。

3)无网格方法需要通过背景网格进行高斯积分，并且由于边界条件的特殊处理等问题,使得无网格法目前的计算速度尚低于FD法，因此EFG法在位场延拓问题中的应用还需要更深入的研究。

[1] 邓正栋,关洪军,聂永平,等.稳定地电场三维有限差分正演模拟[J].石油物探，2001,40(1):107-114. DENG ZH D,GUAN H J, NIE Y P，et al. 3D finite difference forward modeling of stable geoeleclrical field[J].Geophysical Prospecting for Petroleum,2001,40(1):107-114. (In Chinese)

[2] 尤淼，鲁霞，张健.有限差分法在二维位场延拓的应用[J].工程地球物理学报，2010,7(3):269-273. YOU M, LU X, ZHANG J. Application of FDM to two-dimensional potential field extension[J]. Chinese Journal of Engineering Geophysics, 2010,7(3):269-273. (In Chinese)

[3] 杨曦，潘和平．井间电磁场时域有限差分数值模拟[J]．地球物理学进展，2008，23(2)：573-682． YANG X, PAN H P. The simulation of cross-hole electromagnetic fields using FDTD method[J]. Progress in geophysucs, 2008, 23(2): 573-682．(In Chinese)

[4] 胡博，岳建华，邓帅奇．边界元算法在电法勘探正演中的应用综述[J]．地球物理学进展，2010，25(3):1024-1030. HU B, YUE J H, DENG SH Q. Review on the forward modelling by the boundary element method in electric exploration[J]. Progress in Geophys, 2010，25(3):1024-1030. (In Chinese)

[5] 郭荣文.磁场的有限元模拟与延拓研究[D].长沙：中南大学，2007. GUO R W. Finite element simulation of magnetic field and extension research[D].Changsha: Central South University, 2007. (In Chinese)

[6] 宋滔,罗勇,王宇航.有限单元法在二维位场延拓中的应用[J].工程地球物理学报, 2012,9(2):134-138. SONG T, LUO Y, WANG Y H. Application of FEM to two-dimensional potential field extension[J]. Chinese Journal of Engineering Geophysics, 2012,9(2):134-138. (In Chinese)

[7] 徐世浙,楼云菊. 起伏地形二维位场上延与换算的边界单元法[J]. 物探化探计算技术,1987,9(3): 195-199. XU SH Z, LOU Y J. Application of the boundary element method to the continuation upward and transformation of 2-D potential field on relief topography[J]. Computing techniques for Geophysical and Geochemical Exploration, 1987,9(3): 195-199. (In Chinese)

[8] 徐世浙,王庆乙，王军.用边界单元法模拟二维地形对大地电磁场的影响[J].地球物理学报，1992,35(3):380-388. XU SH Z, WANG Q Y, WANG J. Modeling 2-D terrain effect on MT by the boundary element method [J]. Chinese Journal of Geophysics, 1992,35(3):380-388.(In Chinese)

[9] 徐世浙．位场延拓的积分-迭代法[J].地球物理学报，2006，49(4)：1176-1182. XU SH Z. The integral-iteration method for continuation of potential fields[J]. Chinese Journal of Geophysics, 2006, 49(4):1176-1182.(In Chinese)

[10]BELYTSCHKO T, LU Y Y, GU L. Element-free Galerkin methods [J]. International journal for numerical methods in fluids, 1994, 37(2): 229-256.

[11]赵光明，宋顺成. 无网格Galerkin法与有限元耦合新算法[J].应用数学与力学，2005，26(8):899-904. ZHAO G M，SONG SH C. New Algorithm of Coupling Element-Free Galerkin and Finite Element Method[J]. Applied Mathematics and Mechanics, 2005,26(8):899-904. (In Chinese)

[12]张小华, 欧阳洁. 线性定常对流占优对流扩散问题的无网格解法 [J]. 力学季刊, 2006, 27(2): 220-226. ZHANG X H, OUYANG J. The element free Galerkin method for steady convection dominated convection- diffusion problem [J]. Chinese Quarterly of Mechanics, 2006, 27(2): 220-226. (In Chinese)

[13]王卫东，赵国群，栾贻国. 无网格方法中本质边界条件的处理[J]. 力学季刊，2002，23(4)：521-527. WANG W D, ZHAO G Q, LUAN Y G. Treatment of essential boundary conditions for element-free Galerkin method[J]. Chinese Quarterly of Mechanics,2002,23(4):521-527. (In Chinese)

[14]谭承泽，郭绍雍．磁法勘探教程[M ]．北京:地质出版社,1984． TAN CH Z，GUO SH Y. Magnetic prospecting guide[M].Beijing: Geological Publishing House,1984. (In Chinese)

第39卷 第2期2017年3月物探化探计算技术COMPUTING TECHNIQUES FOR GEOPHYSICAL AND GEOCHEMICAL EXPLORATIONVol.39 No.2Mar. 2017

Research on element free Galerkin method for 2-D potential field extension

KONG Qian1, LI Peng1, LI Jing2

(1.School of Applied Mathematics and Physics, North China Electric Power University, Zhuozhou 071003, China; 2.BGP,CNPC, Baoding 072751, China)

The upward continuation of potential field can be induced to determine the function for satisfying the Laplace equation. The Element Free Galerkin (EFG) method is extended and employed for numerical computations of 2-D potential field extension. The principle of the EFG method and its numerical implementation are described. The discrete equation of EFG method is built for 2-D potential field extension. The results of our method are compared with that of finite difference (FD) method. Simulation results show that the proposed method and FD method have the same performances. In addition, a practical case is given in this paper. The theoretic and real numerical results show that EFG method is efficient and easy-implementation in solving the problem of potential field extension.

potential field extension; the element free Galerkin method; the finite difference method; forward calculation

2015-12-15 改回日期：2016-02-15

国家自然科学基金项目(11274111);河北省自然科学基金(F2015502014)

孔倩(1981-), 女，博士，主要研究偏微分方程数值解法，E-mail:qiankongkong @126.com。

1001-1749(2017)02-0155-06

P 631.3

A

10.3969/j.issn.1001-1749.2017.02.01