初中数学教学中例、习题的变式及重组

赖秀将

在初中数学教学中开展变式教学，能调动学生的学习兴趣，培养学生的逻辑思维能力，提高课堂教学效果.

下面结合自己的教学实践就初中数学教学中例、习题的变式及重组谈点体会.

一、概念性变式教学

概念变式，即对概念进行多方位的分析理解，利用更加直观的变式介绍概念.初中学生知识体系的建立过程，最重要的就是初期阶段，但是在现有的数学教材中，有很多概念知识都非常抽象，概括性比较强.因此，在概念教学中，教师要利用概念变式进行前后对比，扩展学生的发散性思维，激发学生的学习兴趣，让学生养成自主学习的习惯，使学生直接接受概念经验，打破传统的教师单一传授知识的教学模式，提高课堂教学效果.

例如，在讲“平行四边形法则”和“矩形、菱形和正方形”时，为了让学生理解平行四边形、菱形和正方形之间的联系和关联，教师可以在讲平行四边形的概念时进行概念变式：改变平行四边形的某个内角，可以形成什么特殊的图形？让学生讨论实验，在纸上画出图形后，通过分组讨论，使其中一個内角改为直角，与矩形图形进行对比，引出矩形的概念.同理，由菱形引出正方形的概念.

通过概念性变式教学，在学生原有的认知体系中增加一些条件的变化，使其衍生出新的概念和知识点，在学生学习概念的同时，把抽象的概念变化到具体式子，让学生在比较短的时间里掌握学习新的知识，了解其原始的本质，提高学生的学习效率.

二、定理、法则、公式性变式教学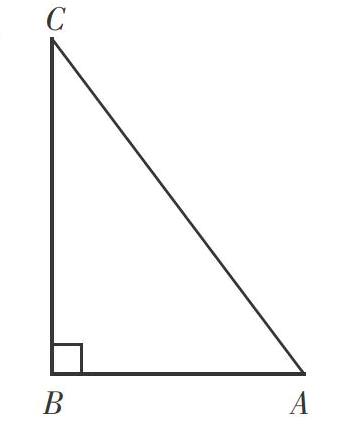

在初中数学教学中，定理、法则、公式等相关概念，处于基础的位置，也是以后学习的重要依据.数学的变式教学体现在定理、公式和法则的推论中，对学生数学能力的培养具有现实意义.

例如，在讲“勾股定理”时，对于“直角三角形三边关系”，有例题如下：如图，在Rt△ABC中，已知∠B=90°，AB=6，BC=8，求AC的长.

变式1：在Rt△ABC中，已知∠B=90°，AB=6，AC=10，求BC的长.

变式2：在Rt△ABC中，已知斜边AC比直角边AB长4cm，一条直角边BC长12cm，求AC的长.

定理、法则和公式的变式教学，能激发学生相互探讨、相互学习的学习热情.传统的公式、定理的教学，通常只是单一、直接地传输知识点，让学生对公式、定理进行死记硬背，不要求学生理解其蕴涵的本质.变式教学就打破了这一点，把原始、基本的公式定理通过推导，形成下一个知识点的内容，让学生更加清楚公式定理的来龙去脉，对于学生掌握知识点具有立竿见影的效果.

三、例、习题的变式与重组

例、习题应该取自于教材，但又不能局限于教材.在研读教材的例、习题时，教师要善于总结例、习题中的规律和出题意图，并根据教学要求和目的，对习题进行升华改造，挖掘例、习题的内在潜力，通过例、习题的变式与重组，使其更加有利于学生的理解和掌握，培养学生对问题的思考能力，以达到培养学生的逻辑思维、开发学生的智力、激发学生的学习兴趣的效果.

例如，教材中习题：有一项工作，甲单独做20小时完成，乙单独做12小时完成.如果两个人一起做，需要多少时间完成？

变式1：甲单独做20小时完成，乙单独做12小时完成.如果甲先单独做4小时，然后乙再加入一起做，需要多少时间完成？

变式2：甲单独做20小时完成，乙单独做12小时完成.如果甲先单独做4小时，然后乙再加入一起做，需要多少时间完成总工作量的2/3？

变式3：甲单独做20小时完成，甲、乙一起做3小时完成工作量的2/5.如果甲先单独做4小时，乙再加入一起做了2小时后甲有事离开，剩下的由乙独立完成，一共需要多少时间完成工作？

在原有习题的基础上进行变式，一题多变，增加题目考虑的影响因素，逐渐加大难度，能引导学生深入思考，有利于培养学生的逻辑思维能力.

综上所述，初中数学教学中，例、习题的变式及重组，能提高学生的学习效率.教师要重视培养学生的自主学习意识，促使学生自主探索定理概念的本质和它们之间的联系.

（本文是泉州市教育科学“十三五”规划（第一批）立项课题《初中数学教材例习题“二次开发”策略研究》（立项批准号： QG1351-211）的研究成果.）