教学中提高学生素质的策略研究
江苏省扬州市江都区郭村中学(225239)
田中华●
教学中提高学生素质的策略研究
江苏省扬州市江都区郭村中学(225239)
田中华●
本文从3个方面谈学生个体成长规律:①要培养起创造师生之间和谐合作的教学氛围;②尊重学生的个体成长规律,因材施教;③培养学生真诚、坚持不懈尊重事实的正确学风.本文第二部分指导学生掌握好基础知识,本文第三部分指出在学习中要研究方法.
和谐合作的教学氛围;尊重学生成长规律;正确学风;一元二次方程解法;研究方法
一、对学生个体成长规律要有明确认识
中国传统文化重视道,即客观规律,经营有经营之道,做人有做人之道,同样教学有教学之道.教学之道在于人效法天地自然的运动变化规律,因人施教.
(1)创造师生之间和谐、合作的教学氛围.
课堂上师生的配合是建立在相互理解的基础上.教学是教师与学生“教”与“学”的双向互动.既然是一种互动,那就必然要牵扯涉到如何处理互动双方也就是师生之间的关系,和谐的师生关系是教学的理想状态.课堂上师生的配合是建立在相互理解的基础上.
(2)尊重学生的个体成长规律,因材施教.
《论语·为政》朱熹集注中:“子游能养而或失于敬,子夏能直义而或少温润之色,各因其材之高下与其所失而告之,故不同也.”这是因材施教的最早出处.著名教育家陶行知曾经说过:培养教育人和种花木一样,首先要认识花木的特点,区别不同情况给以施肥、浇水和培养教育,这叫“因材施教”.因材施教是在尊重学生身心发展规律的基础上进行教学的方式.一定年龄学生,他们的心理特点和智力水平既有一定的普遍性,又有一定的特殊性,教学中针对学生的共同特点和个别差异,因材施教,有利于扬长避短,长善救矢.教师通过受课和课下与学生交流,充分了解学生的知识水平、接受能力、学习风气、学习态度和每个学生的兴趣、爱好、知识储备、智力水平以及思想、身体等方面的特点,以便从实际出发,有针对性地教学,教学中既要侧重全体,又要兼顾个体.
(3)培养学生真诚、坚持不懈、尊重事实的正确学风.
现代科学技术的发展瞬息万变、一日千里.各种新思潮、新理论层出不穷,怎样学会分辨真伪、善于取舍,变他物为我物,需要培养学生的科学精神.“科学精神包括:怀疑一切既定权威的求实态度,对理性的真诚信仰,对知识的渴求,对可操作程序的执着,对真理的热爱和对一切弄虚作假行为的憎恶,对公正、普遍、创造等原则的遵循.可以毫不犹豫地说,它们无不是人类精神中最深层次的内涵.在这一层次上,所谓科学精神与所谓人文精神——对交流和互动方面,教学才能切入学生的经验领域,课堂才能成为师生互动的空间,才能引导学生主动学习.
二、掌握好基础知识
万丈高楼平地起,任何知识宝库都是由点点滴滴知识组成一元二次方程与二次函数是学习数学的基础,也是初中数学的重点,学习一元二次方程和二次函数章节就要掌握好如下基础知识点.
1.一元二次方程
一元二次方程只含有一个未知数,且未知数的最高次数是2的整式方程叫做一元二次方程.
一般式:ax2+bx+c+0(a≠0).其中ax2叫做二次项,a是二次项的系数;bx叫做一次项,b是一次项的系数;c叫做常数项.在一元二次方程中,b、c可以是任意实数,但二次项的系数a是不为零的实数.因为a=0时,这个方程就不是一元二次方程.
2.一元二次方程的根的判别式
根的判别式,我们把b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0)的根的判别式,用符号“Δ”表示.
一元二次方程ax2+bx+c=0(a≠0);
当Δ>0时,方程有两个不相等的实数根;
当Δ=0时,方程有两个相等的实数根;
当Δ<0时,方程没有实数根.
所以已知一元二次方程根的情况,根据根的判别式可以确定方程中字母系数的取值范围.
3.一元二次方程的根与系数关系
如果方程ax2+bx+c=0(a≠0)的两个根是x1,x2,那么x1+x2=-b/a,x1·x2=c/a.
4.二次函数
一般的函数y=ax2+bx+c(其中a、b、c是常数,a≠0)叫做关于x的二次函数.
二次函数的定义域是一切实数,但在实际问题中,还必须使实际问题有意义.
5.二次函数的图象和性质
①抛物线:二次函数y=ax2+bx+c(a≠0)的图象,我们把这个图象叫抛物线.一般的,抛物线y=a(x+m)2+k的对称轴是过点(-m,0)且平行于y轴的直线(即直线x=-m),顶点坐标是(-m,k),当a>0时,抛物线开口向上,当a<0时,抛物线开口向下.②配方法:把二次函数y=ax2+bx+c用配方法改写成y=a(x+m)2+k的形式,当a=1时,与解一元二次方程的配方法相同;当a≠1时,与解一元二次方程的配方法不同,必须提取公因式a而不是用a除二次三项式的各项,二次函数写成配方式后就可确定它的顶点和对称轴了.
三、要研究解题方法
只有研究方法才能做到举一反三.举例如下:
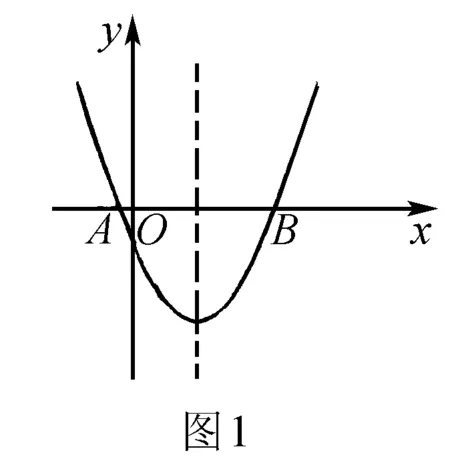
例题 如图1,已知二次函数y=x2+bx+c的图象的对称轴是直线x=1,且图象与x轴的两个交点间的距离为4.求这个二次函数的解析式.
分析 解法1 因为抛物线是一个轴对称的图形,所以由对称轴是直线x=1及图象与x轴的两个交点间的距离为4,可以知道,抛物线与x轴的两个交点分别为A(-1,0)和B(3,0).可以利用交点式进行求解,而已知a=1.所以此二次函数的解析式为y=(x+1)(x-3),即y=x2-2x-3.
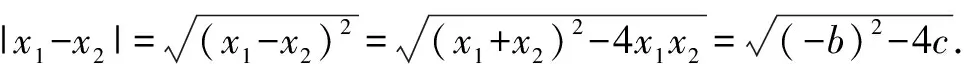
所以此函数的解析式为:y=x2-2x-3.
说明 解法2中利用了一元二次方程根与系数的关系将抛物线与x轴的两个交点间的距离是4转化成为含系数b、c的方程.
G632
B
1008-0333(2017)11-0007-01

