研究解题方法 培养反思习惯

江苏省扬州市邗江区陈俊学校(225116)

刘庆金●



研究解题方法 培养反思习惯

江苏省扬州市邗江区陈俊学校(225116)

刘庆金●

本文强调解题后必要反思养成反思习惯，特别是反思解题方法关于解题方法文中以举实例详谈了利用判别式法、配方法、换元法、逐步调整法以提高学生的解题能力，培养创新思维.

判别式法；配方法；换元法；逐步调整法

每解完一个数学题一定养成反思习惯，特别是反思解题方法，就解题而方应追求简单自然的解法，不必“为技巧而技巧”，舍近求远.下面就教学实践中常用的几种方法举例研究供参考.

一、利用判别式

利用判别式解整系数一元二次方程的整数根问题有下列常见的切入方式：(1)有整数根的前提是有实数根，则△≥0，确定参数的取值范围；(2)有整数根必定有有理根，则Δ必为完全平方数；(3)若判别式是关于参数的一次式，则可设其为t2(t为非负整数)，再将方程的根用t表示(见例1解法2)).

例1 (“祖冲之杯”竞赛题)试求出所有这样的正整数a，使得二次方程ax2+2(2a-1)x+4(a-3)=0至少有一个整数根.

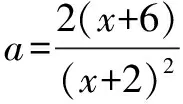
解法2Δ=4[(2a-1)2-4a(a-3)]=4(8a+1)为完全平方数，故8a+1为奇数的平方.

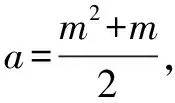
二、配方法

配方法的作用在于揭示式子的非负性，是挖掘隐含条件的有力工具；配方法的实质在于改变式子的原有结构，是变形求解的一种手段，配方法在解代数式化简求值、求最值、解不定方程等方面有广泛的应用.

例2 求方程8(2x2+6x+6)(3y2-3y+2)=15的解(x,y).

分析与解 能展开吗？不妨应用配方法，从估算两个因式的值的取值范围切入.

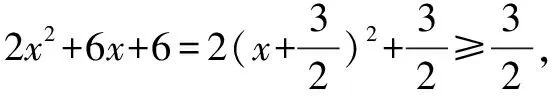
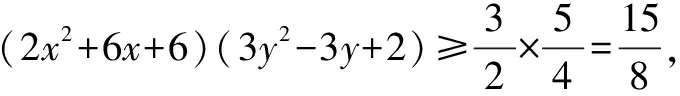
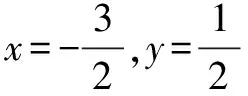
三、换元法

玻利亚在“怎样解题”表中的许多问句都是以转换问题为目的，如：你知道与它有关的问题吗？你能想出一个相同或相似的熟悉问题吗？你能改述问题吗？

你能不能用不同的方法重新叙述它？

换元是建立在观察基础上的，换元不拘泥于一元代换，可根据问题的特点，进行多元代换.

方程②：(u+v)2-2uv=13代入①

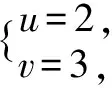
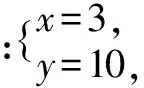
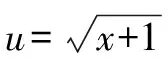
四、逐步调整法

逐步调整法是解离散最值问题的有效方法，即先通过逐步调整变量之间的关系来找出取到最值所需满足的必要条件，然后再求最值.

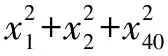
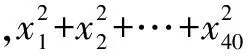
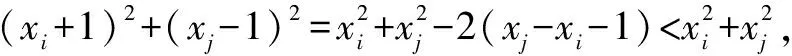
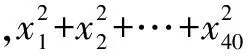
G632

B

1008-0333(2017)11-0005-01