培养学生“论说”·“反思”·“创新”能力的教学探讨

江苏省扬州市邗江区方巷镇中心中学(225117)

谢 丹●



培养学生“论说”·“反思”·“创新”能力的教学探讨

江苏省扬州市邗江区方巷镇中心中学(225117)

谢 丹●

本文论述了在数学教学中，培养学生“论说”，“反思”，“创新”能力的方法和策略.

数学教学；论说；反思；创新；能力

《数学课程标准》告诉我们：数学教学不仅要考虑教学自身的特点，而且要遵循学生学习数学的心理规律，让学生亲身经历数学问题的解释与应用，并能在探索的过程中形成自己的观点，能在倾听别人意见的过程中逐步完善自己的想法，实现“不同的人在数学上得到不同的发展”.根据这个观点在数学教学中要让学生学会“论学”、“反思”、“创新”，让学生在数学学习过程中建构自己的数学知识技能，获得对数学的理解、应用、发展的能力.

一、让学生学会“论说”

在这里所指的“说”包括：(1)“读”数学课本“读”数学问题.通过“读”让数学概念和数学问题在学生大脑中有一个初步的印象；通过“读”让学生对数学问题有一个感性的认识，从而为上升到理性认识打好基础.

(2)“说”数学问题中的关键字词(条件)，关键数据的含义.每个数学问题中都有该问题的关键字词，让学生“说”出它，可以看出学生对问题的理解是否已经抓住了重点，有没有分清主次；“说”关键数据，可以让学生从众多的数据中梳理出解决问题所需的数据，以及它所代表的量的含义，防止错用和乱用.

(3)“论说”解题思路，让学生说出自己的解题思路，从而把他的想法暴露于大家面前，一者可以培养学生敢说的胆量，为以后敢问打下基础，二者可以让教师和学生共同发现学生思维的优点和缺陷，从而优化解题思路，三者还可以对该问题的探究可续性提供宝贵素材，提倡提出不同见解可以争论.

这里所说的“争论”不是平常所指的吵架，而是指学生在数学思想和方法方面进行的探讨和辩论.俗话说：三个臭皮匠顶个诸葛亮.一个班级中一般有学生四、五十个，教师由于年龄、经验等因素，这个“诸葛亮”往往难免会有失策的地方，而四、五十个“臭皮匠”有时会胜过“诸葛亮”.所以，在课堂教学中，教师要充分发现和利用这样的机会，让学生有机会“斗”，通过“斗”让学生之间互相发现各自薄弱的一面，展示他们的能力和才华，在共同学习中提高数学解决问题的能力.

二、让学生学会“反思”

解题后，回顾解题过程中所用到的基础知识，基本技能等，有利于温故知新，有利于提高分析问题解决问题的能力.

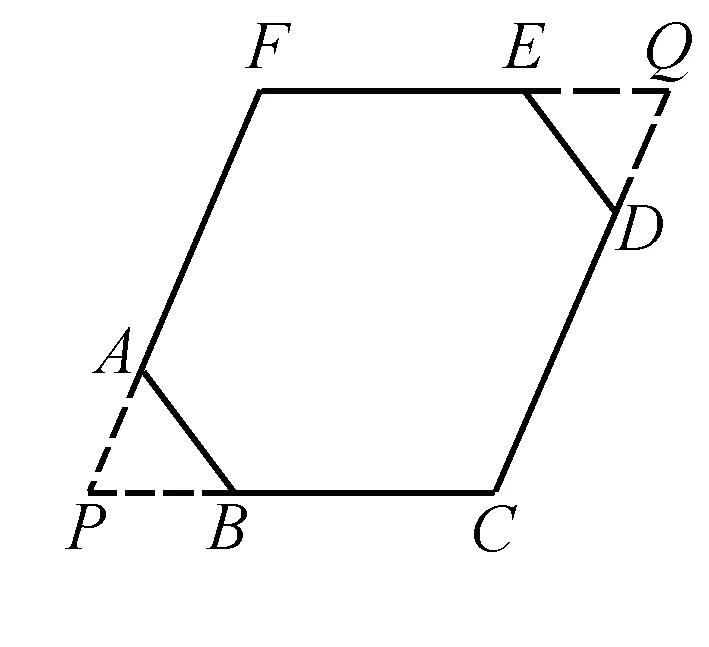
例1 如图，六边形ABCDEF中，若∠A=∠B=∠C=∠D=∠E=∠F,且AB+BC=11，AF-CD=3，则BC+DE等于多少？

解析 由已知∠A=∠B=∠C=∠D=∠E=∠F可知这些角均为120°，于是延长FA、CB交于点P，延长FE、CD交于点Q，则得△ABP和△EDQ均为等边三角形.由∠F=∠C和∠P=∠Q得四边形FPCQ为平行四边形，则PA+AF=CD+DQ，即AF-CD=DQ-FA=DE-AB.又已知AF-CD=3，则得DE-AB=3①.又AB+BC=11②，将①、②两式相加可得BC+DE=14.

反思 本题通过构造平行四边形并利用平行四边形的性质得出AF-CD=DE-AB=3，再将其和已知条件AB+BC=11相加，巧妙地得出欲求式子的值.

三、让学生学会“创”

所谓“创”就是指创新、探究.《数学课程标准》中指出：数学教学要体现现代教育观念，重视学生创新能力，突出问题解决在数学教学中的重要性….而课堂教学正是让学生学会“创”的理想场所.当然，作为初中学生虽然独立思考和探索的愿望和能力均需再提高，但教师作为组织学生“创”的引导者和组织者，首先自己要有“创”的意识，同时有必要给学生提供“创”的条件和素材，在潜移默化中让学生自己逐步学会“创新”.让学生学会“创”，可以从以下几个方面考虑：(1)对于同一问题，让学生思考能否用其他方法来解决，即我们所说的一题多解即方法上“创”.(2)对于同一问题，改变问题的条件让学生思考能否得到原来的结论即条件上“创”.(3)对于同一问题，不改变问题的条件让学生思考能否得出其他结论即结论上“创”.(4)对于同一问题，如果用其他图形替代原来图形(如用四边形替代三角形)，结论又如何？即横向“创”.(5)对于同一问题，如果改变原来条件或形状，又能联想到什么？纵向“创”.

①逆向变形

解分式方程的传统思想方法是通过去分母或换元把它化为整式方程来解，对于特殊的四次整式方程，也可以反过来化为分式方程来解.

例2 解方程6x4+5x3-38x2+5x+6=0.

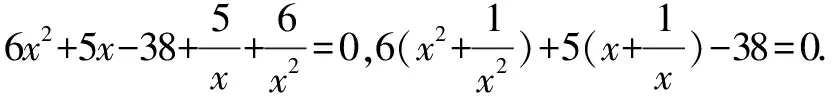
②巧用反证

G632

B

1008-0333(2017)11-0003-01