钛合金耳片的静载失效分析与结构优化研究*

李 辉，陈 蓬，姚泽坤，宁永权

（1. 中国航空工业第一飞机设计研究院，西安 710089；2. 西北工业大学材料学院，西安 710072）

钛是20世纪50年代发展起来的一种重要的结构金属。钛合金因比强度高、耐蚀性好、耐热性高等特点而被广泛用于航空、航天、舰船、核能、电力、交通等领域[1-6]。飞机在襟翼滑轮架侧板、铰链接头、基座等结构部位采用钛合金零件，其中部分零件涉及到耳片连接结构[7-9]。目前，钛合金耳片的效率系数曲线不全。为了对钛合金耳片进行强度分析和结构优化，开展本试验研究，以获得直耳片且耳片尺寸的比值b/d分别为1.5、2.0、2.5、3.0s，c分别为1.0、1.2、1.4、1.6时，不同加载角度（0°、30°、60°、90°）的拉伸破坏载荷数据；探索耳片尺寸对效率系数K0及折算系数Kcon1的影响规律；通过断口观察、成分分析、组织检验等理化测试，确定耳片的断裂性质及失效原因。

1 试验及方法

1.1 耳片结构设计

采用ABAQUS软件对钛合金耳片静载荷拉伸进行了有限元模拟，以优化耳片结构。为保证组合耳片经过3次加载而不变形，对中间进行增厚设计。中部采用试样厚度t=9mm，3个测试耳片采用t=6mm。对设计方案进行有限元分析验证，30°、60°、90°加载的验证结果如图1所示。本模型中，耳片采用带厚度参数的平面单元，销钉采用解析刚体。在左上角公共加载孔销钉处施加位移边界条件，在左下角耳孔销钉处施加载荷，载荷方向沿公共加载孔和耳孔中心连线向外。销钉与孔之间通过无摩擦接触面传递载荷。计算时采用基于合金弹塑性分析的计算方法。

加载角分别为30°、60°、90°，耳片部位应力接近母材强度极限时，承力主板部位的应力水平均低于其屈服极限。这说明耳片发生破坏时，承力主板并未发生塑性变形。另外，可以看到在耳片与承力主板连接处有较高水平的应力集中，这是由于在有限元模拟过程中采用的是带厚度的平面单元，耳根处在厚度方向并没有引入圆弧过渡所致。在实际加工时，需要在耳根部位在各方向增加过渡圆弧，以减小此处应力集中，确保试验的有效性。

1.2 试验方法

试验开始前，首先对不同规格的耳片试验件的表面质量进行详细检查，并记录缺陷位置、缺陷尺寸等。对于不符合要求的试验件应剔除并重新加工，以保证试验的顺利进行。

为了试验程序更具条理化和试验数据记录、整理和分析方便，对所有的试验件进行了分类和编号。用计量检定合格的游标卡尺及内测千分尺测量耳片的几何尺寸，包括耳片宽度b、厚度t、耳孔直径d以及耳高H；测量过程中不得损伤试样表面。钛合金耳片拉伸测试严格执行HB5143-1996《金属室温拉伸试验方法》，拉伸速率为3mm/min，加载角度α分别为0°、30°、60°、90°。记录耳片的破坏载荷Pb。选取典型耳片断口，超声波清洗后，利用扫描电子显微镜观察断口形貌并进行失效分析。

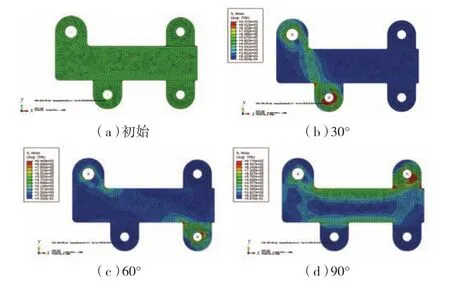
图1 直耳组合耳片有限元模拟Fig.1 Finite element analysis of the titanium alloy lugs processed after static-load tests

2 结果与讨论

2.1 耳片尺寸对破坏载荷的影响

加载角度α=0°时，耳片尺寸对轴向加载破坏载荷的影响如图2所示。可见，耳宽b一定时，破坏载荷随着耳高的增加而增大，且破坏载荷与耳高近似呈线性相关。随着耳宽的增大，直线斜率增大，表明耳高对提升直耳片轴向加载破坏载荷的作用随着耳宽的增加而增大。耳宽的增加会直接增加耳片的承力面积，从而提升耳片的承载能力，故此耳片破坏载荷随着耳宽的增加有较大幅度的增加。

角度加载破坏载荷与耳片几何尺寸和加载角度的关系如图3所示。破坏载荷随着耳宽b的增加有明显的增加，且破坏载荷和耳宽同样呈近似的线性关系。直线的斜率随着加载角度的增加有所降低，这表明在试验范围内，耳片宽度对直耳片斜向加载破坏载荷的提升作用随着加载角度的增加略微有所下降。此外，直耳片角度加载时，破坏载荷随着加载角度的增加有所下降，且下降的幅度随着耳宽的增加而增大。

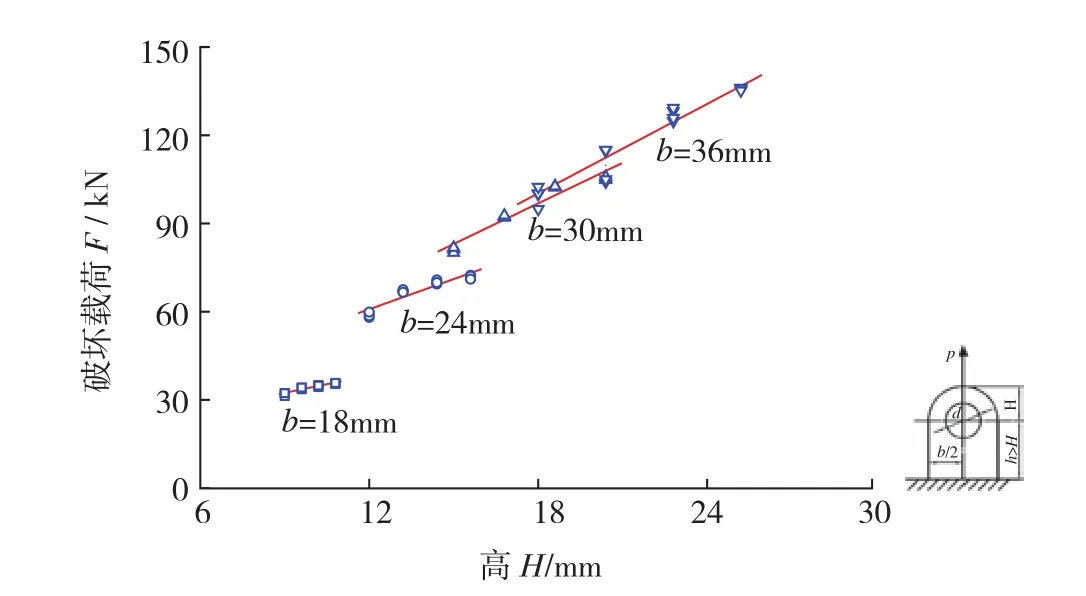
图2 耳片尺寸对轴向加载破坏载荷的影响Fig.2 Effect of lug shape on axial failure load

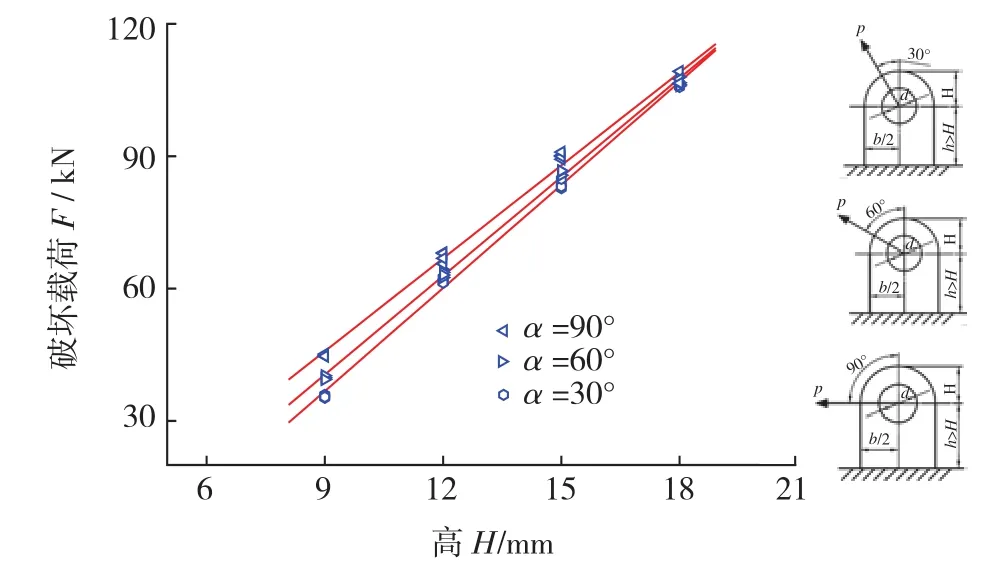
图3 耳片尺寸对角度加载破坏载荷的影响Fig.3 Effect of lug shape on failure load at different angles

2.2 耳片尺寸与加载角度对效率系数的影响

耳片轴向加载按照公式（1）计算效率系数[10]。

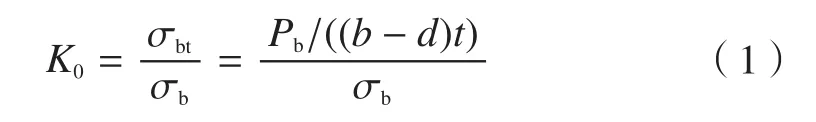
式中，K0为耳片效率系数；σb为材料标准试样所测得的强度极限；Pb为耳片试验破坏载荷；b为耳片宽度；d为孔径；t为耳片厚度。

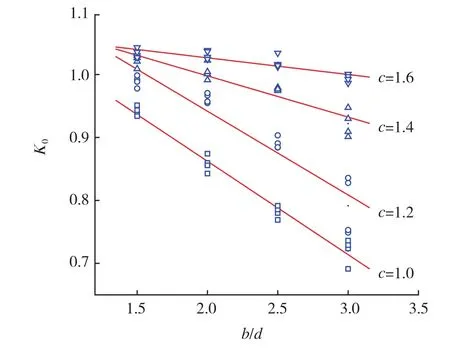
图4 钛合金耳片效率系数K0Fig.4 Efficiency coefficient K0 of titanium alloy lugs

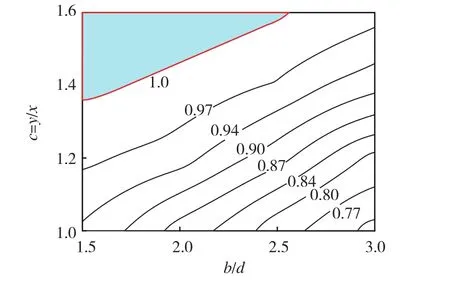
图5 效率系数K0分布图Fig.5 Efficiency coefficient map

耳片效率系数曲线如图4所示，效率系数和b/d有较好的线性关系。图5为直耳片效率系数分布图，当剪切断裂c值和b/d的值位于图中阴影区域内时，耳片的效率系数大于1，且分布非常规律，由此排除了材料组织性能不均匀的影响因素。缺口强化是指缺口试样的破坏载荷与截面积之比大于光滑试样的破坏载荷与截面积之比。缺口强化效应经常发生在具有缺口的塑性材料的试验件上。本试验中的耳片即属于缺口试样，其中的耳片可以认为是缺口。因此，由耳孔引起的缺口强化很可能就是造成直耳片效率系数大于1的原因。

直耳片α角度加载按照公式（2）计算效率系数

式中，Kcon1为加载角度α的折算系数；Pfα0为加载角度α的破坏载荷；Pf00为相同规格的耳片00方向加载时的破坏载荷。

加载角度对直耳片折算系数Kcon1的影响见图6。可见，直耳片的折算系数Kcon1基本小于1。随着加载角度由30°增大至90°，折算系数Kcon1显著减小。因此，在结构设计时，需结合实际工作状态，设计耳片形状与尺寸，避免失效。

2.3 钛合金耳片的失效分析

2.3.1 典型破坏方式

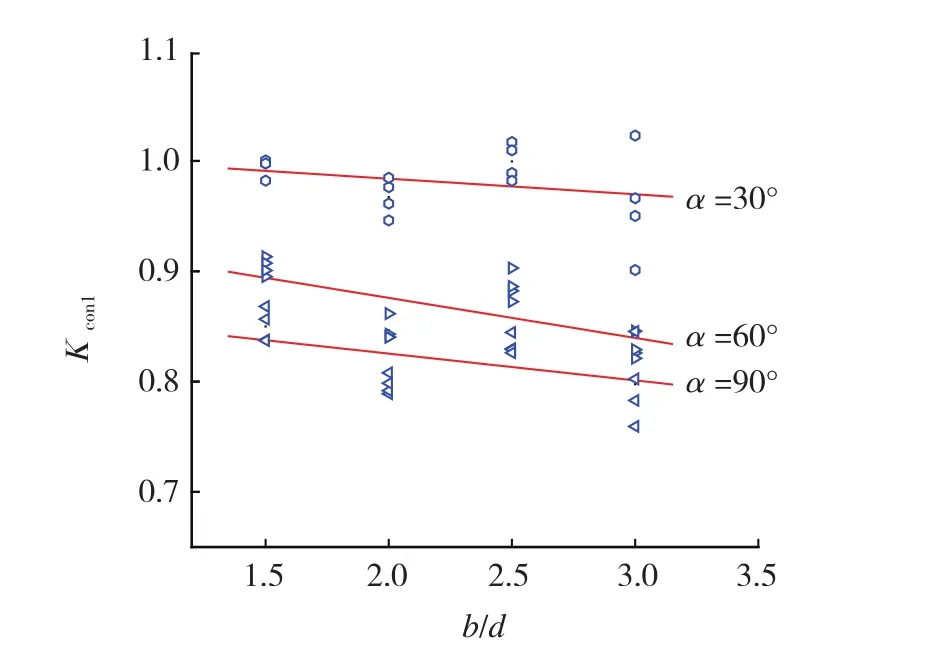
图6 加载角度对耳片折算系数Kcon1的影响Fig.6 Effect of loading angle on Kcon1 of lug

耳片连接件结构简单，但耳孔周围的应力状态却非常复杂。在外力作用下，其头部处于拉伸、弯曲和剪切复合受力状态之下。因此，耳片在轴向载荷作用下，会出现如下3种典型的破坏形式。

拉伸破坏：耳片拉伸净断面远小于剪切面，耳片以拉断为主。

剪切破坏：耳片拉伸净断面远大于剪切面，耳片以剪断为主。

拉剪复合破坏：耳片拉伸净截面与剪切面差别不大，耳片呈拉剪复合破坏形式。

此次耳片静力拉伸试验中直耳片试验件破坏形式出现了4种，如图7所示。

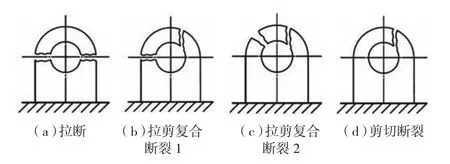
图7 耳片轴向受载破坏形式示意图Fig.7 Diagrammatic failure mode of the titanium alloy lugs

不同尺寸直耳片的破坏形式见表1，其规律归纳为：

（1）当b/d=1.5，耳片断裂方式全部为拉断；

（2）当b/d=2.0，c=1.0、1.2时，耳片断裂方式为拉剪复合断裂；c=1.4、1.6时，耳片断裂方式为拉断；

（3）当b/d=2.5，c=1.0、1.2、1.4时，耳片的断裂方式主要为拉剪复合断裂；c=1.6时，耳片断裂方式为拉断。

（4）当b/d=3.0，c=1.0、1.2、1.4、1.6，耳片的断裂方式主要为拉剪复合断裂，个别试验件为剪切断裂。

综上，随b/d和c的增大，耳片剪切面积增大，破坏形式由拉断为主逐渐转变为拉剪复合断裂，并个别试验件出现剪切断裂，基本符合耳片经典破坏规律。

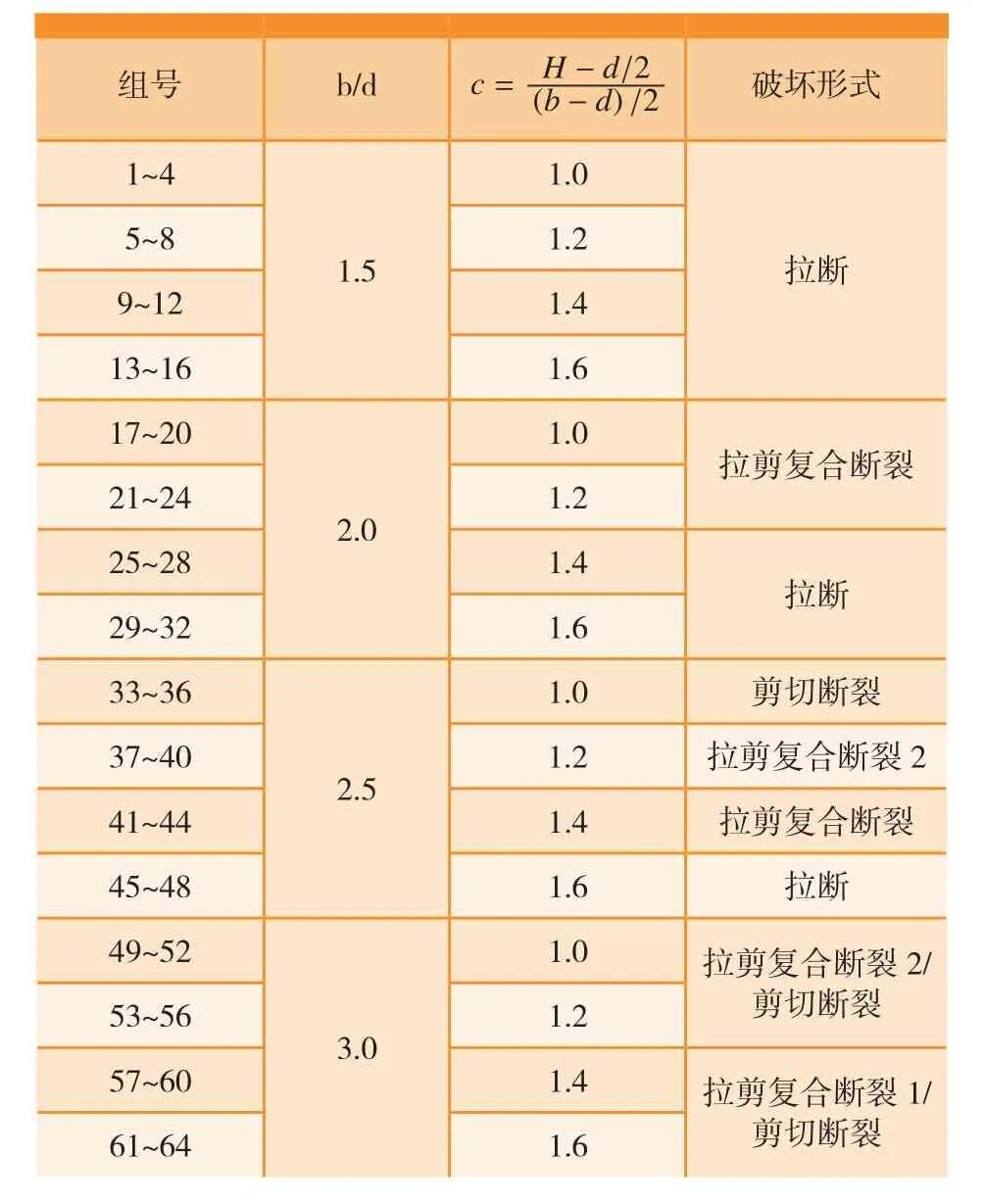
表1 耳片受轴向载荷破坏形式统计表

2.3.2 典型断口形貌

按照断裂应变分类，断裂可分为脆性断裂和韧性断裂。材料或构件断裂前没有宏观塑性变形或塑性变形很小，称之为脆性断裂，其断裂前应变很小；材料或构件断裂前有明显的塑性变形，称之为韧性断裂，其断裂应变较大。从宏观形貌来看，韧性断口一般分为杯锥状或双杯锥状、凿峰状、纯剪切断口等。

图8是直耳片受轴向载荷时，拉伸破坏及拉剪复合破坏拉伸侧的断口形貌。根据断口的低倍照片，可以发现其断口形貌呈现出“杯锥”状形貌，且断口附近有明显的塑性变形。由此可以确定直耳片轴向受载时，拉伸破坏及拉剪复合破坏拉伸侧的断裂均属于韧性断裂。

直耳片轴向加载时，拉伸破坏及拉剪复合破坏拉伸侧的微观断口形貌主要是等轴韧窝。韧窝的形状主要取决于应力状态，与构成韧窝源的第二项质点或母材的塑性变形特征几乎没有关系。等轴韧窝是在正应力作用下形成的。如前所述，直耳片轴向受载类似于单轴拉伸，此时耳片试样中产生的微孔沿空间3个方向的长大速率相同，由此形成等轴韧窝。

图9是剪切破坏断口及拉剪复合破坏剪切侧断口形貌。纯剪切断口也是一种常见的韧性断口，其色泽比较光亮，且断口附近也能观察到明显的塑性变形痕迹。由图9可知，耳片剪切破坏断口的微观形貌主要为剪切韧窝，又称为拉长韧窝。它是在剪切应力作用下形成的，呈抛物线状，并且两个匹配断口表面上韧窝的拉长方向相反。

3 结论

（1）揭示了TC4钛合金耳片几何尺寸与加载角度对破坏载荷的影响规律。

（2）计算获得TC4钛合金轴向加载效率系数K0与角度加载效率系数Kcon1。

（3）对典型断口进行了形貌观察，探讨了钛合金耳片在室温静载荷作用下的断口形貌及其形成机制。

图8 钛合金耳片拉伸破坏断口形貌Fig.8 Typical fracture morphology of the titanium alloy lugs processed after static-load tests

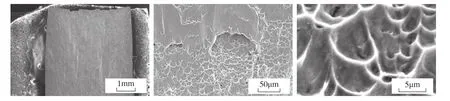
图9 钛合金耳片剪切破坏断口形貌Fig.9 Shear failure fracture morphology of the titanium alloy lugs

[1]LIANG H Q, NAN Y, NING Y Q, et al. Correlation between strain-rate sensitivity and dynamic softening behavior during hot processing[J]. Journal of Alloys and Compounds, 2015,632:478-485.

[2]NING Y Q, XIE B C, FU M W, et al. Microstructure and superplastic deformation for aerospace Ti-alloys associated with α-phase curing behavior[J]. Aerospace Science and Technology, 2015,45:416-421.

[3]NAN Y, NING Y Q, LIANG H Q, et al. Work-hardening effect and strain-rate sensitivity behavior during hot deformation of Ti-5Al-5Mo-5V-1Cr-1Fe alloy[J]. Materials & Design, 2015, 2:84-90.

[4]LIANG H Q, GUO H Z, TAN K, et al. Correlation between grain size and flow stress during steady-state dynamic recrystallization[J].Materials Science and Engineering: A, 2015,638:357-362.

[5]QIN C, YAO Z K, LI Y Z, et al. Effect of hot working on microstructure and mechanical properties of TC11/Ti2AlNb dual-alloy joint welded by electron beam welding process[J]. Transactions Nonferrous Metals Society of China, 2014,24(11):3500-3508.

[6]TAN L J, YAO Z K, NING Y Q, et al. Effect of isothermal deformation on microstructure and properties of electron beam welded joint of Ti2AlNb/TC11[J]. Materials Science and Technology, 2011,27(9):1469-1474.

[7]刘翠云, 李焕喜, 马朝利. TC18钛合金耳片的断口形貌及疲劳性能[J]. 中国有色金属学报, 2010,20(1):1050-1054.LIU Cuiyun, LI Huanxi, MA Chaoli. Fractograph and fatigue behavior of TC18 titanium alloys lugs[J]. The Chinese Journal of Nonferrous Metals,2010,20(1):1050-1054.

[8]吴根林, 邓承佯, 朱成香, 等. TC4钛合金飞机耳片锻件失效分析[J]. 热加工工艺, 2016,45(1):251-253.WU Genlin, DENG Chengyang, ZHU Chengxiang, et al. Failure analysis on TC4 Titanium ear forging for airplane[J]. Hot Working Technology, 2016,45(1):251-253.

[9]董唯莉, 朱海银, 赵云. TC4钛合金耳片断裂原因分析[J].失效分析与预防, 2012,7(1):46-49.DONG Weili, ZHU Haiyin, ZHAO Yun. Fracture analysis of TC4 titanium alloy ear plate[J]. Failire Analysis and Prevention, 2012,7(1):46-49.

[10]解思适. 飞机设计手册（第9册）[M]. 北京: 航空工业出版社, 2001:654-659.XIE Sishi. Aircraft design manual (volume 9)[M]. Beijing: Aviation Industry Press, 2001:654-659.