不分离型超声复合铣削系统稳定性研究*

（河南理工大学机械与动力工程学院，焦作 454000）

高速铣削加工具有加工精度高、加工表面质量好、生产效率高等优点，被广泛应用在国防、航空航天、模具、汽车等高技术制造领域。在铣削加工过程中，由于相邻两刀齿之间的切削位移存在一定相位差，引起瞬态切削厚度发生变化，进而引起自激振动，最终导致切削颤振。颤振严重影响着工件表面质量、机床加工效率和刀具寿命，这对于高速加工来说，更为显著。因此，提高切削系统稳定性是提高加工精度和效率的重要方法之一。目前，在铣削加工过程中，避免加工颤振的研究主要分为合理使用稳定性极限图[1]和提高铣削系统的稳定性[2]。

合理使用稳定性极限图主要是通过建立轴向切削深度与主轴转速之间函数关系式，利用Floquet理论，将稳定性极限图分为切削稳定区和非稳定性区[1]，从而选择合适的加工参数，使铣削系统工作在切削稳定区。为预测加工系统稳定性极限，许多学者进行了大量的研究。Altintas等利用频率法进行铣削系统稳定预测，提高了稳定性叶瓣图预测的精度[3-4]；Insperger等[5]利用两相邻离散的时滞项进行加权处理，提出了新型半离散法；Ding等[6]利用直接积分法提出一种有较高计算效率的全离散法。在上述方法中，由于需要做大量的试验以验证所提理论的正确性，并且不能提高系统的稳定性，导致经济性差等缺陷。

提高铣削系统稳定性的方法主要有：超声加工法[7]、智能控制法[8]、变刀具几何角度法[9]和主动控制法[10]等。超声加工法有别于其他的方法，它改变了传统切削方式，是一种新型提高切削系统稳定性的方法[2]。皮均等[11]对纵扭共振超声铣削不锈钢进行了研究，结果表明纵扭共振超声旋转加工可大幅提高加工效率；唐军等[2]考虑了交叉传递函数对超声复合铣削系统稳定性的影响，并通过铣削加工碳纤维复合材料(C/C)进行试验验证，但是纵扭超声复合铣削方法对变幅杆形状要求较高。

超声加工是一种精密超精密加工的方法，在航空航天、国防和化工等领域得到了日益广泛的应用[11]。其速度系数K是一个非常重要的参数。当K≥1时，超声复合铣削加工属于不分离型加工，反之则属于分离型加工。分离型超声复合铣削加工已经被证明能提高铣削系统的稳定性[2,11]，然而不分离型对铣削系统的稳定性的影响，目前研究的较少；另外，关于采用半离散法是否能预测超声复合铣削系统稳定性的研究，也鲜见报道。因此，本文基于现有的超声振动装置，提出超声振动铣削模型，分析超声复合铣削加工过程中刀尖的运动特性；基于半离散法建立超声复合铣削系统的稳定性模型，应用MATLAB软件进行数值分析并得出超声铣削稳定性叶瓣图。最后对超声复合铣削系统稳定性模型的正确性进行试验验证。

1 超声铣削系统的运动学分析

由于超声振动施加在工件上，并且与刀具进给方向平行，所以刀尖的运动方程为：

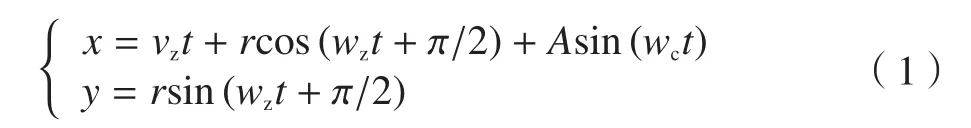
式中，vz是刀具进给速度；r是铣刀半径；wz是主轴角速度；wc是超声波发生器角频率；A是超声振幅。

根据方程（1）可知，此时刀尖速度：

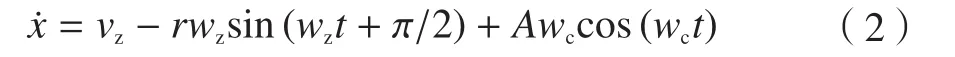
在超声加工中，刀尖与工件高频切削分离的极限条件是vc≥2πAf，vc为临界切削速度，f为超声波振动频率。

由文献[12]可知，工件沿系统进给方向超声振动时，刀具与工件发生切削分离还要满足的必要条件是：λ为奇数，A＞fzs/2，其中λ为wc/wz，fzs为超声铣削系统进给量。

相临齿间运动轨迹仿真见图1，其中Ω是转速。

2 超声铣削系统稳定性模型

超声振动施加在工件上，考虑切削时的再生效应，超声振动铣削系统可以简化为图2，其振动微分方程为：

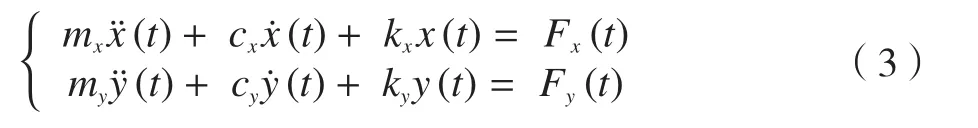
式中：mi、ci、ki（i=x，y）分别表示系统在x、y方向上的质量、阻尼和刚度，x（t）、y（t）表示刀齿在x、y方向上的动态位移，Fx（t）、Fy（t）则表示系统在x、y方向上的分力。

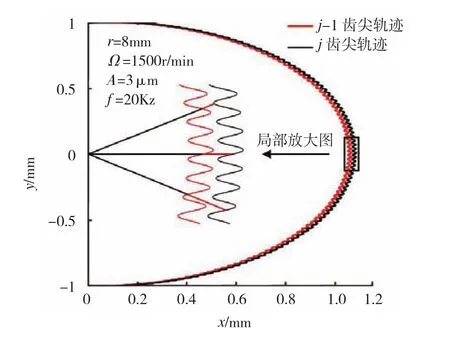
图1 相邻齿尖运动轨迹仿真图Fig.1 Trajectory simulation of adjacent tool nose

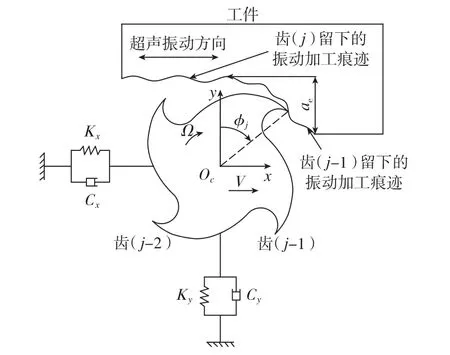
图2 不分离型超声铣削动力学模型Fig.2 Dynamic model of unseparated ultrasonic combined milling

综合考虑刀具进给方向和垂直刀具进给方向（y方向）的振动，采用指数型切削力模型的第j刀齿的切削力可表示为:

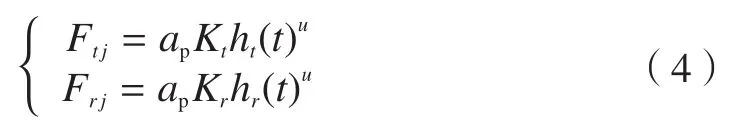
式中，ap是轴向切削深度，Kt和Kr分别是切向和切削力系数，u为切削常数，hj（t）是瞬时切削厚度。

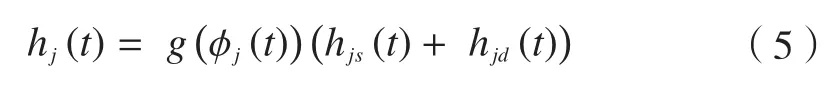
式中，刀齿切削状态下g（φj）等于1，不切削状态等于0；φj是刀齿j的转动角度；瞬时切削厚度有hjs（t）和hjd（t）两部分组成，hjs（t）是刀具进给量和在超声振动刀具进给方向上共同作用下的静态切厚，hjd（t）则是相邻两刀齿由于加工过程中再生效应引起的动态切削厚度。

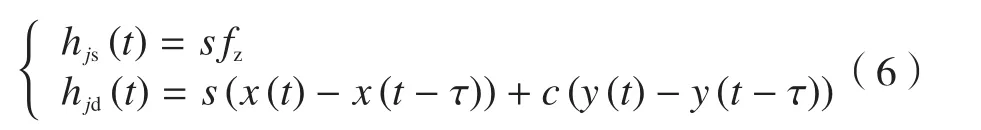
式中，s=sin（φj（t）），c=cos（φj（t））；

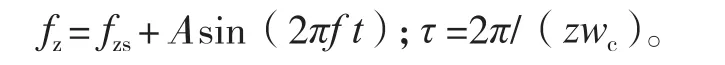
根据文献[13-14]将非线性周期函数用线性函数代替的方法，将式（4）、式（5）、式（6）代入式（3），不分离型超声复合铣削动力学方程可简化表示为：

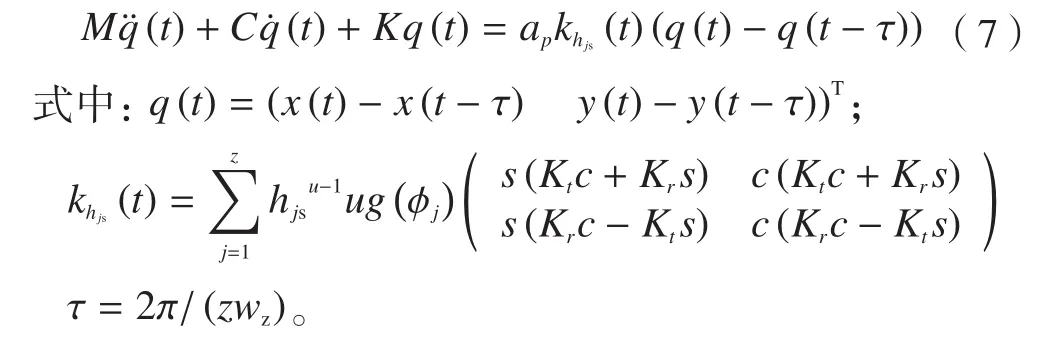
在高速铣削稳定性研究方面，无论采用半离散法[5]、全离散法[6]还是时间有限元法[1]等都是在没有附加超声振动的情况下进行的，考虑到半离散法的特点和适用性，研究不分离型超声振动铣削系统的稳定性，在此引入半离散法。

根据文献[5]，对式（7）进行Cauchy变换可得：

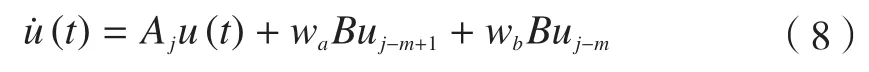
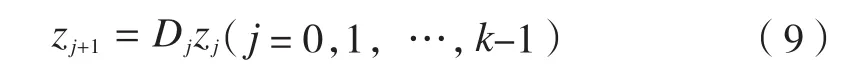
在时间周期T=kΔt上有转移矩阵：

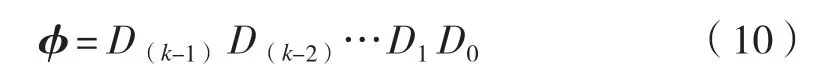
根据Floquet原理，要使超声复合铣削系统稳定，则必须方程（10）的特征值的模小于1，由此可以得到超声复合铣削下，主轴转速与轴向切削深度构成的超声复合铣削稳定性叶瓣图。

3 超声铣削系统稳定性仿真分析及试验验证

3.1 稳定性预测

超声复合铣削系统的仿真参数见表1，表1中的切削力系数由试验获得，Z为铣刀齿数，且模态参数[13]分别为:

为方便起见，将超声振动复合铣削和普通铣削的预测图置于同一图中。由式（8）～（10），通过仿真可以获得超声复合铣削预测图，通过稳定性模型[5]给出了普通铣削的预测图，如图3所示。

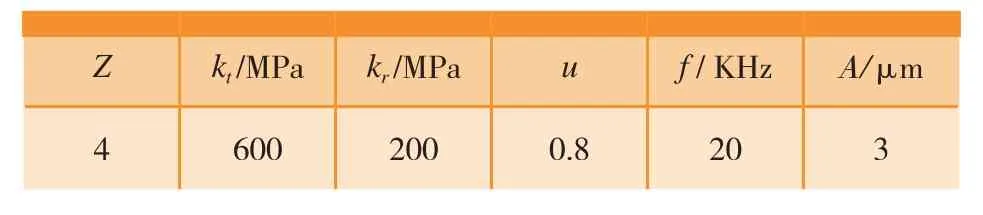
表1 铣削系统仿真参数

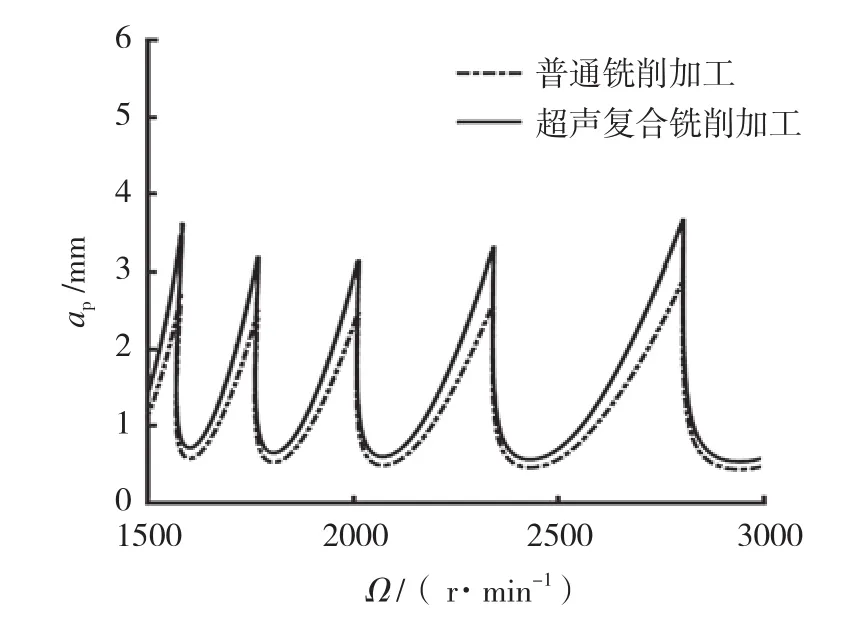
图3 铣削稳定性预测图Fig.3 Milling stability prediction map

图3 表明，与普通铣削相比，不分离型超声复合铣削系统不仅可以提高铣削系统切削深度的极限值（比普通铣削极限深度最大提高约13.8%），也能够增大稳定性的区域。这是因为在铣削过程中，由于工件的高频振动（振动频率远大于主轴转速），破环了前后刀齿留下的加工振纹，减少了自激振动发生的几率。另外，刀尖与工件呈现不分离切削状态，但是由于超声高频振动的存在，刀尖在工件上的往复运动，使切削液更容易渗透到加工区域，从而改善了切屑与刀具的摩擦，也有利于降低切削温度。

3.2 试验验证

图4 加工装置Fig.4 Machining devices

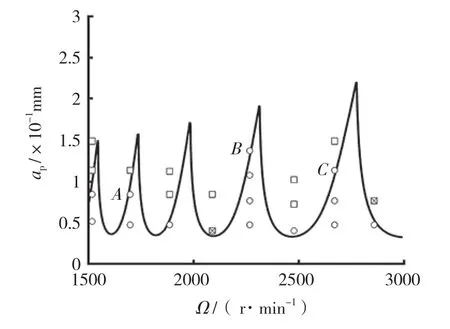
图5 铣削稳定性预测图及试验验证参数点Fig.5 Milling stability prediction diagram and experimental verification parameters

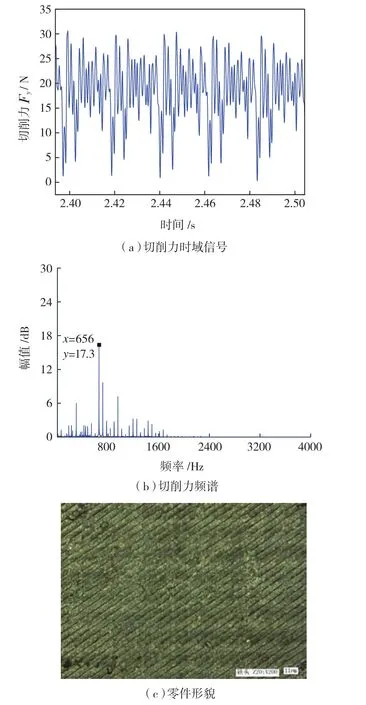
图6 B点普通铣削Fig.6 Traditional milling of B point

为了验证不分离型超声复合铣削稳定域叶瓣图的准确性，在数控加工中心VMC850E进行了试验验证，如图4所示。

试验所采用仪器有kistler 9257B测力仪，基恩士VHX-2000型超景深显微镜等。刀具直径为φ6mm，螺旋角为30°。工件材料选用Ti6A14V，尺寸大小为30mm×10mm×15mm。超声加工装置自行研制，超声复合铣削的声学参数：A=3μm，f=19.65KHz，径向切深ae=1mm。超声复合系统的模态参数由文献[15]方法得到，切削力系数由正交回归试验获得：kt= 9.38×108MPa，kr=4.65×108MPa。

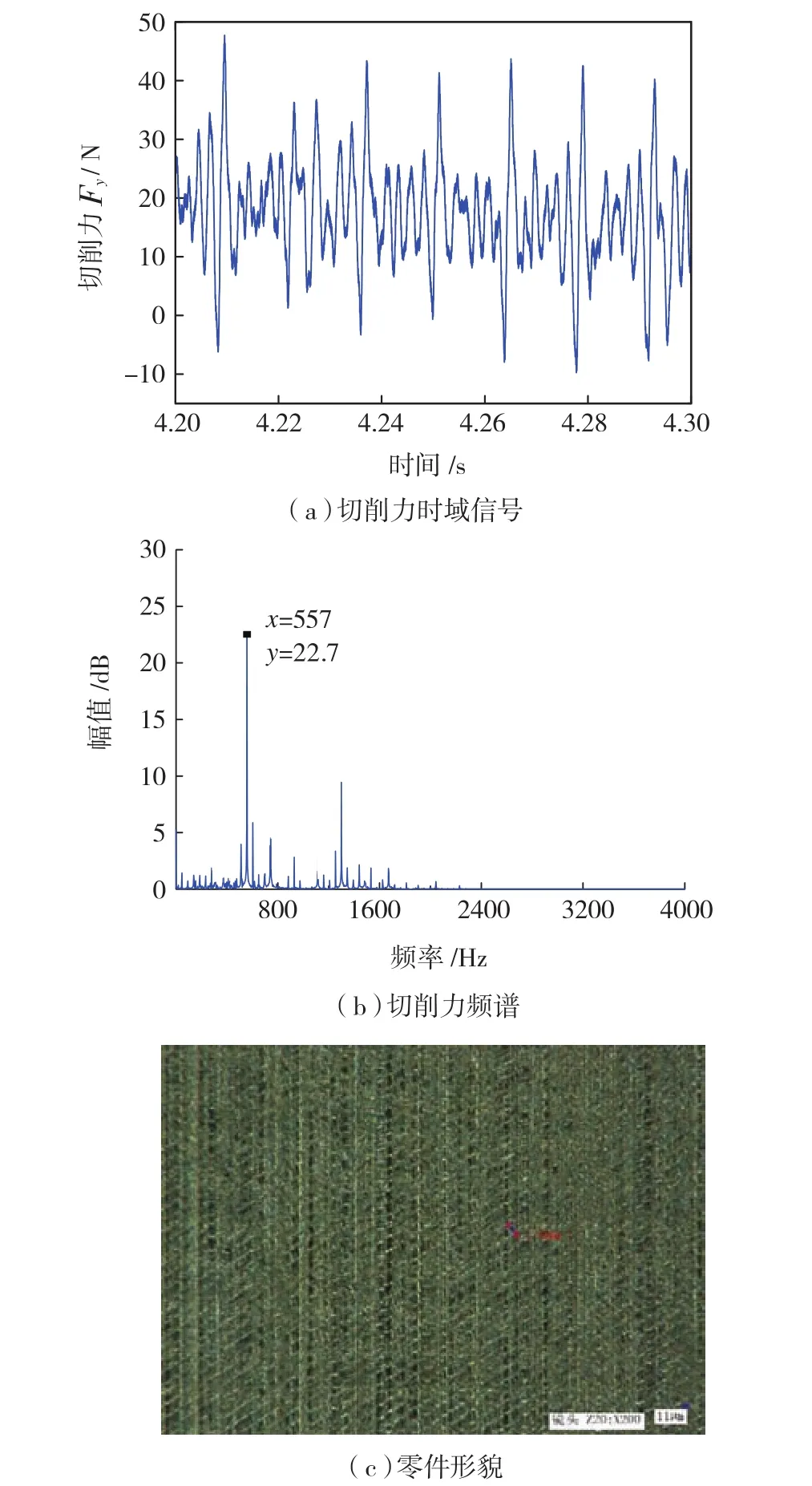
图7 B点超声铣削Fig.7 Ultrasonic milling of B point

根据本文所建立的不分离型超声复合铣削稳定性模型，图5给出了上述加工条件下铣削稳定性叶瓣图。图5中“○”、“□”和“◇”等分别表示系统稳定点、颤振点和无法判断铣削稳定性的点，图5中B和C点表示在普通铣削中为不稳定铣削点，而在不分离型超声复合铣削则变成稳定铣削，A点则转化为临界点。

为了比较径向超声振动复合铣削与普通铣削的区别，从图5中选择B点（2250r/min，0.15mm）进行研究，在普通铣削和超声复合铣削条件下的X向切削力时域信号，频谱图以及加工后的零件形貌如图6和图7所示。

从图6和图7中可以看到，普通铣削下的切削力和不分离型超声复合铣削下的切削平均力大小基本相等，但是从频谱图中可以明显看出不分离型超声复合铣削下的谐波分量明显被抑制，提高铣削系统的稳定性，验证了本文所提出的不分离型超声复合铣削稳定性模型的正确性。

4 结论

（1）讨论了不分离超声复合铣削运动特性，建立了超声复合铣削稳定性模型，应用MATLAB软件进行数值分析方法得到了超声铣削稳定性叶瓣图。

（2）运用半离散法的不分离型超声复合铣削系统能合理选择出切削稳定性极限区域，并且能够提高铣削系统的稳定性，最大提高约13.8%。

（3）本试验是在数控加工中心VMC850E完成的，验证了不分离型超声复合铣削稳定性模型以及稳定性叶瓣图的正确性，说明了应用半离散法分析超声复合铣削系统定性是可行的。

[1]姜燕，郭强，赵波. 铣削稳定性预测的时间有限元法[J].河南理工大学学报（自然科学版），2016，35(5)： 672-676.JIANG Yan，GUO Qiang，ZHAO Bo. The method on the stability limit prediction for milling process based on time-finite-element theory[J].Journal of Henan Polytechnic University (Natural Science), 2016,35(5):672-676.

[2]唐军，赵波. 分离型纵-扭复合超声铣削的稳定性分析[J].兵工学报，2015，36(7):1318-1325.TANG Jun, ZHAO Bo. Stability analysis of the separated longitudinaltorsional composite ultrasonic milling[J]. Acta Armamentarii, 2015, 36(7):1318-1325.

[3]ALTINTAS Y. 数控技术与制造自动化[M]. 罗学科，译. 北京:化学工业出版社，2002:76-85.ALTINTAS Y. Manufacturing automation: metal cutting mechanics,machine tool vibrations, and CNC design [M]. LUO Xueke，tran. Beijing:Chemical Industry Press，2002:76-85.

[4]MERDOL S D, ALTINTAS Y. Multi frequency solution of chatter stability for low immersion milling[J]. Science and Engineering，2004，126(3)：459-466.

[5]INSPERGEN T, STÉPÁN G. Updated semi-discretization method for periodic delay-differential equation with discrete delay[J]. International Journal for Numerical Methods in Engineering,2004,61: 117-141.

[6]DING Y, ZHU L M, ZHANG X J , et al. A full-discretization method for prediction of milling stability[J]. International Journal of Machine Tools & Manufacture, 2010,50: 502-509.

[7]于劲，周小勤. 基于高频变速特征的不分离型超声波振动车削抑制颤振机理[J]. 兵工学报，1993，14 (1): 52-57.YU Jin，ZHOU Xiaoqin. On the mechanism of chatter suppression with high frequency and vari-speed unseparated type ultrasonic vibration turning[J]. Acta Armamentarii，1993，14(1) : 52-57.

[8]方成刚. 数控强力切削的颤振机理研究[D].南京: 南京工业大学,2004.FANG Chenggang. Study on the mechanism of chatter in CNC heavy cutting[D]. Nanjing: Nanjing University of Technology,2004.

[9]YANG F，ZHANG B，YU J. Chatter suppression via an oscillating cutter[J].Journal of Manufacturing Science and Engineering，Transactions of the ASME，1999，121(1) : 54-60.

[10]MEI C. Active regenerative chatter suppression during boring manufacturing proc[J]. Robotics and Computer-Integrated Manufacturing，2005，21(2) : 153-158.

[11]皮均，徐希鹏. 纵扭共振超声铣削研究[J]. 中国机械工程，2009，20(10):1163-1169.PI Jun, XU Xipeng. Research on Longitudinal-torsional resonance ultrasonic milling(LTRUM)[J]. China Mechanical Engineering,2009,20(10):1163-1168.

[12]张建华. 超声振动辅助微细铣削运动学分[EB/OL].(2012-12-28)[2016-09-10]. http://www.paper.edu.cn/releasepaper/content/201212-1173.ZHANG Jianhua. Ultrasonic vibration assisted micro milling[EB/OL]. (2012-12-28)/[2016-09-10]. http://www.paper.edu.cn/releasepaper/content/201212-1173.

[13]FAASSEN R P H, VAN DE WOUWN, OOSTERLING J A J,et al. Prediction of regenerative chatter by modelingand analysis of highspeed milling[J]. International Journal of Machine Tools & Manufacture,2003, 43:1437-1446.

[14]宋清华，艾兴，万熠,等. 小径向切深下的进给量对铣削稳定性的影响[J].中国机械工程，2008，19(10)，1148-1152.SONG Qinghua, AI Xing, WAN Yi, et al. Stability prediction for high-speed milling including feed rate in low radial immersion [J]. Chinese Journal of Mechanical Engineering, 2008, 19(10): 1148-1152.

[15]李德葆，陆秋海.实验模态分析及其应用[M]. 北京：科学出版社，2001.LI Debao, LU Qiuhai. Experimental modal analysis and application[M]. Beijing: Science Press, 2001.