改进遗传算法的CSAMT一维反演
孙彩堂,李玲,王雪,黄维宁,周逢道
(国家地球物理探测仪器工程技术研究中心(吉林大学),吉林大学 仪器科学与电气工程学院,吉林 长春 130061 )
改进遗传算法的CSAMT一维反演
孙彩堂,李玲,王雪,黄维宁,周逢道†
(国家地球物理探测仪器工程技术研究中心(吉林大学),吉林大学 仪器科学与电气工程学院,吉林 长春 130061 )
传统的可控源音频大地电磁法(CSAMT)反演方法属于线性或者局部线性,大都依赖初始模型.而遗传算法因其不依赖初始模型的特点而应用到CSAMT反演中.但是,标准的遗传算法存在早熟、局部收敛等问题.针对这些问题,对标准的遗传算法进行改进,采用排序法和最优保留策略相结合的选择算子,增强其种群多样性并保证其收敛性;采用父子竞争策略和自适应概率法相结合的交叉算子,能够防止好的父代个体被淘汰,又具有适应性.通过理论模型进行算法仿真验证,证明其有效性,说明改进遗传算法较标准遗传算法在CSAMT一维反演中有明显的改善.通过对实测数据进行反演,其结果与地质资料吻合,证明了其适应性.
可控源音频大地电磁;反演;改进遗传算法
在地球物理勘探方法中,可控源音频大地电磁法[1-3](CSAMT)是一种重要的方法.反演[4-7]是CSAMT方法的关键环节之一.经典的线性或者局部线性反演方法大都依赖初始模型,或者出现病态矩阵使得反演失败.遗传算法[8-12](GA)因其不依赖初始模型等优点而被广泛应用.但是,标准的遗传算法可能存在早熟和局部收敛等问题.因此,对标准的遗传算法进行优化是必要的.刘云峰等[13]引进了“小生境”GA法对一维大地电磁测深地电模型进行处理,并对目标函数进行压缩,有利于目标函数相近时选择,计算复杂地电模型十分有效.Elsayed S M等[14]提出了求解最优化问题的一种新的遗传算法.Fernandes D R M[15]等提出了对于二阶容量选址的简单有效的遗传算法.其他学者对遗传算法的优化方法[16-17]就不再详细列举.本文采用改进遗传算法,对于选择算子采用排序法和最优保留策略相结合的选择算子,对于交叉算子采用父子竞争策略和自适应概率法相结合的交叉算子.改进的算法有效地克服了标准遗传算法存在的问题.
1 正演计算
本文研究可控源音频大地电磁法的一维反演,反演的前提是正演.假设地电模型是均匀水平层状的,其示意图如图1所示.
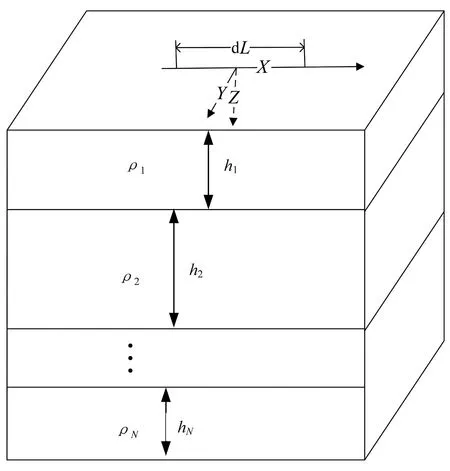
图1 均匀水平层状地下介质模型示意图
图1中标明了每层的厚度hi和每层的电阻率ρi,dL是电偶极源长度.
通过理论计算知卡尼亚视电阻率公式如下:
(1)
式中:Ex指的是电场的水平分量;Hy是磁场的水平分量;μ是空气中的磁导率;ω是角频率.
视相位公式如下:
φ=φE-φH
(2)
式中:φE和φH分别是观测点上电场和磁场的相位.
2 标准遗传算法
遗传算法满足“适者生存、优胜劣汰”的原则.其基本步骤是根据实际问题确定参数及编码方式,形成初始种群;进行遗传操作,包括选择、交叉、变异操作;多次迭代,输出结果.
标准遗传算法[18-19]中,选择采用轮盘赌的方式;交叉采用基本的交叉方式(单点交叉);变异采用基本的变异方式.
对于CSAMT一维反演而言,根据具体问题可以确定参数为每层的电阻率和厚度.因此,可确定目标函数,它是模型值与观测值之间的相对误差,其公式如下:
E(m)=
(3)
式中:E(m)表示染色体m的目标函数;N是发射的频点数;ρri(m)和φri(m)分别表示第i个频率下观测的视电阻率和视相位;ρoi和φoi分别表示在第i个频率下模型的视电阻率和视相位.
适应度函数判断再生概率大小,其公式如下:
(4)

3 改进遗传算法
针对标准遗传算法存在的问题,本文对标准遗传算法进行改进,其流程图如图2所示.

图2 改进遗传算法的基本流程图
3.1 目标函数和适应度函数
目标函数采用标准遗传算法时的式(3),用其来进行遗传操作.
适应度函数则根据本文改进方法的特点,确定其公式如下:
f(m)=e-E(m)
(5)
其中f(m)表示染色体m的适应度函数;E(m)为染色体m的目标函数,该函数将目标函数归一化,同时将目标函数最小化问题转换为适应度函数最大化问题.
3.2 改进的选择算子
选择算子采用基于适应度值的排序法和最优个体保留法相结合的选择方法.
排序法:将计算得到的目标函数值,按照从小到大的顺序进行排序,并平均分成4份,把第1个1/4复制两份,第2个1/4复制一份,最后一份随机生成.
最优个体保留策略:当前群体中适应度值最大的个体替换本代群体中经过交叉、变异后所产生的适应度值最小的个体.
改进的选择算子既能保证算法收敛,也有利于保持种群的多样性.
3.3 改进的交叉算子
交叉算子采用父子竞争策略和自适应概率法相结合的交叉算子.
自适应概率法.分段的交叉概率上下限,对交叉概率的上下限进行设定,假定最大的迭代次数为M,交叉概率的上限是pc1,交叉概率的下限是pc2,设置如下:
第1阶段范围是[0,0.3M],pc1=0.8,pc2=0.6;
第2阶段范围是[0.3M, 0.6M],pc1=0.7,pc2=0.5;
第3阶段范围是[0.6M,M],pc1=0.6,pc2=0.3.
其自适应交叉概率公式为:

(6)
式中,pc1和pc2分别是交叉概率的上下限;fi为第i个染色体的适应度值;favg为当代种群所有个体的平均适应度值;fmax为当代种群中最大适应度值.
父子竞争策略.交叉前后的染色体比较其适应度值的大小,保留适应度值较大的两个个体.
改进的交叉算子既能防止父代好的个体被淘汰,又具有自适应调节的功能.
4 模型仿真分析
本文用2层地电模型G和2层地电模型D和3层地电模型A和3层地电模型H分别进行标准遗传算法(Standard genetic algorithm,简称SGA)的CSAMT一维反演和改进遗传算法(Improved genetic algorithm,简称IGA)的CSAMT一维反演,对比分析改进算法的性能,得出结论.在实验中,对每个参数给出具体模型值,搜索范围,以及每个参数的二进制位数即染色体的长度,然后进行计算仿真.
4.1 2层地电断面反演
对G型断面模型分别进行SGA和IGA的6次实验,其实验结果如表1和表2所示,其中包括标准遗传算法CSAMT一维反演结果和改进遗传算法的CSAMT一维反演结果.由表1可知,标准遗传算法下的反演结果会陷入局部极值的状况,出现与模型值存在较大差距的情况.
由表2可知,改进遗传算法下的反演结果与模型值相近,6次实验结果波动较小.
通过表1和表2可以得到标准遗传算法的误差率结果和改进遗传算法的误差率结果,其结果如表3和表4所示.

表1 G型断面模型SGA反演结果

表2 G型断面模型IGA反演结果

表3 G型断面模型SGA误差率

表4 G型断面模型IGA误差率
由表3可知,6次实验的单次误差率在10%左右,实验3出现了较大误差达到21.2%,可能出现局部收敛现象,SGA平均误差率是9.8%.
由表4可知,6次实验单次均差率也在3%以内,各个参数的6次实验的平均误差率也在2%左右,6次实验平均误差率是1.9%.
通过比较可知,改进遗传算法得到的CSAMT一维反演结果的误差率比标准遗传算法得到的CSAMT一维反演误差率减少了8%左右,有较好的改善效果.
对D型断面模型分别进行SGA和IGA的6次实验,其结果如表5和表6所示.

表5 D型断面SGA反演结果
由表5知,实验3出现了早熟现象,与模型相差较大,通过计算得到6次实验平均误差率是17.1%.
由表6知,6次实验与模型值相差不大,通过计算可得到6次实验平均误差率是1.5%.改进遗传算法的CSAMT一维反演的误差率比标准遗传算法误差率降低了16%左右.
4.2 三层地电断面反演
三层地电断面包括A型和Q型,对其分别进行标准遗传算法和改进遗传算法的CSAMT一维反演.A型断面反演结果如表7所示,H型断面反演结果如表8所示.

表7 A型断面结果
通过表7可知,A型断面标准遗传算法的反演结果与模型相差较大,可能出现了局部极值的情况,SGA 反演的平均误差率是36.4%.改进遗传算法的反演结果与模型相差较小,IGA反演平均误差是7.1%,比标准遗传算法的平均误差率小了近29%,证明了本文改进算法的有效性.但是,h2的误差率达到了26.8%,没有其他参数的反演效果好,可能是h2陷入了局部极值,导致误差增大.
图3和图4分别是A型曲线的SGA和IGA的反演结果图,由图3和图4可知,对于A型断面模型来说,SGA反演曲线和模型曲线会出现较大的波动,拟合不是很好.IGA反演曲线和模型取线拟合较好,证明IGA的改进性.
由表8可知,Q型断面标准遗传算法的反演结果与模型相差较大, SGA 反演的平均误差率是23.2%.改进遗传算法的反演结果与模型接近,IGA反演平均误差是6.3%,比标准遗传算法的平均误差率小了16%左右,证明了本文改进算法的有效性.

表8 Q型断面反演结果
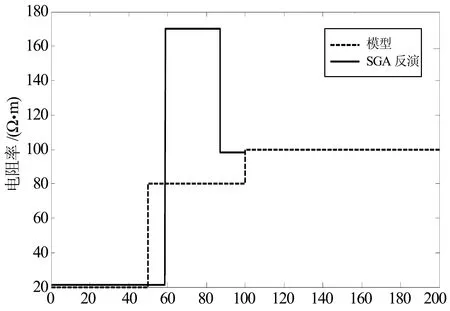
深度/m

深度/m
5 实测数据反演
采用本文方法对黑龙江东京城的地热勘查数据进行了反演解释.
根据东京城镇区域地质资料,了解到工作区域剖面解释大致为3层,表层为第4系或强烈风化的砂岩,电阻率值较小.第2层电阻率值较高,为白垩系的砂岩、粉砂岩.第3层电阻率很高,总体在几千至一万欧姆米左右,为致密的花岗岩.本文选择了一条全长2.4 km的测线.供电偶极距AB约为1.4 km,收发距r=10 km.用本文的方法对测线的整个剖面进行反演,反演结果如图5所示.
由图5可知,表层电阻率较低,为30 Ω·m左右;随着地层厚度的增加,电阻率变为100 Ω·m左右;剖面自上而下,电阻率逐渐增加,到剖面的底部反演电阻率值达到10 000 Ω·m.
因此,可知反演结果和地质资料吻合,说明该方法可用于实测野外资料的处理.

点号
6 结 论
对标准遗传算法进行改进,并应用到CSAMT的一维反演,通过具体的2层和3层地电模型的实例仿真,验证了改进遗传算法效果.通过实测数据反演,验证改进遗传算法的适应性.本文研究得出以下几个方面的结论:
首先,选择算子采用排序法和最优个体保留法相结合的选择方法,其中排序法可以保证每一代种群的多样性,避免陷入局部极值的状况;而最优个体保留法又保证了算法的收敛性.
其次,交叉算子采用父子竞争策略和自适应概率法相结合的交叉方法,其中父子竞争策略可避免父代优良个体被淘汰,而自适应概率法则可根据种群的实际情况自适应调节交叉概率,更具适应性.
最后,通过具体模型和实测数据的仿真,可以得出改进遗传算法比标准遗传算法更具优越性,可以克服标准遗传算法存在的问题,并在CSAMT一维反演中得以应用,取得有效的反演结果.
[1] FU C, DI Q, AN Z. Application of the CSAMT method to groundwater exploration in a metropolitan environment[J]. Geophysics, 2013, 78(5): B201-B209.
[2] 张健. 可控源音频大地电磁法一维正反演研究[D].成都:成都理工大学信息工程学院, 2011.
ZHANG Jian. The study of simulation and inversion of 1D controlled source audio-frequenc magnetotellurics method[D].Chengdu:Department of Information and Engineering,Chengdu University of Technology,2011.(In Chinese)
[3] 雷达. 起伏地形下CSAMT二维正反演研究与应用[J]. 地球物理学报, 2010, 53(4): 982-993.
LEI Da. Studies and applications of 2-D CSAMT modeling and inversion with a dipole source and topography[J]. Chinese Journal of Geophysics, 2010, 53(4): 982-993. (In Chinese)
[4] 王若, 王妙月. 一维全资料 CSAMT 反演[J]. 石油地球物理勘探, 2007, 42(1): 107-114.
WANG Ruo, WANG Miaoyue. CSAMT inversion of one-dimensional data[J].Oil Geophysical Prospecting, 2007, 42(1): 107-114. (In Chinese)
[5] 赵忠, 谭玉阳, 张洪亮, 等. 基于 Occam 反演算法的微地震速度模型反演[J]. 北京大学学报: 自然科学版, 2015,51 (1): 43-49.
ZHAO Zhong, TAN Yuyang, ZHANG Hongliang,etal. Velocity model inversion for microseismic monitoring based on Occam inversion algorithm[J].Acta Scientiarum Naturalium Universitatis Pekinensis, 2015,51 (1): 43-49. (In Chinese)
[6] 周东霞.几种反演方法在CSAMT资料处理中的应用[J].企业技术开发,2011,30(3):96-99.
ZHOU Dongxia. Application of several inversion method in CSAMT material processing[J].Technological Development of Enterprise, 2011,30(3):96-99. (In Chinese)
[7] WANG R, YIN C, WANG M,etal. Laterally constrained inversion for CSAMT data interpretation[J]. Journal of Applied Geophysics, 2015, 121: 63-70.
[8] KOSTENKO V A, FROLOV A V. Self-learning genetic algorithm[J]. Journal of Computer and Systems Sciences International, 2015, 54(4): 525-539.
[9] 王光杰,王勇,李帝铨,等.基于遗传算法CSAMT反演计算研究[J].地球物理学进展,2006,21(4):1285-1289.
WANG Guangjie, WANG Yong, LI Dikui,etal. The application of genetic algorithm to CSAMT inversion[J].Progress in Geophysics, 2006,21(4):1285-1289. (In Chinese)
[10]AKDEMIR D, SANCHEZ J I, JANNINK J L. Optimization of genomic selection training populations with a genetic algorithm[J]. Genet Sel Evol, 2015,47(1):38.
[11]JIANG D, FAN Z. The algorithm for algorithms: an evolutionary algorithm based on automatic designing of genetic operators[J]. Mathematical Problems in Engineering, 2015.
[12]马永杰, 云文霞. 遗传算法研究进展[J]. 计算机应用研究, 2012, 29(4): 1201-1206.
MA Yongjie, YUN Wenxia. Research progress of genetic algorithm[J]. Application Research of Computers, 2012, 29(4): 1201-1206. (In Chinese)
[13]刘云峰, 曹春蕾. 一维大地电磁测深的遗传算法反演[J]. 浙江大学学报:自然科学版, 1997, 31(3): 300-305.
LIU Yunfeng CAO Chunlei. One dimensional genetic algorithm inversion of magnetotelluric sounding[J].Journal of Zhejiang University:Natural Science, 1997, 31(3): 300-305. (In Chinese)
[14]ELSAYED S M, SARKER R A, ESSAM D L. A new genetic algorithm for solving optimization problems[J]. Engineering Applications of Artificial Intelligence, 2014, 27: 57-69.
[15]FERNANDES D R M, ROCHA C, ALOISE D,etal. A simple and effective genetic algorithm for the two-stage capacitatedacility location problem [J]. Computers & Industrial Engineering, 2014, 75: 200-208.
[16]曹凯,陈国虎,江桦,等. 自适应引导进化遗传算法[J]. 电子与信息学报, 2014, 36(8): 1884- 1890.
CAO Kai, CHEN Guohu, JIANG Hua,etal. Guided self-adaptive evolutionary genetic algorithm[J]. Journal of Electronics & Information Technology, 2014, 36(8): 1884- 1890. (In Chinese)
[17]邢小宁, 井西利, 马毅恒, 等. 自适应混合遗传算法优化团簇[J]. 计算物理, 2012, 29(3): 459-465.
XING Xiaoning, JING Xili, MA Yiheng,etal. Adaptive hybrid genetic algorithm for atomic clusters[J].Chinese Journal of Computational Physics, 2012, 29(3): 459-465. (In Chinese)
[18]曾文飞, 张英杰, 颜玲. 遗传算法的基本原理及其应用研究[J]. 软件导刊, 2009,8(9):54-56.
ZENG Wenfei, ZHANG Yingjie, YAN Ling. The basic principle of genetic algorithm and its application [J]. Software Guide, 2009,8(9):54-56. (In Chinese)
[19]孙树栋, 周明. 遗传算法原理及应用[M].北京:国防工业出版社, 1999:27-35.
SUN Shudong, ZHOU Ming. Theory and application of genetic algorithms [M]. Beijing: National Defence Industry Press, 1999:27-35. (In Chinese)
CSAMT One-dimensional Inversion Based on Modified Genetic Algorithm
SUN Caitang, LI Ling, WANG Xue, HUANG Weining, ZHOU Fengdao†
(National Geophysical Exploration Engineering Research Center (Jilin University), College of Instrumentation and Electrical Engineering, Jilin University, Changchun 130061, China)
The traditional method of controlled source audio frequency magnetotelluric (CSAMT) inversion is linear or locally linear, and most of them depend on the initial model. The genetic algorithm is applied to the CSAMT inversion because it does not depend on the initial model. However, the standard genetic algorithm has some problems such as premature convergence and local convergence. The standard genetic algorithm was improved, and the selection operator based on the ranking method and the optimal reservation strategy was used to enhance the diversity of the population and to ensure its convergence; The crossover operator, which is based on the combination of the father and son competition strategy and the adaptive probability method, can prevent the good parent from being eliminated, and has the adaptability. The simulation results show that the improved genetic algorithm is better than the standard genetic algorithm in the one-dimensional inversion of CSAMT. The inversion of the measured data is consistent with the geological data, which proves the adaptability of the improved genetic algorithm.
controlled source audio-frequency magnetotellurics (CSAMT); inversion; modified genetic algorithm
1674-2974(2017)04-0102-07
10.16339/j.cnki.hdxbzkb.2017.04.014
2016-06-26
吉林省科技厅发展计划重点项目(20100349),The Key Projects of Sciemce and Technology Development Plan of Jilin Province(20100349);国家潜在油气资源产学研用合作创新研究项目(OSR-02),National Potential Oil and Gas Resources with Cooperation Innovation Projects of Production(OSR-02)
孙彩堂(1975-),男,吉林长春人,吉林大学副教授,博士†通讯联系人,E-mail:zhoufd@jlu.edu.cn
P631.2
A

