基于免组装有限元的悬架控制臂拓扑优化
卞翔,方宗德
(西北工业大学 机电学院,陕西 西安 710072)
基于免组装有限元的悬架控制臂拓扑优化
卞翔†,方宗德
(西北工业大学 机电学院,陕西 西安 710072)
为了提高拓扑优化在实际工程应用中的速度,将一种基于拓扑灵敏度的拓扑优化算法与免组装有限元法结合,对汽车悬架控制臂进行多工况拓扑优化.该方法使用一致的体素单元划分网格,用压缩共轭梯度法(DCG)加速有限元的求解,得到结构的应力和应变场,从而获得拓扑灵敏度场,用来控制结构拓扑变化.通过添加多工况优化以及加工约束功能,使该方法更符合工程应用的要求.通过对比,该方法和商用软件能够获得性能接近、形状相似的优化结构,而整个优化过程的速度有显著提高.
悬架控制臂;多工况拓扑优化;免组装有限元;体素化;压缩共轭梯度法;拓扑灵敏度
轻量化设计是汽车设计中的一项重要内容,对于降低重量、提高性能、降低油耗等有重要作用.拓扑优化技术在汽车结构的轻量化设计中运用越来越多,拓扑优化能在结构设计的初始阶段提供一个概念性设计,使结构在布局上采用最优方案,改变了以往的设计、校核、修改这样一个不断反复的开发流程,可以提高设计效率和质量,缩短研发周期,降低成本.
近年来,拓扑优化技术逐渐成熟,国内外研究较多的有固体各向同性材料惩罚法(Solid Isotropic Material with Penalization,SIMP)[1],进化结构优化法(Evolutionary Structural Optimization,ESO)[2-3],水平集法(Level-Set)[4-5]等.其中SIMP方法基于有限元法,给每个单元赋予伪密度,通过优化各单元的伪密度来达到优化目标[6].由于其概念简单,算法容易实现,被推广应用于多材料、多工况、多物理场等多种实际问题中,成为主流的拓扑优化方法之一[7].目前,常用的商用拓扑优化软件如 Hyperworks 和 ANSYS 都采用SIMP方法进行拓扑优化.国内有许多研究使用Hyperworks进行汽车零部件的拓扑优化设计,文献[8-11]使用Hyperworks对转向节、悬架控制臂、发动机悬置支架、车架等汽车结构进行了拓扑优化设计.
如今,拓扑优化技术发展的挑战之一是计算速度[12],尤其是对于大型有限元模型,比如对于上百万自由度的优化问题需要数小时甚至数天来完成.文献[12-14]提出了一种基于拓扑灵敏度的拓扑优化算法,对多目标优化问题帕雷托最优解的计算十分高效,该方法将拓扑灵敏度作为水平集,用来控制孔洞的形成,得到的结果相比于SIMP方法更加清晰、明确,不需要网格过滤等技术.但是这种方法的研究还处于初步阶段,没有商用软件全面的功能,还不能满足实际的工程应用.
本文基于C++语言,将这种基于拓扑灵敏度的拓扑优化算法与一种免组装(Assembly-free)有限元分析方法[15-16]相结合,并用压缩共轭梯度法[17]进一步加速拓扑优化的速度,通过添加多工况优化、加工约束等满足实际工程应用的功能,用于汽车零部件的结构优化设计.以悬架控制臂的优化为例,通过与商用软件Hyperworks对比,证明该方法的有效性.
1 免组装有限元模型
1.1 悬架控制臂体素化模型
一些商用软件需要花费大量时间在网格划分上,需要人工进行简化几何、拆解几何和改变网格尺寸等操作,才能获得满足软件要求的网格模型.
体素化[18]是一种简单的有限元网格离散方法,通过统一的六面体单元(体素)来划分几何模型.由于使用了形状和尺寸一样的单元,体素化网格具有稳健性和内存占用空间低的优点[19],能够配合免组装方法,提高有限元分析的计算速度.
体素化模型由于使用一致的网格,可以通过编程实现快速的自动网格划分,图 1 (a)所示是悬架控制臂的几何模型,图1(b)为相应的体素网格模型,单元数量为79 000,自由度为280 000,自动网格划分时间仅为4 s.
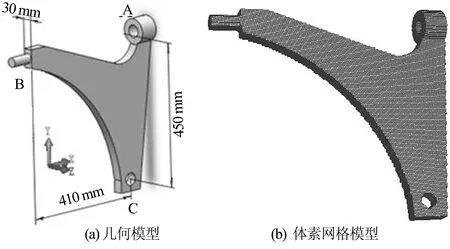
图1 悬架控制臂体素化网格
由于网格一致性的限制,体素化模型不能够完全精确体现所有的几何细节.但是考虑到拓扑优化是设计初期的概念设计阶段,其主要目的是为后期设计提供参考,在多数情况下,尤其是对于诸如柔度、频率等全局参数的优化变量,一些几何细节并不重要.对于本文考虑的悬架控制臂模型,3个连接端这几个细节部分都属非设计区域,细节的计算精度并不影响主体设计区域的拓扑优化,所以体素化网格适用于本文对悬架控制臂的拓扑优化.
1.2 免组装的压缩共轭梯度法
拓扑优化中的迭代过程需要进行多次有限元求解,本文将基于压缩共轭梯度法的免组装有限元算法引入到拓扑优化过程中,可以提高每次有限元分析的速度,从而大幅缩短整个拓扑优化过程的时间.
免组装(Assembly-free)有限元法,即总刚矩阵免组装的有限元法,最初是Hughes等[15]在1983年提出的,随着并行算法的发展,这种方法也得到了改进[17].免组装有限元方法的基本概念是单元刚度矩阵不用组装成总体刚度矩阵,而是在单元层面进行稀疏矩阵向量乘法.换而言之是将“组装然后相乘”的过程:
(1)
变为“相乘然后组装”:
(2)
式中:K为总体刚度矩阵;d为位移向量.
共轭梯度法ConjugateGradient(CG)是求解大型稀疏线性方程的一种迭代算法,迭代过程中最占用计算时间的是矩阵向量乘法运算Kd,其大部分的内存占用来自存储和提取刚度矩阵.如上节所述,由于结构使用统一的单元进行网格划化,所有单元的形状和尺寸是一样的,所以单元刚度矩阵是一样的,不需要组装并存储总体刚度矩阵K,而只需要储存单个单元刚度矩阵Ke.这将大大减少内存占用,提高矩阵向量乘法运算的速度,从而提高迭代算法的计算速度.
压缩共轭梯度法Deflated Conjugate Gradient (DCG)是一种加速的迭代算法[20].它将有限元网格的点划分成少数的几块,把每块网格当作刚体处理,构造出压缩空间.在某块里的一个点的位移表示为
(3)
式中:(u0,v0,w0,θx,θy,θz)T是此块在6个自由度上的刚体运动.(x,y,z)是该块中一点相对此块几何中心的坐标.通过所有点的相对坐标,构造出压缩矩阵W,于是有:
d=Wλ
(4)
式中:d有3N个自由度(N是所有点个数);λ是6G个与块相关的自由度(G是分块的个数).可以使用压缩空间矩阵W进行共轭梯度运算.(具体推导及理论分析可参考文献[21]).由于分块的数量G远小于节点数量N,所以压缩矩阵的尺度比刚度矩阵的小,在迭代过程中能够提高矩阵向量乘法运算的速度,从而对迭代过程起到加速作用.同时,这种压缩共轭梯度算法也能使用Assembly-free方法,就像在式(2)中的Kd运算不需要组装总体刚度矩阵,总体压缩矩阵W也不需要组装,而是采用“相乘然后组装”的方式:
(5)
这种免组装的压缩共轭梯度方法能够高效地处理高达几百万自由度的大型有限元问题[17].
如图 2所示,本文将悬架控制臂的网格模型分为200个组.使用免组装的压缩共轭梯度法求解静力学问题,并得到位移和应力场.
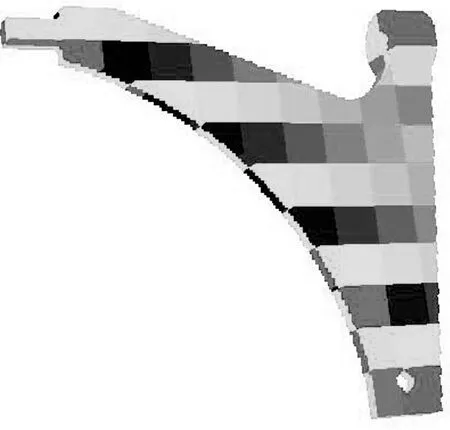
图2 网格分组
2 多工况悬架控制臂拓扑优化
2.1 拓扑灵敏度控制的水平集优化算法
不同于利用伪密度的SIMP方法,本文使用的拓扑优化方法基于拓扑灵敏度.拓扑灵敏度是当拓扑上发生极小的改变时,目标量的变化率.这是由Eschenauer[22]最早研究的,随后诸多学者[23-25]对其进行了扩展研究.
这里通过图 3中的二维例子对拓扑灵敏度进行阐述,研究的目标量是Q,假设结构域某处p去除一个极小的半径为r的小孔,结构的变形将会发生改变,所关心的目标量Q也会改变,拓扑灵敏度TQ定义为[22]:
(6)

图3 二维例子
本文的目标量是柔度J,从公式(6)可以推导出关于柔度拓扑灵敏度[26]的解析表达式:
(7)
式中:TJ为关于柔度J的拓扑灵敏度;p表示网格中的某点;σ为应力张量;ε为应变张量;v为泊松比.
设计域内所有点的拓扑灵敏度构成一个灵敏度场,由定义可知,这个灵敏度场中具有相对较高值的区域表示这个部分对于目标量Q相对重要.使用此拓扑灵敏度场作为水平集,可以用来引入孔洞,确定新的结构域.例如图 4中,引入了一个任意阈值为τ=0.02的“切割”平面,通过式(8)可以确定图 5所示的拓扑结构Ωτ:
Qτ={p|TJ(p)>τ}
(8)
式中的阈值τ是通过当前所需的体积比确定的.结构域Ωτ是所有拓扑灵敏度超过τ的点的集合.
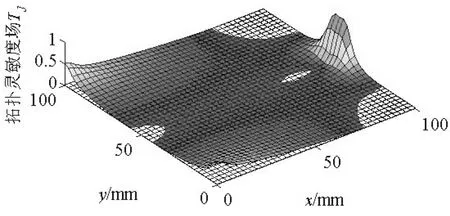
图4 柔度拓扑灵敏度场

图5 结构域Ωτ
然而直接得到的结构域Ωτ并不一定是pareto最优解[13],需要反复进行以下3步:1)对生成的结构域进行有限元分析;2)重新计算拓扑灵敏度;3)根据当前目标体积分数确定新的阈值τ,并生成新结构域.通常这个过程需要3到4次迭代能够收敛[12].收敛之后,可以继续降低当前目标体积分数,重复上述过程,直至得到最终设计要求的体积分数fV0.总体的流程如图 6所示,优化算法的步骤概括为:
①从初始结构Ω=Ω0开始,初始体积V=V0;
②对初始结构Ω0进行有限元分析,通过公式(7)计算拓扑灵敏度;
③按给定的体积减少步长ΔV,确定当前目标体积V=V-ΔV;
④按当前目标体积和拓扑灵敏度场,确定水平集参数τ,使新结构Ωτ的体积等于当前目标体积V;
⑤进行迭代处理:对新结构Ωτ进行有限元分析、计算拓扑灵敏度、得到新结构……直到目标函数J收敛;
⑥判断当前的体积V是否达到最终设计要求的体积fV0,如果没有达到,继续按照步长ΔV降低目标体积分数,返回步骤②;
⑦当前体积达到设计要求的体积分数时,算法终止.

图6 拓扑优化算法流程图
2.2 多工况优化模型
多工况条件下悬架控制臂的拓扑优化模型为
(9)
式中:J为综合目标函数;m为工况总数;Ji为第i个工况的柔度;ωi为第i个工况的权重;V为优化后的体积;V0为结构初始体积;f为体积约束的百分比.
根据各工况的权重系数,可以构造一个新的多工况条件下的拓扑灵敏度:
(10)
式中:Ti为第i个工况下的拓扑灵敏度.
各工况的权重系数可以通过经验法、层次分析法等确定.由于如何选择权重系数并不是本文研究重点,本文重在使用相同的工况和权重系数设置与基于SIMP方法的商用软件作对比.所以本文考虑表 1所示的稳态转向和直线制动两种最基本的工况[27],假设两种工况的权重系数都为0.5.

表1 悬架控制臂工况
对于本文考虑的麦弗逊悬架的下控制臂,在前衬套A和后衬套B通过铰接副与车架相连,在外球销点C通过球形副与转向节相连.主要在加速、制动时承受纵向力Fx,以及在转向时承受侧向力Fy.对于垂向力,下控制臂只是抵消前后橡胶衬套扭转变形时的一些结构反力,而垂向力主要由悬架弹簧来承受,控制臂承受的垂向力的数量级远小于纵向力及侧向力,所以在分析下控制臂时通常不考虑垂向力Fz.分析麦弗逊悬架控制臂时通常固定前衬套X,Y,Z3个方向平动自由度,后衬套Y,Z方向平动自由度,外球销点Z方向平动自由度.制动、转向时的纵向、侧向力分为两个工况施加到外球销点上.
2.3 加工约束
通过拓扑优化方法进行性能最优化设计的结果常常会出现中空的复杂结构,不适合传统加工方法.目前,大多数汽车零部件还是采用传统的方法加工,所以此悬架控制臂的拓扑优化中需要考虑加工制造约束.为了使控制臂结构易于制造加工,在Z方向添加方向约束.具体方法就是对Z方向的各单元的拓扑灵敏度进行额外处理,使外侧单元的拓扑灵敏度不大于内侧单元的拓扑灵敏度,这样就能保证在拔模方向上不会出现中空的结构.值得注意的是,由于使用了体素单元划分网格,网格的排列十分工整,有利于编程实现加工制造约束.
3 优化结果
使用本文方法基于C++语言开发的程序和Hyperworks分别进行拓扑优化,设置相同的材料参数,弹性模量210 GPa,泊松比0.3,使用前文所述的工况设置,网格模型自由度为280 000,目标体积分数为50%.优化后的结果分别如图 7 (a) (b)所示.图 8给出了优化过程中两种工况下的柔度变化曲线,以及优化过程中的一些拓扑结构和应力云图.
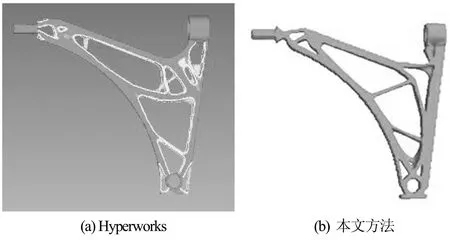
图7 优化结果
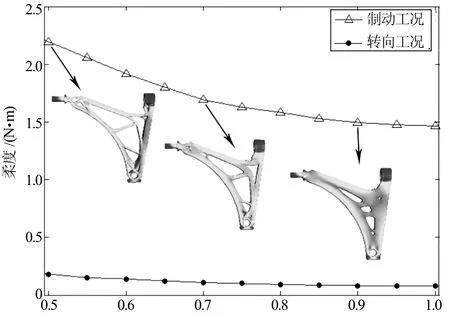
体积分数
两种方法的最优拓扑略有不同,但除了一些细小结构的区别,主要的材料分布趋势是近似的.根据最优拓扑提供的参考,对结果进行几何重构后如图9所示,性能对比如表2所示.

图9 几何重构后的结构
表2 性能对比
Tab.2 Property comparison
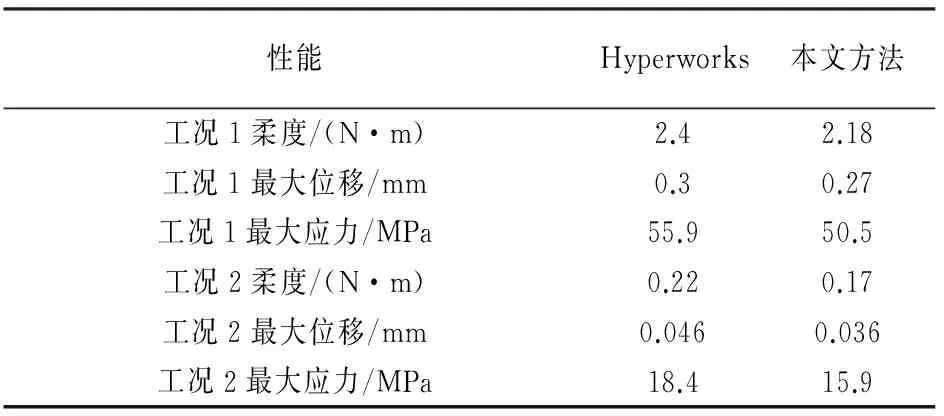
性能Hyperworks本文方法工况1柔度/(N·m)2.42.18工况1最大位移/mm0.30.27工况1最大应力/MPa55.950.5工况2柔度/(N·m)0.220.17工况2最大位移/mm0.0460.036工况2最大应力/MPa18.415.9
注:计算时间Hyperworks方法为74 min,本文方法为19 min.
通过表 2中各工况的柔度、最大位移、最大应力的对比可知,两种结构的性能接近,且本文方法优化的结构性能略优于Hyperworks优化的结果.而在计算时间上,两种方法有很大不同,本文方法是Hyperworks的26 %,可见对于大自由度的模型,本文方法有明显的速度优势.这主要是由于DCG算法对有限元求解的加速作用.图10表明了使用不同分组数的DCG算法的收敛性,分组数量的不同导致DCG运算收敛所需的迭代次数不同.如图所示,分成200组比未分组的CG运算所需的迭代次数大幅降低,这意味着单次有限元分析所需的时间大幅降低,从而缩短了整个拓扑优化过程的时间.不同分组数下相应的拓扑优化时间如表3所示.

迭代次数
表3 不同分组下的优化时间
Tab.3 Optimization time with different groups

分组数优化时间/min06950511003220019
此外,对于复杂结构,商用软件需要人工进行几何分解、网格划分、网格质量检查等步骤,直到满足商用软件的特定要求后才能开始拓扑优化.而本文方法采用体素化网格实现自动网格划分,在拓扑优化的前处理阶段就可以节省大量的时间.
4 结 论
本文将一种基于拓扑灵敏度的拓扑优化算法与免组装压缩共轭梯度法结合,提高了大型三维拓扑优化的速度,通过添加多工况优化和加工约束功能,使其更适合实际工程应用.通过悬架控制臂的多工况优化,与基于SIMP方法的商用软件对比,结果表明,该算法具有明显的速度优势,且能获得性能相近的结构.由于拓扑优化是初始的概念设计,体素化网格的精度局限性对拓扑优化结果并不会产生很大影响,而速度优势可以在前处理阶段以及拓扑优化阶段得到很好的发挥.在未来的研究中,可以拓展更全面的优化功能,使该算法能更好地满足实际工程应用的要求.
[1] SIGMUND O. A 99 line topology optimization code written in Matlab[J]. Structural & Multidisciplinary Optimization, 2001, 21(2):120-127.
[2] HUANG X, XIE Y M. A new look at ESO and BESO optimization methods[J]. Structural & Multidisciplinary Optimization, 2008, 35(1):89-92.
[3] MUNK D J, VIO G A, STEVEN G P. Topology and shape optimization methods using evolutionary algorithms: a review[J]. Structural & Multidisciplinary Optimization, 2015, 52(3):613-631.
[4] MEI Y, WANG X. A level set method for structural topology optimization and its applications[J]. Advances in Engineering Software, 2004, 35(7):415-441.
[5] DIJK N P V, MAUTE K, LANGELAAR M,etal. Level-set methods for structural topology optimization: a review[J]. Structural & Multidisciplinary Optimization, 2013, 48(3):437-472.
[6] BENDSØE M P, SIGMUND O. Material interpolation schemes in topology optimization[J]. Archive of Applied Mechanics, 1999, 69(9/10): 635-654.[7] ROZVANY G I N. A critical review of established methods of structural topology optimization[J]. Structural & Multidisciplinary Optimization, 2009, 37(3):217-237.
[8] 祝小元,方宗德,申闪闪,等. 汽车悬架控制臂的多目标拓扑优化[J]. 汽车工程, 2011, 33(2): 138-141.
ZHU Xiaoyuan, FANG Zongde, SHEN Shanshan,etal. Multi-objective topology optimization for the control arm of vehicle suspension[J]. Automotive Engineering, 2011, 33(2): 138-141. (In Chinese)
[9] 兰凤崇,张浩锴,王家豪,等. 汽车转向节拓扑优化方法研究及应用[J]. 汽车工程, 2014, 36(4): 464-468.
LAN Fengchong, ZHANG Haokai,WANG Jiahao,etal. Study and application of topology optimization technique for vehicle steering knuckles[J]. Automotive Engineering, 2014, 36(4): 464-468. (In Chinese)
[10]朱剑峰,林逸,施国标,等. 考虑工程约束的发动机悬置支架拓扑优化[J]. 汽车工程, 2014, 36(12): 1508-1512.
ZHU Jianfeng, LIN Yi, SHI Guobiao,etal. Topology optimization of engine mount bracket with consideration of engineering constraints[J]. Automotive Engineering, 2014, 36(12): 1508-1512. (In Chinese)
[11]张伟, 侯文彬, 胡平. 基于拓扑优化的电动汽车白车身优化设计[J]. 湖南大学学报:自然科学版, 2014,41(10):42-48.
ZHANG Wei, HOU Wenbin, HU Ping. The body in white optimization of an electric vehicle using topology optimization[J]. Journal of Hunan University:Natural Sciences, 2014,41(10):42-48. (In Chinese)
[12]SURESH K. Efficient generation of large-scale pareto-optimal topologies[J]. Structural & Multidisciplinary Optimization, 2013, 47(1):49-61.
[13]SURESH K. A 199-line matlab code for pareto-optimal tracing in topology optimization[J]. Structural & Multidisciplinary Optimization, 2010, 42(5):665-679.
[14]INNA T, KRISHNAN S. Efficient generation of pareto-optimal topologies for compliance optimization[J]. International Journal for Numerical Methods in Engineering, 2011, 87(12):1207-1228.
[15]HUGHES T J R, LEVIT I, WINGET J. An element-by-element solution algorithm for problems of structural and solid mechanics[J]. Computer Methods in Applied Mechanics & Engineering, 1983, 36(2):241-254.
[16]YADAV P, SURESH K. Assembly-free large-scale modal analysis on the graphics-programmable unit[J]. Journal of Computing & Information Science in Engineering, 2013, 13(1):1-11.
[17]YADAV P, SURESH K. Large scale finite element analysis via assembly-free deflated conjugate gradient[J]. Journal of Computing & Information Science in Engineering, 2014, 14(4): 1-9.
[18]KARABASSI E A, PAPAIOANNOU G, THEOHARIS T. A fast depth-buffer-based voxelization algorithm[J]. Journal of Graphics Tools, 1999, 4(4): 5-10.
[19]DÜSTER A, PARVIZIAN J, YANG Z,etal. The finite cell method for three-dimensional problems of solid mechanics[J]. Computer Methods in Applied Mechanics & Engineering, 2008, 197(45/48):3768-3782.
[20]AUBRY R, MUT F, DEY S. Deflated preconditioned conjugate gradient solvers for linear elasticity[J]. International Journal for Numerical Methods in Engineering, 2011, 88(11): 1112-1127.
[21]SAAD Y, YEUNG M, ERHEL J,etal. A deflated version of the conjugate gradient algorithm[J]. Siam Journal on Scientific Computing, 1998, 21(5): 1909-1926.
[22]ESCHENAUER H A, KOBELEV V V, SCHUMACHER A. Bubble method for topology and shape optimization of structures[J]. Structural & Multidisciplinary Optimization, 1994, 8(8):42-51.
[24]STOLPE M, STIDSEN T. A hierarchical method for discrete structural topology design problems with local stress and displacement constraints[J]. International Journal for Numerical Methods in Engineering, 2007, 69(5):1060-1084.
[25]RAMANI A. Multi-material topology optimization with strength constraints[J]. Structural & Multidisciplinary Optimization, 2011, 43(5):597-615.
[26]GIUSTI S M, NOVOTNY A A, PADRA C. Topological sensitivity analysis of inclusion in two-dimensional linear elasticity[J]. Engineering Analysis with Boundary Elements, 2008, 32(11):926-935.
[27]上官文斌,蒋翠翠,潘孝勇. 汽车悬架控制臂的拓扑优化与性能计算[J]. 汽车工程, 2008, 30(8): 709-712.
SHANGGUAN Wenbin, JIANG Cuicui, PAN Xiaoyong. Topology optimization and performance calculation for control arm of vehicle suspension[J]. Automotive Engineering, 2008, 30(8): 709-712. (In Chinese)
Topology Optimization of Suspension Control Arm Based on Assembly-free Finite Element Method
BIAN Xiang†, FANG Zongde
(Department of Mechanical Engineering, Northwestern Polytechnic University, Xi’an 710072, China)
A suspension control arm was optimized by topology optimization under multi-working condition. In order to improve the speed of topology optimization for practical engineering problems, a topology optimization method based on topological sensitivity was combined with an assembly-free finite element method. The structure was discretized via uniform voxels. A deflated conjugate gradient (DCG) method was used to accelerate the finite element analysis. After the finite element analysis, the stress and strain field can be used to generate the topological sensitivity field, and the topological sensitivity field can be used to control the change of topology. Multi-working condition optimization and manufacturing constraints were used to make the method more suitable for practical problem. The comparison shows that the method can result in the close performance and similar shape of optimized structure to the commercial software. Meanwhile, the speed of the entire optimization is increased significantly.
suspension control arm; topology optimization under multi-working condition; assembly-free finite element method; voxelization; deflated conjugate gradient; topological sensitivity
1674-2974(2017)04-0023-07
10.16339/j.cnki.hdxbzkb.2017.04.004
2016-05-27
国家建设高水平大学公派研究生项目(留金发[2013]3009),National Constructed High-level University Sponsored Graduate Program([2013]3009)
卞翔(1988-),男,江苏南京人,西北工业大学博士研究生†通讯联系人,E-mail:bianxiang3@hotmail.com
U463.33
A

