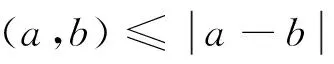数论中的五类不等式问题
吕孙忠
浙江省宁波效实中学 (315012)
数论中的五类不等式问题
吕孙忠
浙江省宁波效实中学 (315012)
不等式和数论结合的试题,需要有较强的代数变形技巧,以及一部分整数方面的知识.文中的符号如下:

(a,b)和[a,b]分别表示a和b的最大公约数和最小公倍数;
[x]和{x}分别表示x的整数部分和小数部分;
d(n)和σ(n)分别表示整数n的约数个数和约数和.
1 k进制中的不等式问题
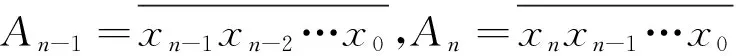

注:这是一道以k进制为背景的不等式题目,其本质还是通过逐项比较判断符号.其中,涉及到的一个性质是AnBn-1=(xnan+An-1)Bn-1.
例2f(n)表示n!含的2的指数,其中n为正整数,证明:(1)f(n) ∴n-(x0+x1+…+xk)≥a-(y0+y1+…+yi)+b-(z0+z1+…+zj),⟺a+b≤n+(y0+y1+…+yi)+(z0+z1+…+zj)-(x0+x1+…+xk)≤n+(i+1)+(j+1)-1=n+(i+j)+1≤n+2k+1,且2k 注:从表面上看例3,大多数人会不知道如何入手,如果将问题表示为二进制以后,那么问题就柳暗花明了. A1=[x]≤[1·x],假设Ai≤[ix]成立(i=1,2,…k).A1=[x],2(A2-A1)=[2x],…,(k+1)(Ak+1-Ak)=[(k+1)x],∴(k+1)Ak+1-(A1+A2+…+Ak)=[x]+[2x]+…+[(k+1)x].又∵[x]+[y]≤[x+y],∴(k+1)Ak+1≤([x]+[kx])+([2x]+[(k-1)x])+…+([kx]+[x])≤(k+1)[(k+1)x],∴Ak+1≤[(k+1)x],∴对任意自然数n,An≤[nx]. 注:此题直接使用第一数学归纳法是行不通的,要使用第二数学归纳法,借助一个数论不等式[x]+[y]≤[x+y],最后通过倒写相加解决问题. 注:利用整数的离散性,a,b∈Z,a>b,则a≥b+1. 注:整数的离散性,还表现在一些平方数或者立方数的差,它们的间隔会有一定的特点,只能取到某些特定的数. 例11d(n)表示n的约数个数.求证: 注:此题也需要交换求和符号,同时也考察了σ(n)的两种表示方式. 注:此题中在化简的时候除了用到均值不等式以外,还用到了两条数论的性质,它们分别是(a,b)≤|a-b|和(ak,bk)=(a,b)k.看到此题要证明的结论,其实可以从结论出发,猜测证明的过程(a3,b3)≥(a,b)3≥|a-b|3>3ab,然后再进行代数变形,得到所需要的a3和b3. [1]边红平.初等数论[M].浙江大学出版社,2007. [2]何忆捷.数论性质在不等式问题中的应用[J].中等数学,2014,01:5-9. [3]羊明亮.2014中国西部数学邀请赛[J].中等数学,2014,11:31-34. [4]刘康宁.数论中的不等式问题[J].中等数学,2010,01:9-13.

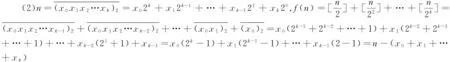




2 高斯函数中的不等式问题







3 离散性中的不等式问题


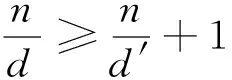




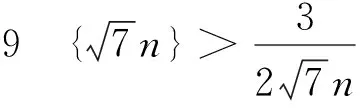


4 σ(k)函数中的不等式问题






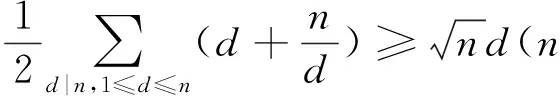
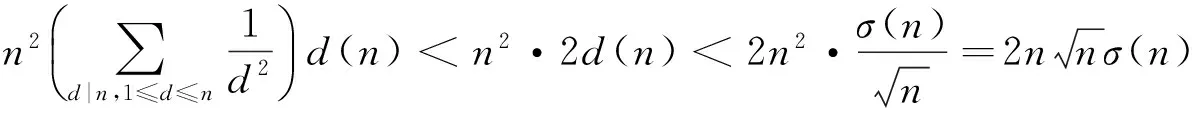



5 公约数和公倍数中的不等式