《数学通报》2305问题的证明及推广
张留杰 宋其云
北京市陈经纶中学 (100020)
《数学通报》2305问题的证明及推广
张留杰 宋其云
北京市陈经纶中学 (100020)
2305问题AB是圆锥曲线mx2+ny2=1的斜率等于1的弦,AB的垂直平分线与该圆锥曲线交于点C、D,则A、B、C、D四点共圆.[1]
拜读本刊数学问题解答2305问题之后,引发了笔者深深思考,虽然题目条件中的有心圆锥曲线具有很强的一般性,但是对弦AB和直线CD的条件要求十分特殊,该问题背后是否存在一般规律呢?该结论对抛物线是否成立?带着这些思考开启了下面的探究之旅.
一、问题的证明
该问题所给的解答中,充分利用了“CD垂直平分AB”这一几何特征,取CD的中点F(如图1),从而确定这四点共圆的充要条件是BF为圆的半径,进而得出等价条件|CD|2-|AB|2=4|EF|2,然后用解析法证明该等式,凸显了解析几何的本质,即用代数的方法解决几何问题.
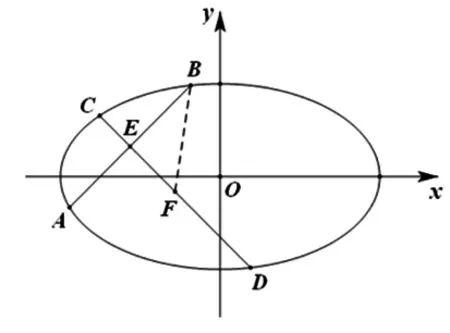
图1
如果不添加辅助线,设AB与CD的交点为E,直接证明|EA|·|EB|=|EC|·|ED|,能够回避求线段长度的繁琐过程,会显得更加简捷.
证明:设E(x0,y0),直线AB的方程为y=x+t,则y0=x0+t,因为CD⊥AB,则直线CD的方程为y-y0=-(x-x0),即y=-x+2x0+t.
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
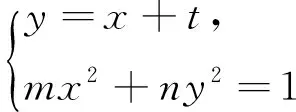
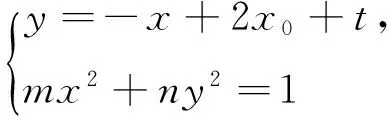
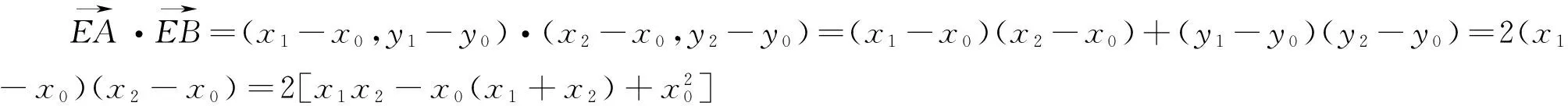

=|EC|·|ED|,所以A、B、C、D四点共圆.
二、问题的推广
根据上述证明过程,笔者发现“点E是AB中点”这一条件可以省去,然后根据有心圆锥曲线的对称性,可以得出如下结论:
结论1AB是圆锥曲线mx2+ny2=1的斜率为k的弦,若|k|=1,垂直于直线AB的直线l与圆锥曲线交于点C、D,则A、B、C、D四点共圆.
波利亚在《怎样解题》中指出“数学问题的解决仅仅只是一半,而更重要的是解题之后的回顾与反思.”再次回顾该问题,总感觉还有更一般性的规律,究竟由哪个条件进行引申推广呢?经过一番思考,决定从AB和CD的斜率或倾斜角进行探究.
命题1 若A、B、C、D为有心圆锥曲线mx2+ny2=1(m≠n)上四个不同的点,且直线AB与直线CD相交于点E,α、β分别为直线AB、CD的倾斜角,试探究当A、B、C、D四点共圆时,α与β的关系.


结论2 若A、B、C、D为有心圆锥曲线mx2+ny2=1(m≠n)上四个不同的点,且直线AB与直线CD相交于点E,则A、B、C、D四点共圆的充要条件是直线AB与CD的倾斜角互补.
类似地,也很容易将该结论推广到抛物线中.
所以根据2305问题我们可以得出圆锥曲线上四点共圆的一个重要定理,凸显了该问题背后深刻的内涵和其使用价值.
定理A、B、C、D为圆锥曲线W上四个不同的点,且直线AB与直线CD相交于点E,则A、B、C、D四点共圆的充要条件是直线AB与CD的倾斜角互补.
[1]张国坤.数学问题解答2305题[J].数学通报,2016.6.

