巧用“三结合”，润色数学课堂

陈国勇　郭小龙

一、新旧结合。构建支架

在小学阶段的数学，很多新知识都可以在已学的知识中找到最近发展区，但是对于学生来说，他们还没有足够的能力将新旧知识联系起来，这时就需要教师及时复习旧知，让学生将旧知迁移到新知的学习当中，架起新旧知识的桥梁。同时，在学完新知后要让学生对旧知进行一个全面的回顾，完善所学的知识，让新旧知识串成一条线，在大脑里形成知识网络，从而帮助学生成功抵达知识的彼岸。

1.旧知到新知的迁移，激起学习兴趣。

旧知是新知的铺垫，新知是旧知的深入。在数学课堂中，运用好新知与旧知的共同点，加强新旧知识的联系是非常重要的，这将激起学生学习的兴趣，降低学习的难度，提高课堂的学习效率。

执教四上“大数的认识”，这一课要求学习四个计算单位，面面俱到肯定不是最佳策略。我们应该找到新旧知识的连接点，以“十万”为突破口，引导学生以旧探新，展开积极主动的学习过程。

首先，我们可以选择生活素材，从复习旧知引入，唤醒学生对旧知的记忆，同时激发学生学习新知的兴趣。先展示人口普查数据等能够充分体现出大数的资料，让学生感受生活中大数的存在。接着，结合计数器使学生认识计数单位。先从一千一千地数，数到10个一千时，让学生知道要向万位进一。再在万位上一颗一颗地拨，拨到10个时，又要怎么办？学生自然而然地知道要向前一位进一。这样的教学，让学生从旧知到新知的学习有一个正向的迁移，沟通了新旧知识间的联系，真正做到了“启”而能“发”1

2.新知到旧知的回顾，加深知识理解。

旧知到新知的迁移固然重要，但是学完新知再回过头来看旧知也同等重要，它能够帮助我们建构全面的知识网络，能够让我们以全新的角度重新理解旧知。

在教学人教版四下“乘法分配律”时，笔者在让学生发现乘法分配律这一规律后，也对知识进行了相应的巩固。之后笔者设计了一个问题：“在你们之前学过的知识中你知道在哪里有运用到乘法分配律？”学生开动大脑进行思考，发现在学习乘法计算的过程中有用到。一位学生说：“例如在列竖式计算15x12时，12可以看成10+2的和，15x12其实就是15x10与15x2的和。”笔者继续追問：“再想想，在哪里还出现过？”学生这时出现思维障碍。笔者此时出示一个长方形（长10cm，宽8cm），提问：“长方形的周长是多少？”接着让2位同学到黑板上展示做法。第一位同学：（10+8）x2=36（cm），第二位同学：10x2+8x2=36（cm）。笔者提问：“请同学们仔细观察这两个算式，你发现了什么？”这时，学生恍然大悟，在计算长方形的周长时，实际上已经运用到乘法分配律。借助学习乘法分配律的机会使学生对旧知又有了进一步的理解。

因此，在数学课堂中，教师要合理组织教学活动，在教学的每一个环节注意新旧知识间的联系，教师要时刻考虑引导学生利用已有的知识促进对新知的学习，同时还要让学生利用新知加强对旧知的理解。要做到“瞻前顾后”与“边学边回头”，让已学和新学的知识有机地结合起来，组成一个结构完整的知识体系。新旧知识的结合，将会促进学生思维的提高和发展，也将会让整个数学课堂得到完美的提升！

二、正反结合。辩证融通

课堂教学永远是一门有缺憾的艺术。一堂设计再好的课，不同的学生始终会有不同的反应。课堂上的教学资源是处于一个动态生成的过程，既有正确的资源，也有错误的资源，教师应该发挥教学机智，善于抓住学生生成的资源，暴露学生的易错点，突破教学的重难点。课堂上不能为了赶进度而一味地出示正确的资源，也不能一直捕捉错误资源而没有指给学生正确的方向。真正的课堂，应该做到正反资源的有效结合，允许学生出错，鼓励学生尝试，同时也应该给予他们正确的指引。

笔者执教四上“角的度量”这一课，在教学进行到用18等分的半圆工具度量角时，设计了一道题目，让学生动手量。（图1）

首先展示：量出来有6个小角。学生举手说：“不同意，因为这个角比直角大，6个小角是错的。”接着，再让量出来是12个小角的学生上台展示，并说出量角的步骤。笔者追问：“刚才那位同学量出来为什么是6个小角，你能帮他分析一下吗？”学生马上说：“他数错方向了，这题中角的边是和量角器的左边重合，要从左边数起。”正反资源的有效结合，让学生更好地掌握量角的方法。

正确资源的学习能够得出方法，错误资源则更能引起思考。我们应该以全新的观念，全新的眼光，让学生在正确中学，在错误中成长，将正反加以融合，帮助学生更准确地掌握所学内容，预防错误的出现。

三、“基”“能”结合。拓展思维

《课程标准》中明确提出，义务教育阶段的数学学习要注重培养学生的“四基”与“四能”。在小学数学的学习中，第一目标就是让学生掌握好数学的基础知识，在夯实基础的同时再来提高和拓展学生的数学思维能力。

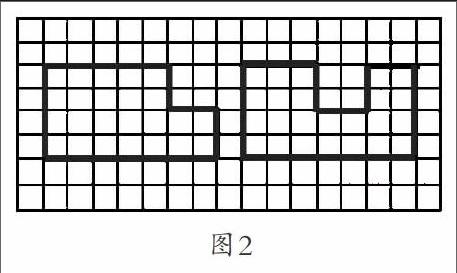
笔者在执教三上“整理和复习：周长”这一课时，主要围绕“周长在哪里？”与“怎么求周长？”这两个核心问题帮助学生对所学的周长知识进行梳理，让他们进一步理解周长的意义。梳理完周长的知识，笔者设计了一道题：比一比，图2两个图形的周长一样长吗？（图中每个小正方形的边长是1厘米）

此题的设计是在学生对于周长知识掌握牢固的情况下进行的，解决策略可以是采用“数一数”，也可以采用平移的方法。既能够让学生掌握基本的方法，又能够发散学生的思维，他们可以选择适合自己的方法来解决问题，真正做到在基础上拓展数学思维。

夯实基础是根本，提高能力是关键。数学课堂不仅仅要让学生掌握基础知识，还要提高他们对知识的应用和理解。“基”与“能”的结合，能够优化课堂教学，提高课堂效果，能够使数学课堂更具层次性，从而更具“能量”！