机械能守恒定律剖析

许曦普

枣庄市第三中学 山东枣庄 277101

机械能守恒的前提：“只有在重力或弹力做功的物体系统内，必须是动能和势能的相互转化，且总的机械能保持不变”。我们从中可以概括出机械能守恒的条件是：第一，在一个系统内；第二，只有重力或弹力做功；第三、只有动能和势能的相互转化；第四、机械能总和不变。切记这里的只有重力或弹力做功并非是除了这二者外其他的力对系统不能做功，当其他的力对系统做了功且做功的代数和为零时整个的系统机械能照样守恒。例如“一架吊车吊起一重物上升”的过程，重物上升过程中除重力做功吊绳的拉力也做了功，且无重力做功之外的其他力做功和拉力做的功相抵消，既其它力做功的代数和不为零，重物的机械能不守恒。能量转化的角度来看，在这一过程中除了动能与势能的相互转化以外，还存在其它形式的能与机械能的转化。

再例如：一轻质弹簧一端固定在竖直的墙上，另一端与一质量为m的物体相连，放在粗糙的水平面上，先压缩弹簧然后释放。弹簧与物体组成的系统在整个运动过程中，除了弹簧的弹力做功以外还存在物体与水平面的摩擦力做功，物体要克服摩擦力做功消耗一定的机械能去转化为内能，所以系统的机械能减小，机械能不守恒。由此可知，在一个物体系统内，除了重力或弹力做功以外其它力做功的代数和不为零时则系统的机械能将发生变化。再例如：一质量为m的物体静止放在粗糙的斜面上，给物体一个平行于斜面向下的推力作用且该推力大小等于滑动摩擦力大小，那么该物体在下滑的过程中其机械能是守恒的。因为在下滑中除重力外、外力中的摩擦力与外力中的推力都对物体做了功，但是它们所做功的代数和为零，因此物体所在系统的机械能仍是守恒的。那么机械能的变化与外力（除了重力或弹力以外的力，后面都称为“外力”）做功存在什么关系呢？下面我们通过推导来寻找。

一架吊车用力F把质量为m的物体吊起，当物体距地面高度为h1时速度为v1，当距地面高度为h2时速度为v2，求物体从h1到h2过程中拉力F做的功。

解析：物体上升的过程中受到重力和拉力，并且两个力都做功，由动能定理得：

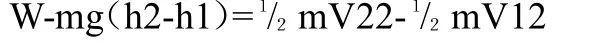
其中1/2mV22+mgh2为物体末状态的机械能，mV12+mgh1为初状态的机械能。这个公式说明：在一个物体系统内，外力做功等于系统机械能的变化量。

结论：在一个物体系统内除了重力或弹力以外的其它力做功代数和不为零时，则系统的机械能不守恒，外力所的做功等于机械能的变化量。外力做正功机械能增加，增加的机械能等于外力所做的功；外力做负功机械能减少，减少的机械能等于物体克服外力所做的功。

例1.质量为m的物体，从静止开始以g/2的加速度竖直下落h的过程中，以下说法正确的是（ ）

A．物体的机械能守恒

C．物体的重力势能减少mg h

解析：由物体下落的加速度可知物体下落时受到重力的同时还受到一外力（阻力）作用，并且这个除了重力外的外力对物体做功的代数和不为零，所以物体的机械能不守恒；这个外力（阻力）对物体做负功，由上面的结论可知物体的机械能减少。由牛顿第二定律可得阻力f=mg/2，所以物体克服阻力做功为mg h/2，物体机械能减少mgh/2；重力做功mgh，则重力势能减少mg h。既本题目答案是BCD。

例2.已知：具有一定初速度的物体，沿倾角为30°的粗糙斜面向上运动的过程中，受一个恒定的沿斜面向上的拉力F的作用，这时物块的加速度大小为4m/s2，方向沿斜面向下，那么物块向上运动过程中，正确的说法是（）

A．物块的机械能一定增加

B．物块的机械能一定减少

C．物块的机械能可能不变

D．物块的机械能可能增加也可能减少

解析：本题中的物体受到重力、斜面的支持力、摩擦力和拉力，其中除了支持力不做功外，其它力都对物体做功，摩擦力做负功，拉力做正功。若两个力的功的代数和为零，则物体的机械能不变，若不为零物体的机械能就发生变化。所以这个题目转化为比较摩擦力和拉力的大小。对物体由牛顿第二定律可得：

mgsin30°+f-F=ma

所以F=mgsin30°+f-ma由已知条件可得拉力大于摩擦力，所以拉力与摩擦力的合力做正功，物体的机械能增加，答案是A。

通过上面几个例题可以看出，对“除了重力或弹力以外的力做功改变系统的机械能”的考查往往与其它的功能关系同时出现在选择题，学生只要掌握了这些功能关系，这类题目就迎刃而解了。

参考文献：

[1]中学物理教学参考，人民教育出版社，2017：14-16.