数学思想与知识在理科中的运用

袁 浩

合肥市第一中学 安徽合肥 230001

数学作为一门偏难但又是十分重要的基础科目，其重要性毋庸置疑，并且数学的思想方法可以运用至物化生等科目中。若将其知识联系，那么在学习其他科目时也将事半功倍。然而颇为遗憾不少同学们在理科的学习中将科目划限，不联系其间的关联性，导致学习效果不佳。一个科目的精髓是其思想方法，而数学思想与知识又被运用极为广泛，若能充分且巧妙地运用数学工具，那么在学习其他科目时会对同学们有所帮助。笔者试通过对不同的数学思想方法按类划分，运用理科例题，具体而微地论述数学思想与知识的运用。

一、运用图形数学

图形数学是人们较早接触并用于简化问题的一种思想，其目的是将所研究问题化难为易，化繁为简。运用好图形，难以运算代换的问题或许将得到轻松的解决。

例一：不少同学恐怕一直认为f-x求摩擦力简单，然而遇到一些题目力与路程关系式难以表示时，便会捉襟见肘。

如图1，质量为m的小车以恒定速度v沿半径为R的轨道运动，已知f、k，则小车由最低运动至最高，摩擦力做功为多少？

对其运动过程中一点作受力分析可知小车受四个力，作图2受力分析图像。

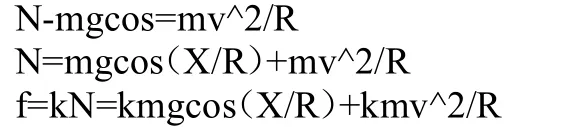
对称轴X=k R(k∈Z)

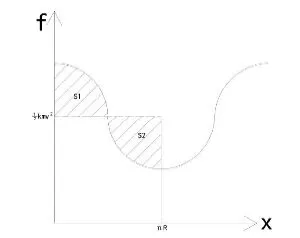
图3

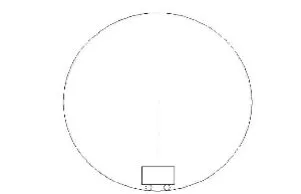
图1

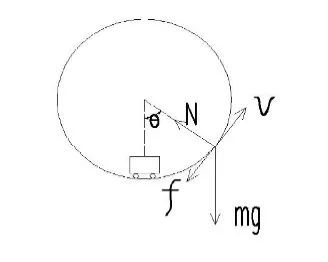
图2

根据以上方程可作图3，根据余弦函数性质S1=S2

此时利用填补法将S1填入S2得，Wf=-k mv2

例二：很多同学觉得s-t图像简单，可是若能用活s-t图也是大有助力的。

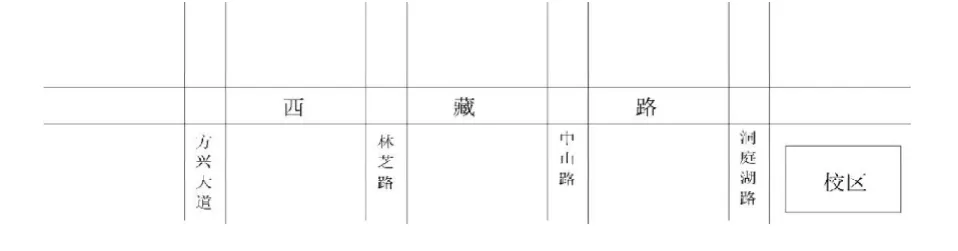
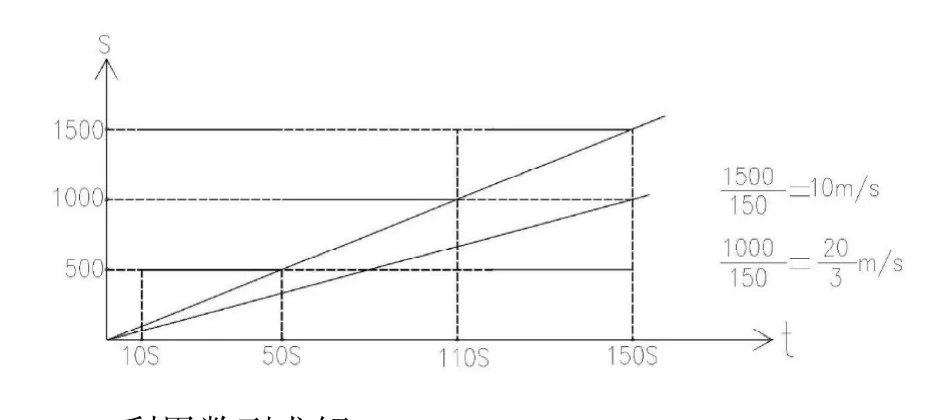
如图为一交通路线图，每个路口间距500米，每个红绿灯设计是：红灯亮40秒，绿灯亮60秒，相邻两路口绿灯熄灭间隔时间为50秒（黄灯亮起算为红灯时间）某同学家长从方兴大道方向送小孩来校区上课，假设刚好到达方兴大道路口时，绿灯刚好亮起，若要一路绿灯到达校区，假设车匀速行驶，则最大速度与最小速度分别为多少？要求 v控制在15km/h-60km/h。在图中虚线代表绿灯时期，实线代表红灯时期，斜线则为匀速运动曲线图。若斜线遇到实线则无法通过，而遇到虚线则可以通过，调整斜率即可得到斜线连续通过四个路口的最大斜率与最小斜率，即为其速度极值。

二、利用数列求解

数列知识是高中重要内容，然而现在高考却将其难度削减，数列的应用比较广泛，以下为笔者学习阶段所遇较复杂的迁移应用。

例一：5人互送礼品有多少种组合方式？

设人为12345，礼品为ABCDE

1 2 3 4 5

A B C D E

假设1选择B那么分为两种情况：（1）2选择A那么便成立345错排。（2）2不选A则可看做4人错排。

这在高中是很常见的题目，相信不少同学都有所接触，但深究其源，终有所获。

三、小结

除上述思想外还有函数方程思想、整体思想、化归思想、归纳推理思想、类比思想等。而数学的知识更是为笔者看重，不过数学思想与知识的运用并不是孤立的，而是相互交错，只要通过不断练习便能整合这些思想与知识点，最大化发挥出数学的作用。数学世界何其精彩广阔，数学思想引导这一代代学者去探索前行，就连著名数学家物理学家牛顿都自认为自己是个在科学的海岸边捡拾石子的小孩。笔者的这点探索在数学海洋中更微不足道。但正因为无数先辈艰苦卓绝地奋斗才有如今辉煌的成果。著名数学家华罗庚只有初中学历，却凭借自己对数学的无穷热爱成为数学领域的巨人。而笔者也不断地向着巨人的肩膀攀登，如诸多同仁一样向着科学行进。