初中数学教学中渗透化归思想的研究*

广东省佛山市南海区大沥镇黄岐初级中学(528248) 林奎枢

初中数学教学中渗透化归思想的研究*

广东省佛山市南海区大沥镇黄岐初级中学(528248) 林奎枢

转化与化归的思想方法是数学中最基本的思想方法.数学中一切问题的解决(当然包括解题)都离不开转化与化归,数形结合思想体现了数与形的相互转化;函数与方程思想体现了函数、方程、不等式间的相互转化;分类讨论思想体现了局部与整体的相互转化,以上三种思想方法都是转化与化归思想的具体体现.各种变换方法、分析法、反证法、待定系数法、构造法等都是转化的手段……所以说,转化与化归是数学思想方法的灵魂.

一、对数学化归思想的进一步认识

引例:“南海区2013-2014学年度第一学期期末考试八年级数学试卷”的第24题:如图,已知A、B两村庄的坐标分别为(2,2)、(7,4),一辆汽车在x轴上行驶,从原点O出发．

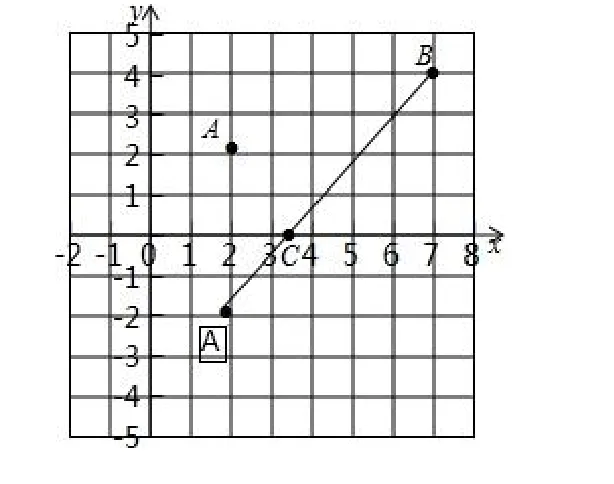
图1

(1)汽车行驶到什么位置时离A村最近?写出此点的坐标．

(2)汽车行驶到什么位置时离B村最近?写出此点的坐标．

(3)汽车行驶到什么位置时,距离两村的和最短?请在图中画出这个位置,并求出此时汽车到两村距离的和．

分析:(1)、(2)根据垂线段最短,可得答案;

(3)根据“线段垂直平分线上的点到线段两端点的距离相等”可作A点关于x轴的对称点,根据两点之间线段最短,可得答案．

点评:本题考查了最短路线问题,先作出A点的对称点A′,连接A′B,最短路线问题转化(即是化归)为求线段连接A′B的长度了.

化归常常是实际问题与数学模型之间的转化.数学模型是从现实世界中抽象出来的,是对客观事物的某些属性的一个近似的反映,但对解决实际问题而言,数学模型却是深刻、正确、完善地反映着现实.因此,把所考察的实际问题,化归为数学问题,构造相应的数学模型,通过对数学模型的研究,使实际问题得以解决,充分地体现了“用数学”的意识和能力.请看以下关系:

匈牙利著名数学家P.路莎曾指出:“数学家的思维过程是很典型的,他们往往不是对问题进行正面的进攻,而是不断地将它变形,直至把它转化为已经能够解决的问题”这位数学家所说的不断将它变形直至把它转化为已经能够解决的问题的过程事实上就是化归.

二、初中数学教学中渗透化归思想的重要性

化归是解决问题的一种最基本的思想方法,是中学数学最基本的思想方法之一,堪称数学思想的精髓,它渗透到了数学教学内容的各个领域和解题过程的各个环节中.数学大师波利亚说:解决问题需要不断地变换,需要一再变化它,重新叙述它,直到最后成功地找到某些有用的东西为止,…….波利亚精辟地叙述了化归思想方法的重要性.实际上,我们常常是把将要解决的陌生问题通过化归,变为一个比较熟悉的问题来解决,因为这样可以充分调动和运用我们已有的知识、经验和方法应用于问题的解决,也常常将一个复杂问题化归为一个或几个简单的问题来解决,或将抽象的问题化归为具体的问题来解决,等等,这就是化归的思想方法.化归的思想方法已渗透到整个教学内容及解题过程中,它也是平时考试乃至中考的重点考查对象,对考生的要求也越来越高,化归思想是数学的灵魂,它在培养学生的数学素质和解题能力方面起到了很重要的作用.因此理应引起充分重视.

三、初中数学的化归数学思想运用的题型举例

著名的数学家,莫斯科大学教授C.A.雅洁卡娅曾在一次向数学奥林匹克参赛者发表《什么叫解题》的演讲时提出:“解题就是把要解题转化为已经解过的题”.数学的解题过程,就是从未知向已知、从复杂到简单的化归转换过程.下面我就通过举例说明在初中数学教学中所渗透的化归数学思想.

(一)数(式)与数(式)之间的转化

例1:(北师大八年级下第104页第1(7)题改编):分解因式:9(a−b)2−(a+b)2

分析: 首先把3(a−b)和(a+b)看成整体,转化为用平方差公式进行分解,再把括号里的同类项进行合并,观察发现括号里还用公因式,再提公因式即可．

点评: 此题主要考查了公式法分解因式与提公因式法分解因式,熟练掌握平方差公式的结构特点是解题的关键,把3(a−b)和(a+b)看成整体,转化为用平方差公式进行分解,注意分解因式要彻底．

例2:已知x+y=3,且xy=−1,则x2+y2=

分析: 根据完全平方公式展开,可得x2+y2= (x+y)2−2xy,再把x+y、xy的值代入计算即可．

点评:本题考查了完全平方公式,注意可以根据完全平方公式转化(化归)x2+y2为(x+y)2、2xy的等量关系．

(二)形与形之间的转化

比如:利用图象变换的知识作出函数图象;利用分割、补形、折叠、展开,作辅助线,辅助面处理空间图形或平面图形,包括把立体问题化归为平面问题等等.

例3:请看南海区2012-2013学年度第二学期七年级数学期末绿色指标监测卷的第24题:

图2

图3

图4

如图,建筑工人经常要测量两堵围墙所成的∠AOB(如图,不是直角)的度数与外墙根部两点A、B之间的距离,但人不能进入围墙,又不能站在墙上,只能站在墙外.现有量角器和皮尺两种工具,聪明的你帮助工人师傅想想办法吧．

(1)请你设计一个写出测量∠AOB的方案,在(1)上画图,并说明理由．

(2)请你设计一个外墙根部两点A、B之间的距离,在(2)上画图,并说明理由．

点评:这道题体现了以下的转化思想:第(1)问转化为求对顶角或邻补角等;第(2)问是实际问题转化为构建两个全等三角形,转化为全等三角形的性质解决.

(三)数与形的转化

著名的数学家华罗庚教授曾在一首诗中写道:数形结合百般好,两家分离万事休.这一句话道出了数形结合这一方法的重要性.

例4:乘法公式的探究及应用.

(1)如左图,可以求出阴影部分的面积是____(写成两数平方差的形式);

(2)如右图,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是___,长是___,面积是___(写成多项式乘法的形式)

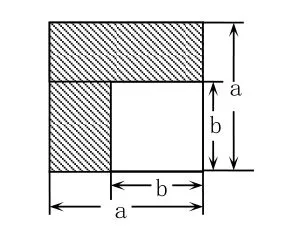
图5

图6

(3)比较左、右两图的阴影部分面积,可以得到乘法公式(用式子表达).

(4)运用你所得到的公式,计算下列各题:

①10.3×9.7②(2m+n−p)(2m−n+p)

点评:此题主要考查了平方差公式．即两个数的和与这两个数的差的积等于这两个数的平方差,这个公式就叫做平方差公式．对于有图形的题同学们注意利用数与形的相互转化求解更形象直观．

(四)实际问题与数学模型之间的转化

曹冲称象的故事中,聪明的曹冲知道大象的体重不能直接去称,就把称大象的重量转化为称石头的重量:他先把大象赶到船上,得到船吃水的深度;再把大象赶下船,往船上装一块块的石头,达到相同的吃水深度,于是,称出石头的重量即可得到大象的重量.曹冲的思维方法是实际问题与数学模型之间的转化.

例5:如图所示,在△ABC中,∠B=90°,AB=6厘米,BC=3厘米,点P从点A开始沿AB边向B以2厘米/秒的速度移动,点Q从点B开始沿BC边向点C以1厘米/秒的速度移动,如果P、Q分别从A、B同时出发,几秒钟后P、Q间的距离等于厘米?(把实际问题转化为几何问题)

图7

点评: 本题把实际问题转化为几何问题的数学模型,即转化为直角三角形中勾股定理的运用,本题中抓住BP=2BQ并且根据勾股定理求t是解题的关键.

四、结语

化归思想方法的主要特点是它的灵活性和多样性,是中学数学解题的重要思想方法,但并非万能的方法,即并不是所有的问题都可以通过化归而得到.解决的一个数学问题,组成主要元素之间的相互依存和相互联系的形式是可变的,其形式并非唯一,而是多种多样.所以应用数学变换的方法去解决有关数学问题时,就没有一个统一的模式可以遵循.因此,我们必须根据问题本身提供的信息,以“数学发现”为前提,利用动态的思维,具体问题具体分析,有创新的精神,不断地进行新的研究,在研究中获得新方法、新理论,去寻求有利于问题解决的化归途径和方法.

*注:本文是由董磊老师主持的广东省教育科学“十二•五”规划2011年度立项课题《如何在初中数学教学中滲透数学思想方法的实践研究》(课题批准号:2011TJK014)的研究成果之一.