一道中考题的解法分析与教学思考

厦门市海沧中学(361028) 蓝文英

一道中考题的解法分析与教学思考

厦门市海沧中学(361028) 蓝文英

1 试题呈现

(厦门卷第 25题)如图,在平面直角坐标系xOy中,已知 点A(1,m+1),B(a,m+ 1),C(3,m+3),D(1,m+a),m＞0,1＜a＜3,点P(n−m,n)是四边形ABCD内的一点,且△PAD与△PBC的面积相等,求n−m的值．

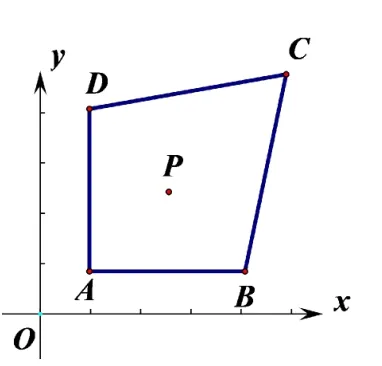
图1

2 优点解读

2.1 能力立意,数形结合

本题立足能力,涵盖知识点多,综合性强,具有较高的思维含量,考察学生的观察能力和基本经验与技能.以图形为载体,要求学生有较强的数感,能够借助图形,透过现象看本质,利用几何直观进行知识迁移.既检测学生的推理判断能力,又考查数学的数形结合与转化思想,试题具有很深的立意与延展性功能.

2.2 图形简洁,凸显思维

本题以四边形为背景,文字简约,图形简洁,但却蕴含着数学的核心思维.能否通过四边形四个顶点的坐标建立四边形边与边、边与坐标轴以及点P与四边形的顶点、边、对角线的联系,能否借助面积相等构造方程模型,能否通过几何直观、空间想象、图形变换联想筝形ABCD是轴对称图形而AC恰巧是对称轴,能否通过辅助线的添加探索点P的位置,能否透过验证发现点P在直线AC上,建立函数模型.这无疑对考生有较高的思维要求以及借助已有知识经验解决问题的能力.

2.3 形式创新,解法多样

在平面直角坐标系中研究图形变换是本题的一大特色,整个图形蕴藏着大量的数量关系,为学生解决问题提供了丰富的思维源泉.借助坐标系无疑打通了几何与代数的桥梁,由形推数,由数及形,相得益彰.从位置关系、图形关系的探究到数量关系的探究,从而衍生的解决问题的方法不仅多样而且新颖,精巧.一题多解、一法多用,丰富精彩的解法最终以不变应万变,充分发展学生的思维能力.

3 试题多解

结合图形分析题目条件,不难发现本题的突破口是应用数形结合思想及方程、函数思想,下面从“几何直观”这一核心素养建立不同的形与数的关系以及利用数形关系深入探析多种解法.

3.1 构建模型意识,立足常规解法

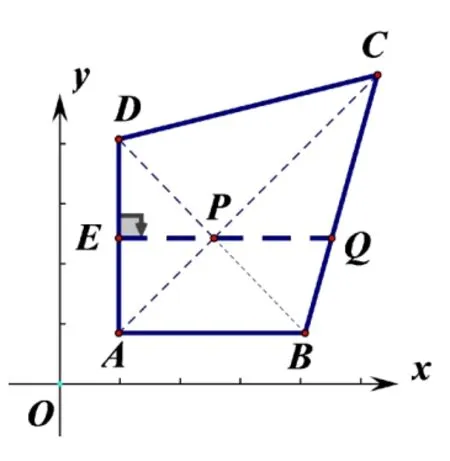
图2

解法1: 如图 2,过点P作PQ//AB交BC于点Q,延长QP交AD于点E,则依题意得PE⊥AD,∵A(1,m+ 1)、B(a,m+1)、C(3,m+3),D(1,m+a),P(n−m,m),m＞0,1＜a＜3,∴AB//x轴,AD//y轴,E(1,n),AB=AD=a−1,AB⊥AD,∴PE=n−m−1,∴

又∵S△PAD=S△PBC,∴①式和②式相等,比较分子即可.又∵1＜a＜3∴a−1/=0,∴−(n−m−3)=n−m−1.∴n−m=2.本法属于常规解法,借助三角形面积相等,构建方程以及函数模型,学生利用已有知识经验,立足通性通法,把未知量转化为已知量,充分考察学生的识图能力和数学的转化思想.

3.2 借助数学结合,搭数形数桥梁

妙法简析: 如图3,过点C作CF⊥AB交AB的延长线于点F,过点C作CE⊥AD交AD的延长线于点E,则CE=xC−xD=3−1=2,CF=yC−y−B=(m+3)−(m+1)=2,∴CE=CF,同理ED=BF=3−a,∴Rt△CDE～=Rt△CFB(SAS),从而CB=CD.又∵AB//x轴,AD//y轴,∴AB⊥AD,又∵A(1,m+1)B(a,m+1)、D(1,m+a),∴AB=AD=a−1.因此,四边形ABCD是轴对称图形,AC是对称轴,且AC是BD的垂直平分线.不难发现,四边形ABCD也是筝形ABCD.接下来,确定点P的位置,通过挖掘点P与顶点A、B、C、D的关联(即点坐标的特征),挖掘点P与四边形ABCD边的关联(即边的特征),挖掘点P与四边形对角线AC、BD的关联(即形的特征)可衍生三种巧妙解法.

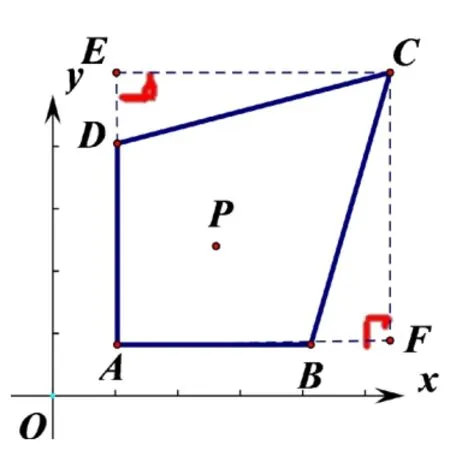
图3

解法2:如图4,∵A(1,m+ 1),C(3,m+3),P(n−m,m),观察发现这三点的坐标有个共同特点:纵坐标=横坐标+m,这就说明点P在直线AC上,并且直线AC的解析式为y=x+m(或利用待定系数法验证求得).又∵1＜a＜3∴a−1/=0,∴n−m−1=1,∴n−m=2.

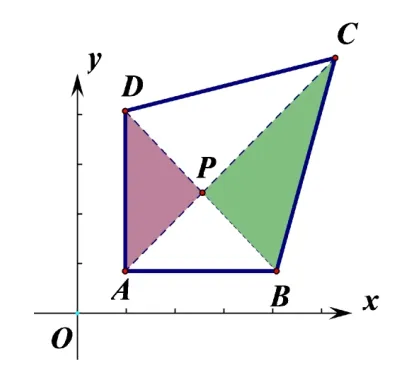
图4

解法3:如图5,过点P作PM⊥DA,PN⊥AB,垂足分别为点M和点N.∵P(n−m,m),∴点P到边AD的距离PM=−m−1,点P到边AB的距离PN=n−m−1,∴PM=PN,∴点P在的角∠DAB平分线上,即点P在对称轴AC上.由对称性进一步得到S△PAD=S△PAB,又由已知条件S△PAD=S△PBC,∴S△PAD=S△PAB=S△PBC=S△PDC,∴点P在AC的中点上.根据中点坐标公式:

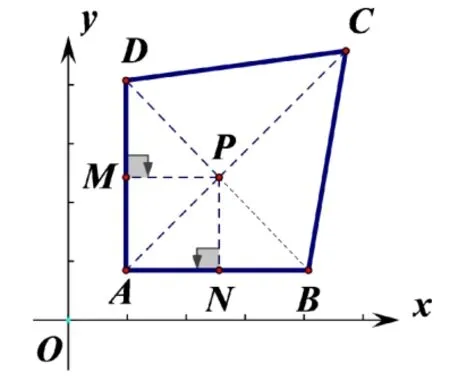
图5

解法4:如图5,观察点P与对角线的关联,点P是否在AC、BD上,进而转化为判定点P是否在直线上的函数问题.设直线AC的解析式为y=kx+b(k/=0),∵A(1,m+1)、C(3,m+3),根据待定系数法,求得直线AC的解析式为y=x+m,又∵P(n−m,m),显然点P的坐标满足直线AC的解析式为y=x+m,因此判定点P必然在AC上.故而,过点P作PM⊥DA,PN⊥AB,垂足分别为点M和点N.∵P(n−m,m),∴点P到边AD的距离PM=n−m−1,点P到边AB的距离PN=n−m−1,∴PM=PN=n−m−1,又∵AB=AD,同底等高所以有S△PAD=S△PAB,又由已知条件即

解法5:观察点P与对角线的关联,点P是否在AC、BD上,进而转化为判定点P是否在直线上的函数问题.设直线AC的解析式为y=kx+b(k/=0),∵A(1,m+1)、C(3,m+3),根据待定系数法,求得直线AC的解析式为y=x+m,又∵P(n−m,m),显然点P的坐标满足直线AC的解析式为y=x+m,因此判定点P必然在AC上.由于一三象限的角平分线为直线y=x,因为m＞0,将直线y=x向上平移m个单位就得到直线AC∶y=x+m,显然两条直线平行,因此AC平分∠DAB,无需作辅助线PM、PN.根据轴对称的性质和已知条件S△PAD=S△PBC,

解法2至5属于个性解法中的妙解,观察分析四边形ABCD顶点坐标的特点,从“点坐标的特征”探究出四边形“边的特征”,进而获得整个四边形“形的特征”,层层递进,思维螺旋上升.正如著名数学家徐利治教授所言:“几何直观是借助见到或者想到的几何图形的形象关系产生对数量关系的直觉感知.”即借助几何直观:“用坐标去还原图形,搭建形和数的桥梁”.以上巧解要求学生拥有较强的数感和空间观念、直观想象以及扎实的数学基本知识和基本经验,不同的切入点体现不同的思维层次,也充分体现命题者借助几何直观利用图形描述、理解和解决数学问题的考察意图.

4 教学思考

4.1 渗透几何直观,提高数学素养

著名数学家华罗庚是这样描述数和形的关系:“数形本是相倚依,焉能分作两边飞;数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”,真可谓一语中的.的确,解题的过程不仅是演绎推理的过程,更是发现和创造的过程,理性的逻辑分析固然重要,但那灵光一闪般的数感或直觉更加难能可贵.数感扎根于几何直观、基本经验、基本思想.一道题最容易想到什么,结合图形获得猜想,靠直觉或数感“识骨寻踪”,从而找到解决问题的突破口.在直观想象和空间观念的推动下,经历观察、猜想、探究、验证,思维呈梯度上升,直击问题核心.比如本题就是看到四边形ABCD的形状立马联想到边AB=AD、CD=CB,进而验证发现四边形ABCD果然是轴对称图形,点P的位置确定则呼之欲出.因此,“直观想象后的理性分析”显得尤为重要,是直达学生最近发展区的最短路径,所以在实际教学中,教师应有意识的渗透几何直观,创造数学活动让学生个体亲身经历,在创造体会中积累数学经验,提高几何素养.

4.2 突破思维僵局,触及几何本质

盲目的“刷题”无疑会阻碍学生思维的发展,只有建立在多角度、多方位、多元化思维的基础上的“触类旁通式”解题才能激发学生浓厚的学习兴趣,并促进思维更深层次发展.一题多解、一题多变、一法多用正是几何题的魅力.无论是自然解法还是个性解法,都立足于扎实的几何基本知识与识图能力.本题就是一个很好的诠释,比如观察四边形ABCD顶点的坐标的特点,得到AB//x轴,AD//y轴并且AB=AD;而观察C、B、D三点的坐标,通过不规则四边形补形为正方形或作垂直构造Rt△、证全等得到CD=CB,进而获得“四边形边的特征”,这便是解这道题的基石.在直角坐标系中研究图形的数量特征,用坐标还原图形,如果解法1是常规解法,那么解法2至5则开始打破常规思维,不仅思考问题的角度多元化,思维更是得到发散与延展.因此,教师在平时的解题教学中,不仅要引导学生开阔思路,强化几何直观意识,积累基本经验和技能,拔高思维层次,实现解题最优化.

5 结语

几何直观是《义务教育数学课程标准》(2011年版)提出的一个核心概念,它是借助图形和空间观念描述与分析问题的辅助手段,可以使复杂的数学问题简单化,是代表图形与几何的核心素养.与知识技能的学习不同,它是通过学生在不断解决问题的过程中慢慢“感悟与滋养”而来.因此,教师在实际教学中,需要为学生提供一片沃土让其生根、发芽.

[1]义务教育数学课程标准修订组.义乌教育数学课程标准(2011年版)解读[M].北京:北京师范大学出版社,2012

[2]章建跃,薛彬.义务教育教科书.数学(八年级下册)[M].人民教育出版社,2015

[3]王忠刚,王志进.一题多法的产生力求自然[J].中学数学教学参考:中旬,2016(3):40-41

[4]黄祥勇,荣彬.基于“直观想像”核心素养的教学启示[J].中学数学教学参考:中旬,2016(9):55-58