两种竖式计算形式带来的思考——小学低段数学算法选择策略的实践与研究

王 颖

在连加的竖式计算教学中怎样列竖式是我们教学的一个重点。不同的列式方式对学生的计算思想、计算能力会产生怎样的影响？为了更好地研究这个问题，笔者在课堂上有意识地记录了一个班在学习《连加》这一课前对连加竖式的尝试情况。主要有以下4种写法：

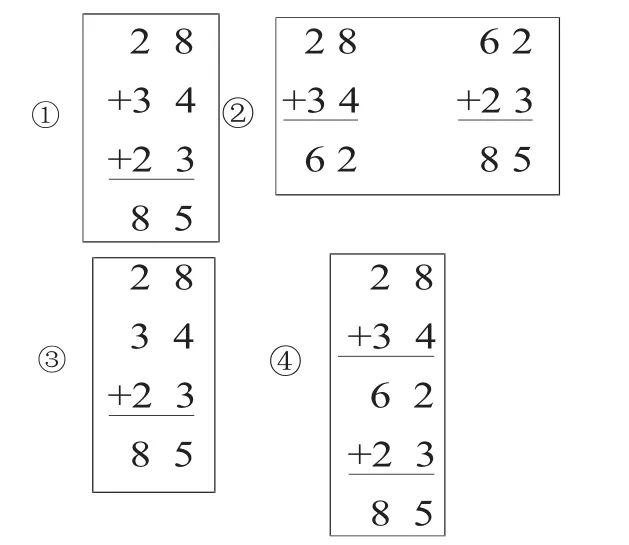
在过去的教学中，我们对第三、四种竖式形式有误解，即三个数叠加速度更快但容易错，而两个竖式连写则正好相反。为调查实际情况笔者做了一个小测试：用竖式计算23+30+29、45+28+19、27+12+34、37+11+23这四道题。为了体现测试所用数据一样、学生一样，笔者将全班44名学生分成了两部分，一半用三个数叠加形式计算，另一半用两个竖式连写形式计算，4个小时后，将算式顺序打乱，学生计算形式交换。测试结果为：在5分钟内完成的学生中，叠加形式的有30人，连写形式的有23人；在6分钟内完成的学生中，叠加形式的有39人，连写形式的有40人。从该数据可以看出：1.计算能力强的学生用叠加形式速度会更快；2.计算能力稍弱的学生更适合掌握连写形式；3.从完成度来看，连写和叠加形式相对均衡。再看正确率，从测试结果发现两种竖式形式并无明显差异，但错误的方式有所不同：叠加在较大的3个数字连加时易算错，而连写的错误主要集中在第一步。测试中有两名学生把算式的第二加数加了两次，这里也是学生需要注意之处。

那么，针对这些情况该怎样更好地处理教学活动？两种形式都在课堂上呈现，那么还是否需要对计算方式进行选择？笔者认为答案是肯定的，因为算法选择是算法多样化的最终归宿，但在两种计算方式既是基本算法，又都有优势的情况下，我们又该怎样选择？

一、对比感受，学会选择方法

学生往往认为自己的算法是最好的。如何让学生在切实感受的基础上选择出最合适的算法需要一个过程，更需要教师合理的总体设计与精心的课堂引导。

例如，在教学《连加》时，教师请学生尝试解决并在巡视中发现了以上四种笔算的形式，在对第一种竖式纠正后，教师将三种正确写法展示在黑板上。随后，请学生选出一种较好的方法并说明理由。学生通过观察、思考认为第二种方法太繁琐，而第三种、四种算法则各有其拥护者。这时教师并没有马上下结论，而是请学生分别用第三、四种方法计算23+40+16。计算后学生纷纷表示第三种方法更简便，这时教师又请学生分别用第三、四种方法计算29+38+26。这次学生们都认为用第四种方法更为简便，此时教师抛出问题：为什么你们会有不同的结果呢？学生思考后得出：不同算式适用的方法也不同，23+40+16由于个位中有0且数字较小，因此用叠加的方法比较简便，而29+38+26个位数字较大，用连写的方法计算更容易。

学生通过这样的对比过程都能从中充分感受、思考和经历一个由多样化到优化的选择过程，并进一步体会到算法选择并不是算法唯一化，实际上在连加计算中两种竖式都是很好的计算方式，选择用哪一个是由算式本身的具体数据而定的。

二、灵活思考，锻炼数学思维

数学是一种思维工具，数学思维具有逻辑的严谨性、高度的抽象性和概括性、丰富的直觉与想象等特征。这种思维特征能较好地锤炼学生思维能力、凸显学习个性。教师在平时的教学中，应加强学生科学抽象能力、逻辑推理能力和辩证思维能力的训练与培养，使学生在当今和未来的社会中，面对纷繁复杂的信息能作出正确的选择与判断，为其终生可持续发展奠定基础。

例如，当讨论“三个数叠加会出现满二十要向前一位进二”这一现象时，教师追问：有可能会满三十进三吗？

学生思考后回答：不可能。

师：为什么呢？

生：个位最大为9，三个数相加个位不可能超过三十。

教师继续问：那么四个数相加，个位最多满几十？为什么？

生:四个数相加个位最多满三十，因为个位最大只能是9，4个9相加也只有36。

又如，在讨论“什么情况下用三个数叠加竖式比较简便？”时，有学生这样回答：

生：三个数中个位有0时，叠起来算比较简便。

生：三个数中其中两个数的个位能凑成十时，也较简便。

生:三个数的个位很小，加起来不用进位也比较简便。

思考是智力的门户，是思维的前哨，是启动思维的按钮。思考的深刻与否，决定着创造性思维能否形成。教师自己对教学的内容应该有深入的理解，学生在学会思考之前，教师首先要学会思考，并理解每个数学素材的内涵。

三、启发思考，引导方法整合

由于学生对多种算法的不同思考角度缺乏认识，大多数学生会表现出对算法的点状思考和盲从，所以教师要注意引导学生学会类比思考，使学生在思考算法过程中对“何为相同角度、何为不同角度”进行感受和体验，从而选择出最适合某一学习内容的方法。

例如，对于28+34+23这道两位数连加题，教师将收集到的竖式方法写在黑板上，提问学生算法。

生：先算 28+34=62，再算62+23=85。

师：计算时要注意什么？

生：第一步满十要进一，第二步不用进一。

生：先算 28+34=62，再算62+23=85。

师：和第一种方法是一样的吗？

生：差不多，但竖式少写了一个62，更简便了。

生：我先算8+4+3=15，写5满十进一，再算2+3+2+1=8，最后等于85。

师：你认为在计算连加竖式时要特别注意什么？

生：注意满十进一。

生：注意满几十就要进几。

这样教学，通过对不同算法之间本质联系的揭示，将散点的多种方法经过提炼抽象，从而使学生的思维从具体向抽象提升。

四、依据需要，建立选择意识

计算教学不仅是学生对算法的掌握，更重要的是以计算教学为载体，帮助学生建立判断与选择的自觉意识，养成从实际需要出发选择适合计算方式的学习习惯。在教学中，我们可以从两方面来唤醒学生的判断与选择意识，一是学会根据自己的状况作出判断与选择，二是学会根据具体情境的需要作出判断与选择。

例如，在《连加》教学中，学生发现不同的连加竖式适用于不同的具体算式。而在连减计算中学生感受到三个数叠加的形式很难进行，尤其是要连续退位时，这时选择两个竖式连写是更为合适的方法。而当学生学习加减混合计算时就会更有体会，三个数叠加竖式无法计算加减混合运算，只能选择两个竖式连写的方式。可见优化与选择有时候并不是一堂课就能够解决的，它需要合适的状况、具体的情境。

通过这样的学习，学生能够从过程中真正感受到不同的计算方式适合其相应的具体情境和数据，对数字更加敏感，在方法的选择上意识也会更强。

（本文作者系朱乐平数学名师工作站“一课研究”组成员）