非刚性轴承润滑与变形耦合下的轴系校中研究

蒋 平，朱汉华，严新平，朱军超

（武汉理工大学 能源与动力工程学院，武汉 430063）

非刚性轴承润滑与变形耦合下的轴系校中研究

蒋 平，朱汉华，严新平，朱军超

（武汉理工大学 能源与动力工程学院，武汉 430063）

轴承油膜是影响轴系校中的动态因素之一。在油膜刚度的计算过程中，较多学者采用船级社推荐值，或将轴承考虑为刚性，利用差分法或有限元法对其进行求解。文章对轴承弹性变形与油膜压力进行耦合分析，获得最优小扰动量，得到更符合实际情况的油膜刚度，利用vb.net编写有限元轴系校中软件并对某油船轴系进行校中计算，分析了轴承油膜对轴系校中的影响程度，可为船舶轴系校中计算及检验提供参考。

轴系校中；有限元法；油膜刚度；vb.net

0 引 言

轴系是船舶的重要组成部分，其安装的好坏与否直接影响船舶的运行状态。轴系校中常使用的方法主要有：传递矩阵法、三弯矩法和有限元法。在上世纪九十年代，由于计算机运行速度不高，传递矩阵法成为当时最流行的方法，许多学者应用该方法进行分析讨论[1]。大连海事大学的魏海军[1]将艉轴多支承、油膜刚度利用传递矩阵法一一进行分析。在本世纪初，周瑞平[2]对三弯矩法进行了改进，加入了影响轴系校中的多个因素，提高了三弯矩校中的准确性。随着计算机的高速发展，有限元法计算速度和精度得到巨大的提升，大连理工大学的曹学涛和刘玉君等[3]利用商用有限元软件对轴系进行了校中分析，认为该方法的计算结果具有很高的精度，且计算时间也不是很长。

之前，许多船级社和学者对轴系校中的影响因素进行了大量研究。DNV船级社在校中计算中考虑了轴承支座的热变形，同时也在着手研究船体、支承变形和螺旋桨水动力对轴系校中的影响[4]。中国船级社提出了在校中计算时需要考虑齿轮箱中的齿轮啮合力影响[5]。波兰船舶研究中心的Lech Murawski将船体刚度、轴承刚度、油膜刚度进行耦合，分析刚度对轴承反力的影响[6]。荷兰的Machine Support公司在其轴系设计软件ShaftDesigner的轴系校中模块中加入了后艉轴承水力润滑的影响。

随着船舶的巨型化发展，油膜润滑对轴系校中的影响愈显突出。DNV船级社在校中计算中给出油膜刚度推荐值。荷兰Machine Support公司在其船舶推进轴系设计软件Shaft Designer中将水力润滑与接触应力进行耦合分析，获得了更符合实际的应力分布图。武汉理工大学的周瑞平利用有限差分法求解了轴承刚度。江南造船集团公司的耿厚才利用数值计算方法获取了油膜的刚度与阻尼并计算了弹性支承下的轴承反力。

1 轴系校中有限元法

1.1 坐标系的建立

以轴系螺旋桨末端为坐标原点，轴系理论中心线为x轴，正向指向船艏，过原点垂直x轴向上为z轴正向；根据右手法则，y轴方向为垂直纸面向内。P为集中载荷，q为均布载荷，Zb为轴承变位，θ为轴截面转角，Q为轴截面剪力，M为弯距，m为外加力偶，R为轴承支反力。一般取与z轴同向为正，顺时针方向为正，其中轴承位移一般取相对轴系理论中心线向下为正，向上为负。

1.2 有限元刚度矩阵

在推导船舶轴系单元刚度矩阵的时候，将单元看作为一段梁单元，利用势能法、伽辽金法均可得到梁单元的刚度矩阵。在国内外的很多著作中[7]，都对其进行了详细的推导，故本文就不再进行推导，只给出最终结果。轴系单元刚度矩阵可以表示如下：

式中：E为单元材料的弹性模量，船舶轴系材料E一般取2.06×1011Pa；I为单元对z轴的惯性矩；L为单元的长度。

在获得了各个轴段单元刚度矩阵后，将这些刚度矩阵按一定规则进行处理，使其组成一个总的刚度矩阵K。

1.3 外部载荷的处理

由轴系校中所建立的模型发现，作用于轴系上的外部载荷分为均布载荷和集中载荷两大类。集中载荷作用于轴系节点上，可以直接作为载荷向量分量；而均布载荷平均分布于轴段上，需要进行等值节点力的转换才可以进行下一步的计算。根据结构力学的相关知识，对均布载荷进行等效节点力的转换，使其能够产生相同的效果：作用于长为L轴段上的均布载荷q等效于分别作用于轴段两端的集中力qL/2和弯矩qL2/12。

1.4 约束条件的设置

船舶轴系校中最终是要将轴系敷设成某种曲线状态。因此在校中计算过程中，需要对轴承位移进行修改。在有限元校中方法中，对轴系支承位移进行修改主要有两种方法：置大数法、置换法。置大数法是一种近似计算的方法，其计算精度没有置换法高；另一方面，置大数法由于需要将整体刚度矩阵中的某一值乘上一个足够大的数，从而导致该刚度矩阵的模在Matlab中显示为无穷大，进而无法进行求逆运算，作者通过在Matlab中验证发现某些刚度矩阵无法通过置大数法进行求解。

船舶轴系整根轴受力与变形关系：

式中：δ=［δ1,δ2,…δ2n］T；F=［F1,F2,…F2n］T

式中：K整个结构（轴系）的刚度矩阵；δ为作用于每个节点上的线位移和角位移；F为作用于每个节点上的集中力和弯矩；n为所划分节点个数。

将（2）式展开，代入边界条件并进行相关变换后可得：

式中：k为轴系刚度矩阵中的各个元素；δ为作用于每个节点上的线位移和角位移；F为作用于每个节点上的集中力和弯矩；b为第r处节点所产生的轴承变位。

通过（3）式变换，当有轴承变位时，只有载荷量发生变化，而系统的刚度矩阵没有任何改变，可以达到简化计算的效果。置换法是一种通用的处理方法，不管单元刚度矩阵如何变化，只要结构的几何构造正确，集成总体刚度矩阵之后总是可以通过置换法使得总体刚度矩阵为非奇异，同时这种方法也存在编程繁琐的弊端。

2 轴承润滑与变形耦合基本原理

2.1 雷诺方程及其求解[8]

稳定运转的向心滑动轴承雷诺二维方程：

式中：h为径向油膜厚度；U为轴颈线速度；p为油膜分布压力。

式中：r为轴颈半径；d为轴颈直径；L为轴承长度；Cr为轴承半径间隙；λ，φ为轴承轴向和圆周方向无量纲坐标，）；H为无量纲油膜厚度；P为无量纲油膜压力。

本文分析对象为稳定运转的向心滑动轴承，其油膜厚度是稳定不变的，故在对（5）式进行差分迭代计算之前可给出油膜的厚度方程，将此方程无量纲处理后可得[9]：

式中：ε为各个截面上的轴颈偏心率，φ为偏位角。

将油膜离散为长方形网格，行列分别表示圆周方向和轴向方向，将偏微分方程离散为代数式形式，进而将各节点油膜压力用已知量进行表示，再加入各个边界条件，便可对其进行求解，通过反复迭代，便可得到满足精度要求的油膜压力分布。编程思路如图1所示。

本文在进行雷诺方程求解的时候，为了提高计算精度，同时加快计算速度，在对求解区域离散时采用了半步长插入形式；在进行迭代求解时，采用了超松弛算法（SOR）。

2.3 轴承润滑与变形的耦合[10，13-14]

为了能够达到将轴承弹性变形与油膜压力两者进行耦合分析的目的，在对轴承变形进行计算时，采用了有限元的思想。

对求解区域 （轴承内表面）划分网格，网格大小与形式保持与上述求解油膜压力分布时所划分的网格一致。在获得了油膜各个节点压力后，将这些压力以外部载荷形式作用于已进行了有限元网格划分的轴承各节点上，加入符合实际的约束，进行有限元求解获得相应的轴承表面位移变化Δh。将此Δh叠加到最初油膜厚度中，再次进行雷诺方程求解，以此不断循环，直至达到相应精度。编程思路如图2所示。

2.4 油膜刚度计算算例

根据上述方法，对一艘油船后艉轴承油膜进行了计算，该船后艉轴承主要参数如下：轴承宽1 180 mm，轴颈外径548 mm，轴承半径间隙0.5 mm，轴颈偏心距0.23mm。采用Matlab软件处理可获得未考虑轴承变形油膜压力分布图、考虑轴承变形油膜压力分布图以及考虑轴承变形轴承内表面变形图。

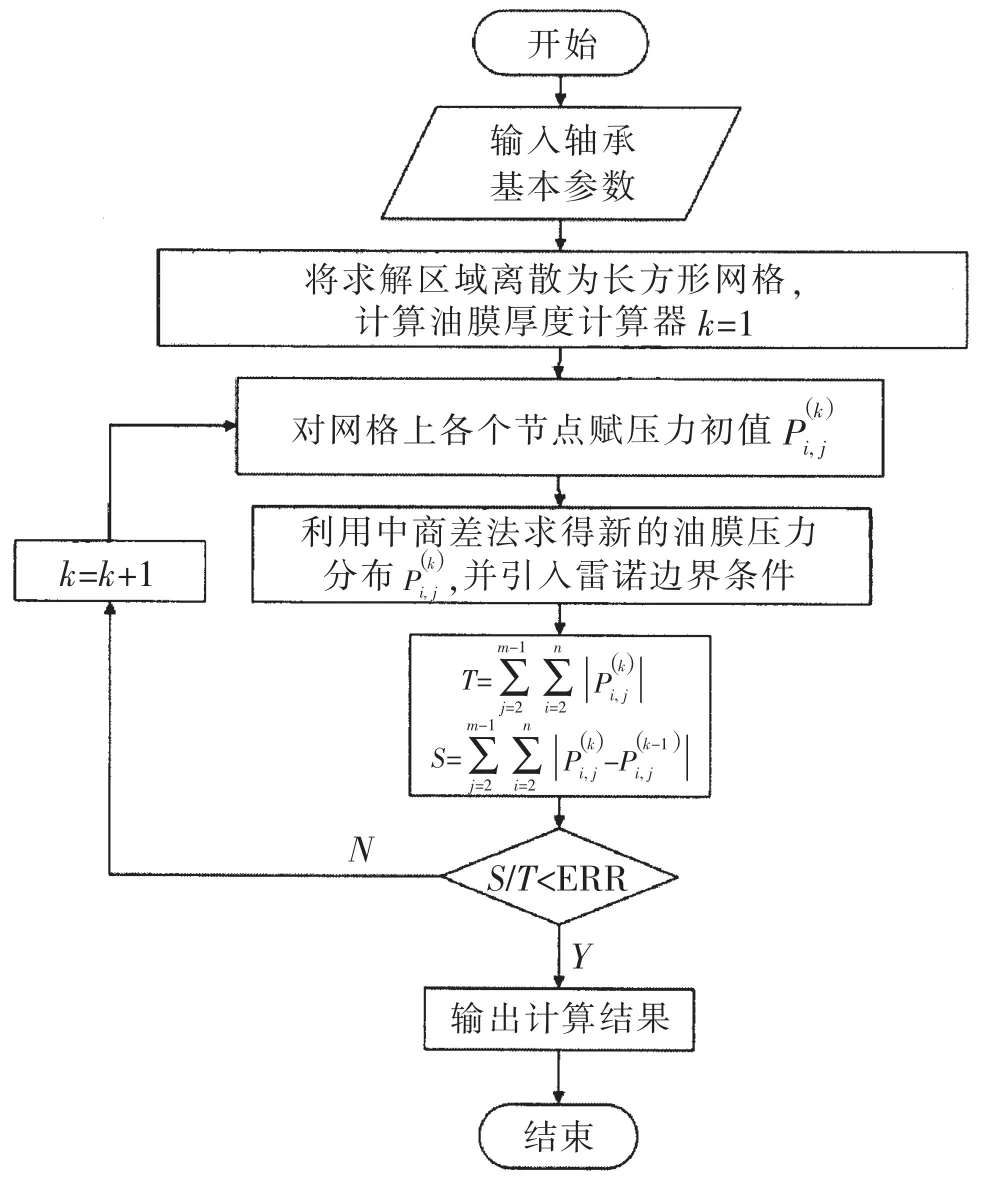
图1 雷诺方程求解Fig.1 Solution of Reynold’s equation

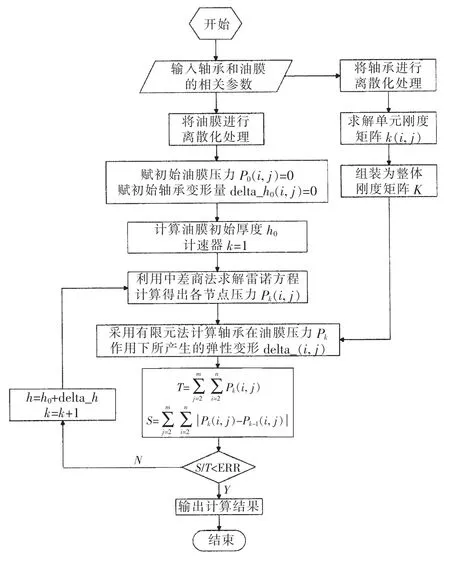
图2 轴承变形与润滑耦合分析Fig.2 Analysis of coupling bearing deformation with lubrication

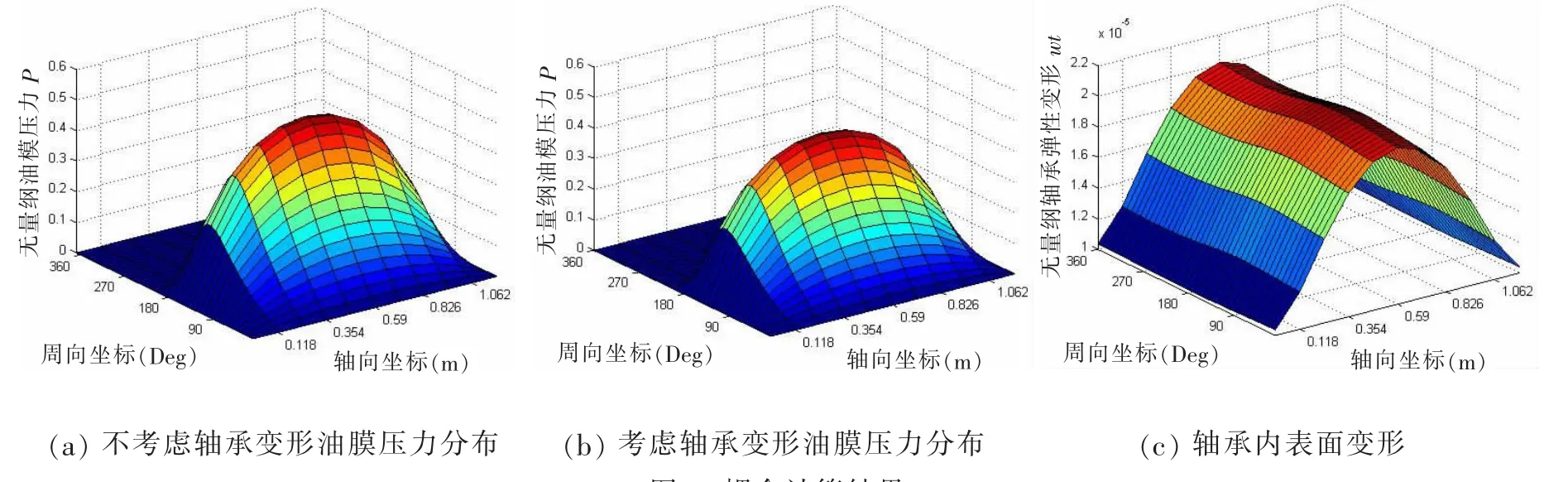
图3 耦合计算结果Fig.3 Results of coupling calculation

在Matlab中调用已编制的m文件，可以获得不考虑轴承变形与考虑轴承变形这两种情况下的无量纲油膜压力峰值、无量纲最小油膜厚度以及计算所耗的时间，具体数值如表1所示。

表1 不同因素下的油膜参数Tab.1 Oil film parameters under different factors

由表1可以看出：在考虑了轴承的弹性变形之后，油膜压力明显变小；由于轴承产生弹性变形，导致了最小油膜厚度变大；本文在求解中发现考虑轴承弹性变形的计算时间远远大于不考虑轴承变形的计算时间，这主要是因为计算中需要进行六面体八节点单元的刚度矩阵计算与组装，而这一过程需要大量计算时间。

在进行计入油膜影响的船舶轴系校中计算前，需要计算出油膜的平均刚度，而油膜刚度的计算分为差分法和有限元法两种。在利用差分法进行油膜刚度计算时，小扰动量的选择决定着油膜刚度的正确与否。本文中在1×10-1mm～1×10-10mm之间平均选取10个小扰动量，计算了在不同扰动量下的油膜平均刚度。

由表2可以看出，随着小扰动量Δy逐渐变小，润滑油的油膜刚度也逐渐变小，当小扰动量小到某一数值时，润滑油的油膜刚度将基本不再变化，认为此时的小扰动量为最佳值，可以利用该值来求解油膜刚度。本文中，认为最佳小扰动量Δy为1×10-5mm。较不考虑轴承弹性变形，在考虑了轴承弹性变形之后的油膜刚度比前者略大。在本文的校中计算中，取考虑了轴承变形的油膜刚度2.196 450×108N/m。

3 实船分析

根据有限元轴系校中原理，作者利用vb.net编制了轴系校中软件，软件主要输入数据有：各个轴段的密度、浮力系数、外径及内径等。主要输出数据为：直线校中结果、轴承影响系数、合理校中结果等。

本文以一艘油船轴系为例，利用自编的有限元轴系校中软件进行了计算，将油船数据输入后，可以直接在输出文件中得到轴承的影响系数如表3所示。

在计及油膜影响时，引入上述2.3中的油膜刚度计算方法，利用有限元的校中方法，计算了油膜影响下的各个轴承的负荷情况。

由表4可以看出：考虑了弹性轴承的润滑影响之后，轴系合理校中的各个轴承负荷与不考虑任何影响因素的轴承负荷相比分别变化了-9.074%、2.983%、-6.787%、2.096%和-1.746%。可见，当轴承负荷较大时，油膜厚度减小，相当于作用在轴系上的等效轴承变位减小，使得轴承负荷相应地减小；反之亦然。在轴系校中中，计入油膜影响后，增加了轴系的柔度，从而实现了轴系通过自身对轴承负荷进行均匀调配，保证了轴系的安全性与稳定性。

4 结 论

（1）在本文油膜刚度计算过程中，将油膜压力与轴承变形耦合分析并取小扰动量为1×10-5mm可以获得更接近实际情况的油膜刚度。油膜刚度值一般保留三位有效数字即可满足轴系校中计算的要求，而通过其他算例的计算发现，一般取小扰动量为1×10-5mm可以保证刚度精确到三位有效数字。

（2）在油膜润滑计算中，将轴承弹性变形与油膜润滑进行耦合分析。即将有限元法与差分法进行组合，采用耦合问题的方法进行求解，计算结果更符合实际情况。该方法具有计算精度高，结果更合理的优点，但是计算时间较长。

（3）在轴系校中中，计入轴承润滑油膜影响后，实现了轴系通过自身对轴承负荷进行均匀的调配，保证了轴系校中安全性与稳定性。

[1]魏海军,王宏志.船舶轴系校中多支承问题研究[J].船舶力学,2001,5(1):49-54. Wei Haijun,Wang Hongzhi.Study on multi-bearings of shipping shaft system alignment[J].Journal of Ship Mechanics, 2001,5(1):49-54.

[2]周瑞平.超大型船舶推进轴系校中理论研究[D].武汉:武汉理工大学,2005. Zhou Ruiping.The theoretic studies on the propulsion shafting alignment of ultra-large vessels[D].Wuhan:Wuhan University of Technology,2005.

[3]曹学涛,刘玉君,李艳君,邓艳萍.基于ANSYS的船舶轴系校中的双向优化研究[J].造船技术,2009,289(3):11-15. Cao Xuetao,Liu Yujun,Li Yanjun,et al.Research onmutual optimization of shafting alignment based on ANSYS[J].Marine Technology,2009,289(3):11-15.

[4]陆金铭,周海港,顾卫俊,马 捷.船舶轴系动态校中轴承油膜的影响计算[J].船舶工程,2009,31(6):69-72. Lu Jinming,Zhou Haigang,Gu Weijun,et al.Calculation of the influences ofmarine shafting dynamic alignment affected by bearing oil film[J].Ship Engineering,2009,31(6):69-72.

[5]中国船级社.船上振动控制指南[S].2011.

[6]Lech Murawski.Shaft line alignment analysis taking ship construction flexibility and deformation into consideration[J].Marine Structures,2005,18(1):62-84.

[7]Daryl Logan.有限元方法基础教程[M].北京:电子工业出版社,2003.

[8]朱汉华,刘焰明,刘正林,等.船舶艉轴承变形对其承载能力影响的理论及试验研究[J].润滑与密封,2007,32(6):12-14. Zhu Hanhua,Liu Yanming,Liu Zhenglin,et al.Theoretic and experimental research on the influence of ship stem bearing deformation to its carrying capacity[J].Lubrication Engineering,2007,32(6):12-14.

[9]刘正林,周建辉,刘 宇,陈汝刚.计入艉轴倾角的船舶艉轴承液膜压力分布计算[J].武汉理工大学学报,2009,31 (9):111-113. Liu Zhenglin,Zhou Jianhui,Liu Yu,et al.Compution on pressure distribution of stern bearing liquid film reckoning in inclination of stern shaft[J].Journal ofWuhan University of Technology,2009,31(9):111-113.

[10]de Kraker A,van Ostayen Ron A J,Rixen D J.Calculation of stribeck curves for(water)lubricated journal bearings[J]. Tribology Internartional,2007,40(3):459-469.

[11]Class N K.Guidelines on shafting alignment[K].2006.

[12]SchifferW.Advancedmethods for static and dynamic shafting caculation[J].Brodogradnja,2007,58(2):158-164.

[13]刘志峰,湛承鹏,赵永胜,李小燕,夏龙飞,马建川.倾斜状态下静压油垫承载性能研究[J].工程力学,2015,32(5): 208-212. Liu Zhifeng,Zhan Chengpeng,Zhao Yongsheng,Li Xiaoyan,Xia Longfei,Ma Jianchuan.Research on the bearing performance of hydrostatic oil pad under tilting condition[J].Engineering Mechanics,2015,32(5):208-212.

[14]Ropars P,Desceliers C.Amodal strategy devoted to the hidden state variablesmethod with large interfaces[J].ComputationalMechanics,2015,55(5):1-14.

Research on bearing lubrication and deformation on shafting alignment

JIANG Ping,ZHU Han-hua,YAN Xin-ping,ZHU Jun-chao
(Energy and Power Engineering,Wuhan University of Technology,Wuhan 430063,China)

In the research of the influence of shafting alignment,rigidity of bearing oil film is one of the dynamic factors.In the calculation of rigidity of bearing oil film,most researchers used the recommended value of Classification Society or considered the bearings as rigid to solve by the finite differencemethod or finite elementmethod.In this paper,the coupled analysis of the bearing elastic deformation and pressure of oil film is carred out,The best small disturbance and most realistic rigidity of bearing oil film are obtained.The shafting alignment program with Visual Basic is developed and the shafting of a tanker is calculated,which could provide reference to the calculation and survey of shaft alignment.

shaft alignment;finite elementmethod;oil film stiffness;vb.net

U664.21

：Adoi:10.3969/j.issn.1007-7294.2017.02.011

2016-09-23

国家自然科学基金重点项目（51139005）和校研究生创新基金（2012-zy-045）资助

蒋 平（1987-），男，硕士研究生，E-mail:jsczjp2000@163.com；朱汉华（1968-），男，教授，博士生导师。

1007-7294（2017）02-0211-07