关于在役舰艇非概率可靠性模型的安全性评估

滑 林，吴 梵，牟金磊，卢清亮

（海军工程大学 舰船工程系，武汉430033）

关于在役舰艇非概率可靠性模型的安全性评估

滑 林，吴 梵，牟金磊，卢清亮

（海军工程大学 舰船工程系，武汉430033）

文章基于非概率可靠性理论和概率统计理论，结合描述抽样的蒙特卡洛数值模拟法，建立了腐蚀损伤下的现役舰艇船体结构非概率可靠性和概率可靠性分析模型。然后，以某大型舰艇为例，采用两种可靠性分析模型对该舰腐蚀损伤后船体结构的可靠性进行了分析，最后，对两种可靠性分析模型的计算结果进行了对比。结果表明：非概率可靠性理论既凸显不确定性变量的客观随机性又兼具计算量小、效率高、结果保守等优势，在工程应用中具有较强的适用性和实用性。

在役舰艇；非概率可靠性；概率统计理论；蒙特卡洛数值模拟

0 引 言

船舶结构的可靠性是指船舶在规定的使用期限内，在设定的航行海况条件下船体结构保持安全状态的能力。随着数理统计理论的发展，船舶结构可靠性评估成为研究热点，国外学者Mansour[1]在基于概率理论的船舶的可靠性评估方面做了大量的工作，先后提出了船体波浪弯矩的短期和长期概率分布形式，计算了船舶在多种失效模式下的可靠度，并探讨了可靠性在船舶设计中的方法；Paik[2]分别采用中心安全因子和一阶二次矩法对双层底油船的可靠性和安全性进行了评估。国内学者冯国庆等[3]在考虑了材料的屈服极限和模型的不确定性后，建立了屈服强度可靠性分析的极限状态方程，提出了一种新的船体结构屈服强度可靠性分析方法。对于设计建造阶段的船舶，在计算机技术的推动下其结构可靠性评估方法得到了快速发展，相关理论和技术也已在工程中得到广泛应用。但对于现役船舶结构，由于不确定性变量的概率密度函数或隶属函数难以确定，造成传统可靠性计算方法在现役船舶结构可靠性评估中成本高、效率差，严重制约了其在现役舰艇船体结构安全性评估中的发展。近年来，随着舰艇老龄化及国家海洋战略的需要，现役舰艇船体结构的可靠性评估成为当前一个新研究热点。现役舰艇在服役过程中通常会遭受腐蚀、疲劳和变形等损伤的影响，这加剧了数据的采样难度，造成传统可靠性评估方法在现役舰艇结构中的实用性大幅减弱。一种实用性好、计算效率高和评估结果保守的可靠性评估方法亟待研究。

目前，非概率可靠性评估理论由于克服了对样本数据过度依赖在航空、土木工程等领域得到了较为广泛的应用。但在船舶工程领域方面，其可行性及计算分析结果的准确性尚不明确。鉴于此，本文基于非概率可靠性理论和概率统计理论，结合描述抽样的MCS模拟法，建立了腐蚀损伤下的现役舰艇船体结构非概率可靠性和随机概率的可靠性分析模型，对某大型舰艇船体结构可靠性进行分析，验证非概率可靠性理论在现役舰艇结构安全性评估上的可行性。

1 现役舰艇船体结构可靠性分析

1.1 船体结构抗力

在腐蚀损伤作用下，船体构件的厚度逐渐减小、变薄，导致了船体结构的抗力衰减。对于船体结构的腐蚀，秦圣平等[3]在综合了其他腐蚀模型的基础上，提出了一种拟合能力最好、适用性较强的一种模型。该模型认为船舶结构的腐蚀满足Weibull分布，构件腐蚀损伤的计算公式为：

式中：d（）T为T时间后构件的腐蚀厚度；Tst为腐蚀开始的时间；TL为结构的使用寿命或维修周期；dm为构件腐蚀的极限厚度；α、γ为计算系数。

舰艇在服役一定期限后，其计算剖面的剖面积A、静矩S以及剖面相对于中和轴的惯性矩I随时间的累积而减小，相应的计算公式为：

式中：bi为构件i的宽度；ti为构件i的建造厚度；hi为构件i距参考轴的垂直距离；φi为构件i与剖面中线的夹角。

腐蚀损伤后，计算剖面处的最小剖面模数Wmin为：

式中：S（T）为T时刻剖面静矩；A（T）为T时刻剖面积；I（T）为T时刻剖面相对于中和轴的惯性矩；hd为主甲板距参考轴的最大距离；hb为船底外板距参考轴的最大距离。

1.2 载荷效应

作用在船体的载荷主要是静水弯矩和波浪弯矩。由于静水弯矩的变化较小，美国船舶结构委员会（SSC）认为其服从正态分布，均值可取船级社规范允许最大静水弯矩Ms,max的60%。劳氏船级社给出了船舯剖面处最大静水弯矩Ms,max的计算公式[4]：

式中：L为船长；B为船宽；CB为方形系数；Cw为计算系数，其计算公式为：

舰艇承受的波浪载荷主要受其航行海况、航速及航向角的影响。统计资料表明：波浪载荷Mw的短期分布满足Rayleigh分布[5]，而长期分布则服从Weibull分布[6-7]，对应的概率密度函数f（Mw）及概率分布函数F（Mw）为：

对应的波浪载荷幅值的均值μMw和方差σMw分别为：

式中：Γ（）为Gamma函数；hw为形状参数；Mo为设计舰艇寿命周期内所遭遇的最大波导弯矩，其计算公式为[8]：

式中：Cw的计算方法见公式（5）。

1.3 船体结构的失效模式

在外载荷作用下，船体结构的失效模式主要有两种：中垂或中拱状态下，船体结构的屈曲；中垂或中拱状态下船体结构的屈服，即剖面中离中和轴最远纤维中的最大弯曲应力达到了屈服应力[9]。由于舰艇船舯剖面处中和轴靠近船底且中垂状态下的波浪载荷相对较大，所以常以中垂下甲板结构的屈曲作为舰艇可靠性分析时的主要失效模式[10]。对应的结构失效函数为：

式中：SR为船体结构抗力；κ为计算系数；σs为材料的屈服极限，其通常满足正态分布[11]。

2 现役舰艇船体结构可靠性分析模型

2.1 M onte Carlo数值模拟法

Monte Carlo数值模拟法（MCS）是可靠性分析中最基本的数值模拟方法。在实际工程中，由于其工作量庞大而没有被广泛应用。但在理论研究中，由于其较好的计算精度常作为标准方法来检验其他方法的可行性。MCS的基本原理为：将结构的不确定性因素表示为结构的随机变量X,Y,…,Z，在确定其概率分布的情况下，通过对X,Y,…,Z进行随机抽样确定结构响应M的数字特征（均值、方差和变异系数等），最后得到结构失效函数的概率密度函数f（x）。为了进一步提高MCS仿真精度，减小结果的标准误差，本文采用描述抽样的采样方法。其计算的流程，如图1所示。

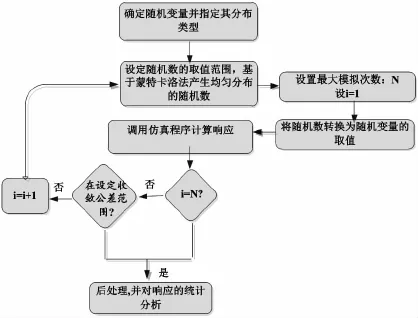
图1 MCS法计算流程图Fig.1 The calculation flowing chartofMCS

2.2 现役舰艇结构概率可靠性分析模型

设船体结构失效函数为G=（Wmin, σs,Ms,Mw）＝g（x1,x2,…xn）采用均值一次二阶矩法将其在随机变量的均值点 μx= （μx1,μx2,…μxn）处线性展开成泰勒级数，即：

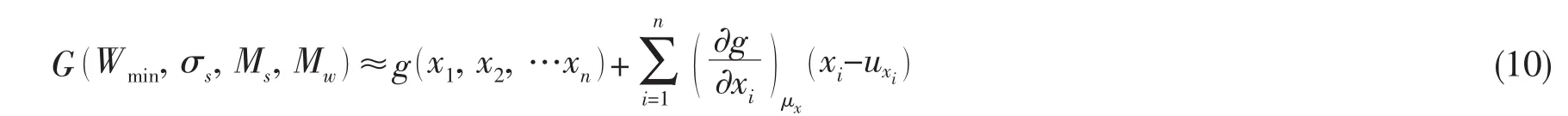
由（10）式可近似得到船体结构失效函数的均值μg和方差σ为：

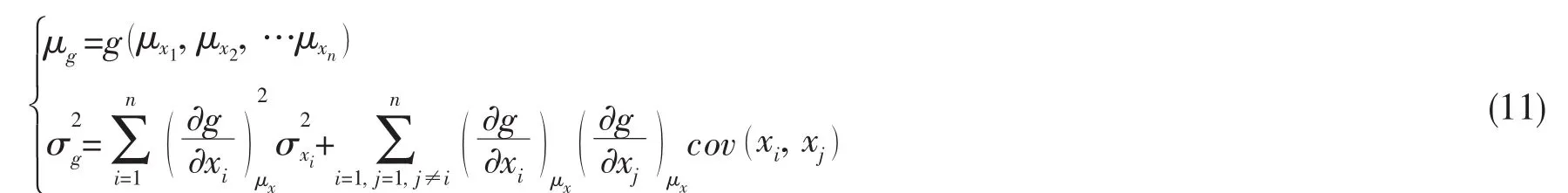
基于概率可靠性理论的安全指数β定义为：在标准化后的坐标系内，从原点到失效面的最短距离。对应的船体结构安全指数β对应的计算公式为：

针对舰艇船体结构可靠性评估，文献[10]规定：当采用第二水平法对舰艇结构进行可靠性分析时，若船体结构的安全指数β≥1.680，则认为舰艇结构处于安全、可靠的状态。

2.3 现役舰艇结构非概率可靠性分析模型

Ben-haim[12]采用凸集模型描述结构中“未确知但有界”的变量，以结构所能允许的不确定性的最大程度来衡量其可靠性，这就是“非概率可靠性”的基本思想。郭书祥[13]在区间模型的基础上，完善了该思想，提出了非概率可靠性分析理论。

对于现役舰艇，由于实际勘验中测得船体构件的腐蚀剩余厚度极其有限，有限的测点仅能确定其现时状态下变量的波动范围，而非概率可靠性理论将随机变量作为区间变量处理，这就使得基于非概率可靠性理论开展现役舰艇船体结构可靠性分析具备了初步的可行性。

设x∈XI=［Xl,Xu］为舰艇结构相关的区间变量，则区间变量的均值xc和离差xr为：

由区间变量组成的向量X=｛X1,X1,…,Xn｝表示与船体结构有关的基本区间变量的集合，其中xi∈X（ i=1,2,…,n ），由舰艇船体结构失效函数及区间数学理论可知，当g=（x1,x1,…,xn）为xi（ i=1,2,…,n）的连续函数时，G（ Wmin,σs,Ms,Mw）亦为区间变量，船体结构非概率可靠性指标为：

非概率可靠性指标η的几何意义为：将区间变量标准化后按无穷范数度量的从坐标原点到失效面g=（x1,x1,…,xn）的最短距离。n维曲面g=（x1,x2,…,xn）将船体结构的基本参量空间分为失效域和安全域两部分。η越大，结构性能的波动区域距失效域越远，结构越可靠、抗干扰性越强。当η＞1时，∀xi∈X（ i=1,2,…,n ），均有G（ Wmin,σs,Ms,Mw）＞0。此时，船体结构处于可靠状态；当η≤1时，∀xi∈X（i=1, 2,…,n），G（ Wmin,σs,Ms,Mw）既有可能大于0，也有可能小于0。此时，可认为船体结构处于不可靠状态。

3 算例及分析

以某大型水面舰艇为计算对象，由于船舯剖面是船舶结构中最为典型的计算剖面，故取其船舯剖面为计算剖面。已知该舰设计水线L为98.0 m；排水量Δ为1 457.26 T；设计水线宽B为10.2m；平均吃水Td为2.97m；设计波高Hs为5.27m；航速V为29 kns；方形系数CB为0.49。

由于船体结构抗力SR是船体构件厚度yi（构件的长度和宽度为定值）和材料屈服强度σs的函数，其函数形式为：

由（1）、（2）和（3）式可知，计算参数dm，Tst，γ，α等参数对船体结构抗力的影响较为显著。对于上述计算参数，文献[4]认为其均服从正态分布。本文在实船勘验数据的基础上，采用待定系数法初步确定了相关参数的平均值，并采用文献[4]给定的各参数的变异系数。各参数的数字特征，如表1所示。

表1 结构抗力参数数字特征Tab.1 The numerical characteristics of structural resistance

采用MCS法对现时状态下（服役10年）船体结构抗力SR进行103万次的数值模拟，得到其概率分布及累积概率分布图，通过回归分析还可得到概率密度函数曲线和分布函数曲线，如图2、3所示。

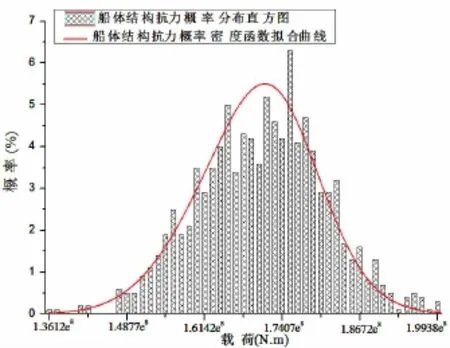
图2 结构抗力SR的概率分布Fig.2 The probability distribution of structural resistance SR

图3 结构抗力SR的累积概率分布Fig.3 The accumulative probability distribution of structural resistance SR

通过对图2、3所示的抗力SR的概率分布及累积概率分布图的统计特征值进行分析，可得现时状态下舰艇船体结构抗力的数字特征及其波动范围，具体数据如表2所示。

表2 舰艇现时状态下结构抗力的数字特征Tab.2 The numerical characteristics of warship structural resistance under the current state

对静水弯矩和波浪弯矩进行103万次的MCS模拟，得到舰艇静水弯矩和波浪弯矩的概率分布和累积概率分布图及相应的概率密度函数曲线和分布函数曲线，如图4、5所示。

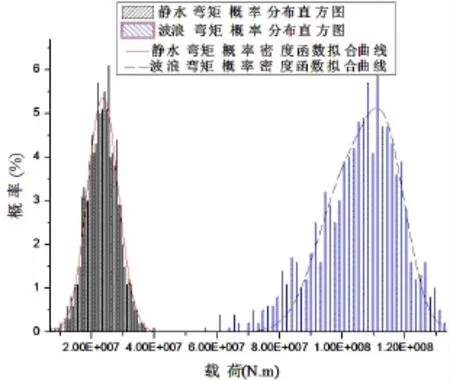
图4 船体载荷概率分布Fig.4 The probability distribution of ship hull loads

图5 船体载荷累积概率分布Fig.5 The accumulative probability distribution of ship hull loads

通过对图4、5所示的波浪载荷和静水弯矩的概率分布及累积概率分布的统计特征值进行分析，可得波浪载荷及舰艇静水弯矩的数字特征及其波动范围，如表3所示。

表3 静水弯矩及波浪载荷的数字特征Tab.3 The numerical characteristics of still bending and wavemoment

在确定了基本参数的数字特征后，在已建立的现役舰艇船体结构概率可靠性模型及非概率可靠性模型的基础上，分别对该舰艇的概率可靠性理论下的可靠性指标β、船体结构的可靠度Pr及非概率可靠性理论下的非概率可靠性指标η的时变性进行分析，计算结果如图6、7所示。

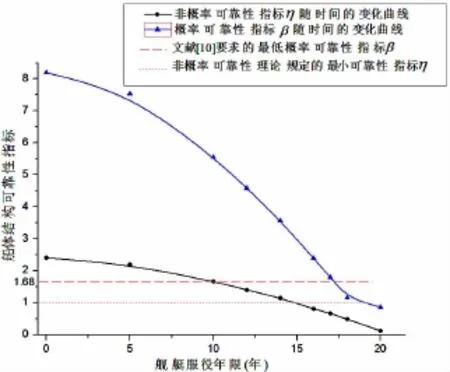
图6 现役舰艇结构可靠性指标时变曲线Fig.6 The time-varying curve of reliability index of warship structure in service

图7 现役舰艇结构可靠度时变曲线Fig.7 The time-varying curve of reliability of warship structure in service

由图6、7所示的船体结构可靠性及可靠度时变曲线可知：基于非概率可靠性评估方法，当该舰艇服役年限超过15年时η=0.817＜1.0，其船体结构开始处于不可靠状态；基于随机概率论的可靠性评估方法，当舰艇服役年限超过18年时β=1.16＜1.68，船体结构开始处于不可靠状态。按系统设计要求，结构的失效概率Pf（ Pf=1-Pr）不大于≤10-5，当舰艇服役期限超过17年时，船体结构失效概率Pf为10-3大于10-5，认为该舰艇结构已处于不可靠状态。通过上述的可靠性计算结果可知，基于非概率可靠性理论开展现役舰艇船体结构可靠性评估，其计算结果相对于概率可靠性理论的计算结果更偏于保守。在工程应用方面具有更好的适用性和实用性。

4 结 论

本文基于非概率可靠性理论和概率统计理论，结合描述抽样的蒙特卡洛数值模拟法（MCS），建立了现役舰艇随机概率可靠性及非概率可靠性分析模型，并通过实例计算与分析。主要结论归纳如下：

（1）采用概率统计理论开展现役舰艇船体结构可靠性评估虽然计算结果较为精确，但其对随机变量的数字特征非常敏感，在随机变量特征函数不确定的情况下其计算量相对较大，效率相对低；基于非概率可靠性理论的现役舰艇船体结构可靠性计算方法计算量小、计算效率高，不受随机变量分布类型、数字特征的影响，具有良好的适用性。

（2）基于非概率可靠性理论与概率统计理论对现役舰艇船体结构可靠性进行分析，两者计算结果相差不大，所以采用非概率可靠性分析方法计算现役舰艇结构的可靠性是可行的；由于非概率可靠性理论的计算结果偏于保守，所以该方法在工程应用中具有很强的实用性。

（3）相对于理论成熟的随机概率理论，目前非概率可靠性理论还尚未完善。引入非概率可靠性理论仅仅是对基于随机概率理论开展现役舰艇船体结构可靠性评估的有效补充。针对概率统计理论及非概率可靠性理论各自的特点，整合其各自优点开展舰艇船体结构的可靠性进行计算既能保证随机变量（如舰艇载荷的计算）的客观规律又能有效地减小计算量，提高计算效率。对于这种基于随机概率论和非概率可靠性理论混合模型在现役舰艇船体结构可靠性评估方面的应用有待进一步研究。

参 考 文 献：

[1]Mansour A E.Approximate probabilitymethod of calculating ship longitudinal strength[J].Journal of Ship Research,1974, 18(3):203-213.

[2]Paik JK.Ultimate longitudinal strength-based safety and reliability assessment of ship’s hull girder[J].Journal of the Society of Naval Architects of Japan,1991,169:403-414.

[3]冯国庆,邓进宁,任慧龙,等.船体结构屈服强度可靠性分析[J].华中科技大学学报（自然科学版）,2014,42(6):58-62. Feng Guoqing,Deng Jinning,Ren Huilong,et al.Reliability analysis of yielding strength of ship structures[J].Journal of Huazhong University of Science&Technology(natural science edition),2014,42(6):58-62.

[4]秦圣平,崔伟成,沈 凯.船舶结构时变可靠性分析的一种非线性腐蚀模型[J].船舶力学,2003,7(1):94-103. Qin Shengping,CuiWeicheng,Shen Kai.A non-linear corrosionmodel for time variant reliability analysis of ship structures[J].Journal of Ship Mechanics,2003,7(1):94-103.

[5]Lloyd’s Register.Naval Classification[K].2000.

[6]Fukuda J.Long-term predictions ofwave bendingmoment.Part Iand Part II[J].Journal of the Society of Naval Architects of Japan 1966,120;1968,123.

[7]Hoffman D,Lewis E.Analysis and interpretation of full scale data on mid ship bending stress of dry cargo ships[R].Ship Structure Committee,Report SSC_196,June 1969.

[8]中国船级社.钢制海船入级规范[S].北京:中国船级社,2012.

[9]杨代盛,桑国光,李维扬,等.船舶强度的概率方法[M].哈尔滨:哈尔滨工程大学出版社,2007.

[10]GJB/Z119-99.水面舰艇结构设计计算方法[S].

[11]孙海虹,肖桃云,张圣坤.考虑腐蚀影响的船体梁极限承载能力时变可靠性分析[J].中国造船,2000,41(2):49-57. Sun Haihong,Xiao Taoyun,Zhang Shengkun.Time-variation reliability analysis based on ultimate strength of corroding ship girders[J].Journal of Shipbuilding China,2000,41(2):49-57.

[12]Ben-Haim Y.A non-probabilistic conceptof reliability[J].Structural Safety,1994,14(4):227-245.

[13]郭书祥,吕震宙,冯元生.基于区间分析的结构非概率可靠性分析模型[J].计算力学学报,2001,18(1):56-62. Guo Shuxiang,LüZhenzhou,Feng Yuansheng.A non-probabilisticmodel of structural reliability based on interval analysis[J].Chinese Journal of ComputationalMechanics,2001,18(1):56-62.

Safety evaluation of non-probabilistic reliability model of vessels in service

HUA Lin,WU Fan,MU Jin-lei,LU Qing-liang
(Department of Naval Architecture Engineering,Naval University of Engineering,Wuhan 430033,China)

The non-probabilistic and stochastic probability reliability analysismodel under corrosion damage of the vessel in active service is established based on the non probabilistic reliability theory and probability statistics theory,and the Monte Carlo Simulation(MCS)of descriptive sampling is introduced to calculate the reliability of vessels in service.Simultaneously,the reliability of a large vessel is calculated by the two kinds of reliability analysismodel on the reliability of hull structure after corrosion,and the reliability of the two calculation results is compared and analyzed.The result shows that the non-probabilistic reliability both can highlight the objectivity of uncertain variables and low amount of calculation;high efficiency,conservative results,and has a very strong practicability in engineering application.

vessels in service;non-probabilistic reliability;probability statistics theory;Monte Carlo Simulation

U661.42 TB114.3

：Adoi:10.3969/j.issn.1007-7294.2017.02.008

2016-10-13

国家自然科学基金资助项目（5B09231）；国防基金项目资助（4355162345）

滑 林（1986-），男，海军工程大学博士研究生；

吴 梵（1962-），男，海军工程大学教授，博士生导师，E-mail:wufang.135@163.com。

1007-7294（2017）02-0184-08