船舶推进轴系纵横耦合非线性动力学分析—叶频激励下横向主共振响应
邹冬林,张建波,塔 娜,饶柱石
(上海交通大学 a.振动、冲击、噪声研究所;b.机械系统与振动国家重点实验室,上海 200240)
船舶推进轴系纵横耦合非线性动力学分析—叶频激励下横向主共振响应
邹冬林a,b,张建波a,b,塔 娜a,b,饶柱石a,b
(上海交通大学 a.振动、冲击、噪声研究所;b.机械系统与振动国家重点实验室,上海 200240)
在考虑Von Karman非线性位移—应变关系下,基于Hamilton变分原理建立了船舶推进轴系纵横耦合非线性动力学方程。利用Galerkin方法,导出系统第一阶模态振动微分方程,采用多尺度法求解该方程。获得了叶频激励下横向主共振响应方程组,利用伪弧长延拓法数值求解了该方程组的平衡解并分析了其稳定性。探讨了支承刚度、激励载荷、螺旋桨质量、阻尼比以及细长比对轴系纵横耦合效应的影响。研究表明:细长比越小,激励载荷越大,阻尼比越小,系统纵横耦合效应越强;增加后艉轴承刚度可以抑制纵横耦合效应,增加前艉轴承以及推力轴承刚度则增强纵横耦合效应,而中间轴承对其没有明显影响;与线性模型相比,纵横耦合效应使轴系横向共振时的频率大于其线性固有频率,在某些激励频率处,幅频响应曲线上存在多解使幅值出现跳跃现象。分析结果对船舶推进轴系的设计有指导意义。
船舶轴系;纵横耦合;多尺度法;主共振
0 引 言
船舶推进轴系作为船舶水中航行的动力系统,是船舶组件中非常重要的部件,因此对推进轴系的动力学特性分析一直以来都是国内外研究的热点[1-3]。早期对推进轴系的研究集中在线性振动问题的分析上,包含了固有频率、模态分析以及不平衡响应等等。当轴系跨度小、激励力较小而产生的振动幅值较小时,纵向与横向振动耦合作用较弱,两者分别为线性振动,可以采用线性振动理论进行分析计算。如文献[4]分析了不同中间轴承布置方案对船舶轴系力学性能的影响。文献[5]分析了不同位置不同支承长度的轴承条件下固有振动特性。文献[6]分析了艉轴承单点和双点支承下轴系的振动特性。然而简单的线性近似不能精确地给出系统动力学行为,也无法解释工程实际中的一些非线性现象。例如,多频现象,组合共振,参激振动,自激振动,极限环,分岔,振幅跳跃甚至混沌运动等非线性振动特有的现象。这些现象给工程设计带来隐患。仅研究线性振动问题无能为力,因此有必要建立系统的非线性动力学模型来加以分析。对于船舶轴系,一方面由于其跨度大,细长比小,当激励力较大时,容易引起轴系较大振动;另一方面其叶频有可能落在轴系第一阶横向固有频率内而引起共振,此时横向振动变得很大,进而其纵、横向变形之间的弹性耦合作用变得相当严重,从而引起轴系异常振动,所以研究轴系纵横耦合非线性振动有重要的意义。近年来国内外学者对纵横耦合引起的非线性现象给予了极大的关注。文献[7-8]利用有限差分法研究了海洋平台的立柱在纵横耦合下的自由振动与强迫响应。文献[9-10]利用伪弧长延拓法与数值积分法研究了轴向运动梁在纵横耦合作用下产生内共振时的能量渗透问题。文献[11]利用有限元法研究了简支梁在纵横耦合作用下的强迫振动。文献[12]利用增量谐波平衡法研究了轴向运动梁在纵横耦合作用下的内共振问题。文献[13]研究了变质量梁(火箭发射)在纵横耦合作用下的系统动力学行为。文献[14-16]利用多尺度法研究了转子在纵横耦合作用下的自由振动与主共振响应。文献[17]应用多尺度法研究了匀转速、顺臂安装下悬臂梁的主参激共振与外激励1/2次亚谐共振同时作用时梁的动力学响应。这些文献都充分揭示了梁或转子在纵耦合作用下的丰富的非线性动力学特性。
目前大多数模型都是针对简支梁或者悬臂梁模型,边界条件比较简单,难以满足工程实际需要。同时由于简支梁和悬臂梁的一阶纵向振动频率远离一阶横向振动频率,因而多数研究都是直接忽略纵向惯性的影响。然而船舶推进轴系是一个典型的多支承多质量系统,同时由于端部螺旋桨以及纵向推力轴承的影响,其纵向惯性很大,纵向振动对系统振动的影响将不可忽略。基于上述原因,本文针对船舶实际结构,考虑多支承及端部集中质量的影响,建立轴系纵横耦合动力学模型,考虑纵向惯性效应,研究当叶频接近第一阶横向固有频率轴系发生主共振时的动力学特性。分析结果对船舶推进轴系的设计具有一定的指导借鉴意义。
1 动力学模型
典型的船舶推进轴系由螺旋桨、后艉轴承、前艉轴承、中间轴承以及推力轴承组成,如图 1所示。为了简化分析,假设轴系具有均匀截面,螺旋桨简化为集中质量,各轴承简化为具有刚度的弹簧。
采用瑞利梁力学模型,考虑转动惯量忽略剪切变形的影响,利用Hamilton变分原理建立相应的非线性动力学方程。考虑Von Karman位移-应变关系[7],同时设O(u)~O( v2)~O(w2),即轴系纵向应变与横向应变相比为高阶小量。

图1 船舶推进轴系简图Fig.1 Schematic ofmarine propulsion shafting
轴系的势能由轴段应变能和支承弹簧的弹性势能组成,其表达式为:

式中前两项为线性应变能,后两项为弯纵耦合引起的非线性应变能。其中:E为弹性模量;A为轴段截面积;Id为截面惯性矩;L为轴系长度;u,v,w为分别为轴的纵向(x向),横向(y向)与垂向(z向)振动位移。

式中:kj为各径向轴承刚度;xj为螺旋桨到各径向支承的距离;kt为推力轴承刚度。类似地,轴系动能也由轴段动能与螺旋桨动能两部分组成:
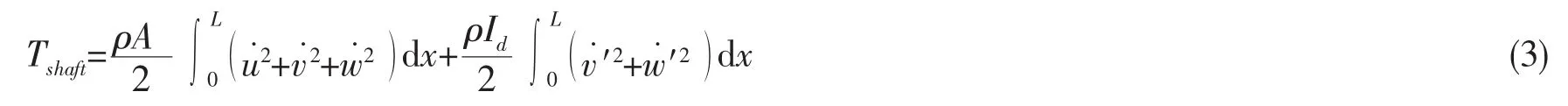
上式中没有包括旋转动能,因为旋转动能属于刚体转动,不产生变形。同时也忽略了陀螺效应的影响。

式中:M1为螺旋桨质量;Jd1为螺旋桨直径转动惯量。
外载荷做功包括随转频激励的不平衡载荷、随叶频激励的流体载荷以及纵向脉动载荷。由于本文只研究叶频激励下的轴系横向(垂向)主共振,为了简化分析,设其它载荷为零,只考虑叶频载荷。因此外载荷做功为:

式中:F为叶频激励载荷;α为相位;Ω为转速,假设为7叶桨。由Hamilton变分原理可得:代入动能、势能与外载荷功,引入狄拉克函数δ()x描述支承刚度的影响,可推得轴系弯纵耦合下

的振动偏微分方程为:

对应的线性边界条件为:
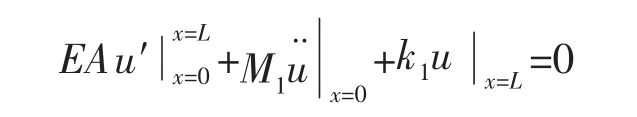
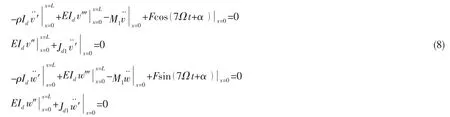
式中理论上应该是非线性边界条件,取为线性边界条件时一方面简化了分析,另一方面对系统全局动力学不会带来影响[18]。
2 方程无量刚化与离散
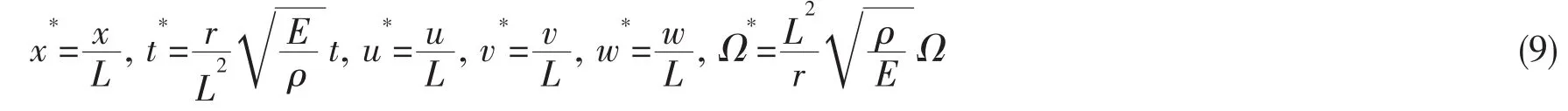
将(9)式代入(7)式中,去掉星号得:
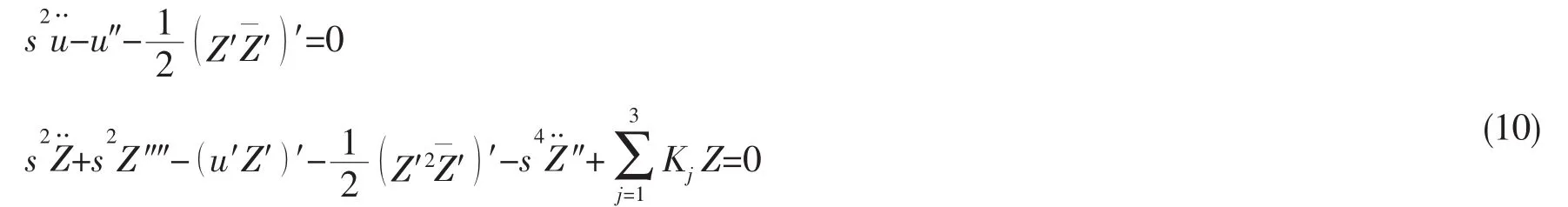
同理,(8)式也可以变为:
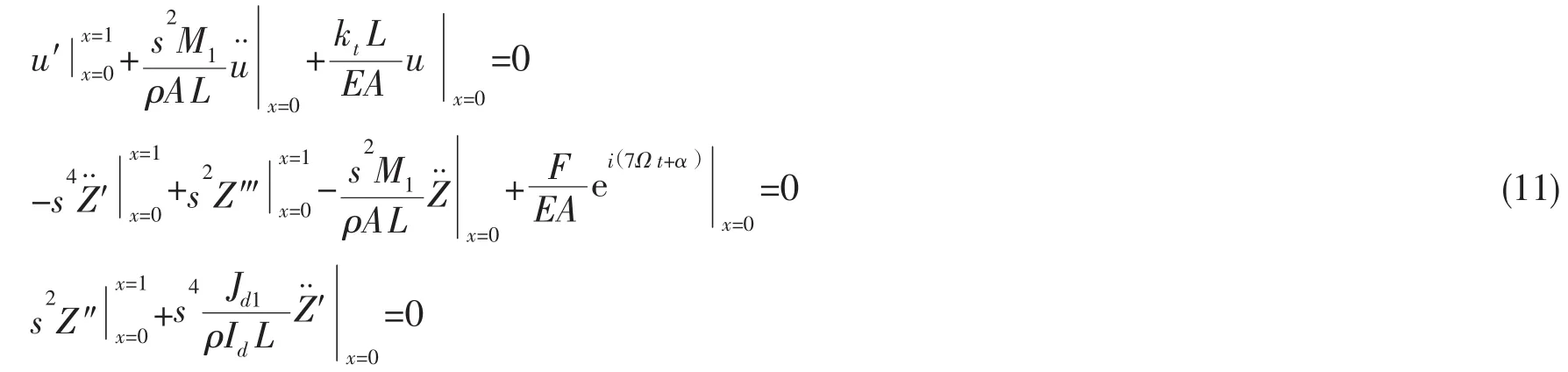
利用Galerkin方法将偏微分方程离散为常微分方程,试探函数采用线性模态振型。选取一阶模态,记
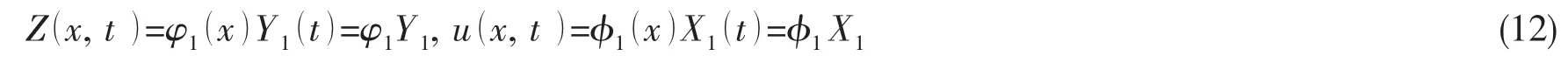
式中:φ1(x)为纵向第1阶模态振型;φ1(x)为垂向与横向第1阶模态振型。将(12)式代入(10)式得:

将(13)式乘以φ1(x),并积分得:
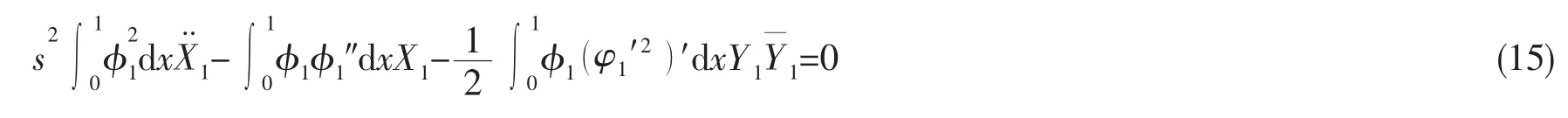
将(15)式分部积分并结合边界条件(11)式可得:
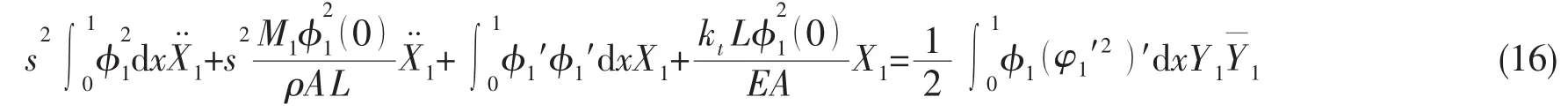
同理,(14)式也可化为:
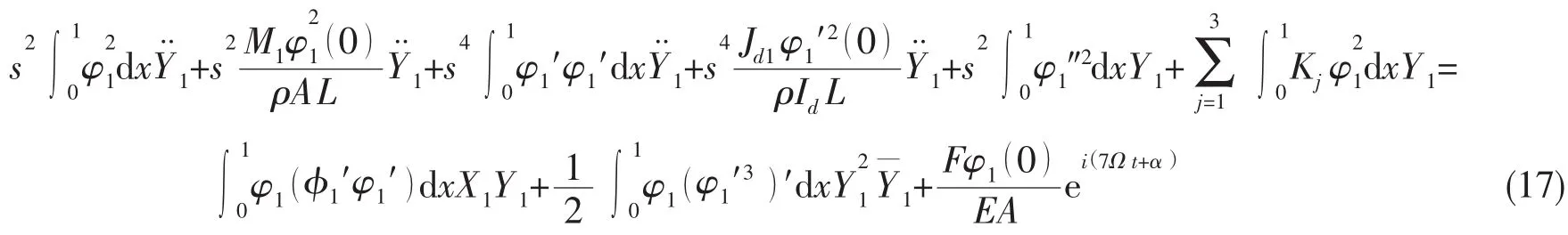
由于模态向量关于质量与刚度正交[19],假设模态振型按质量归一化,则有:
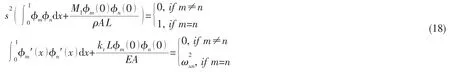
式中:ωun为纵向第n阶无量纲固有频率。
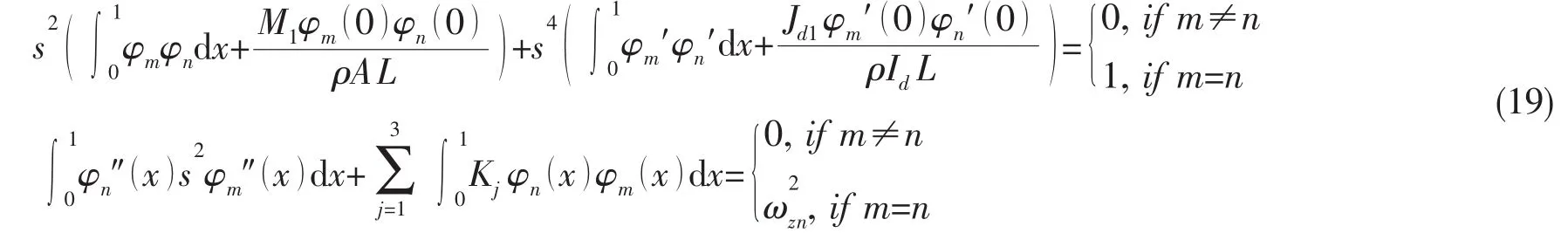
式中:ωzn为横向第n阶无量纲固有频率。
利用(18)式、(19)式,(16)式和(17)式分别可化为:
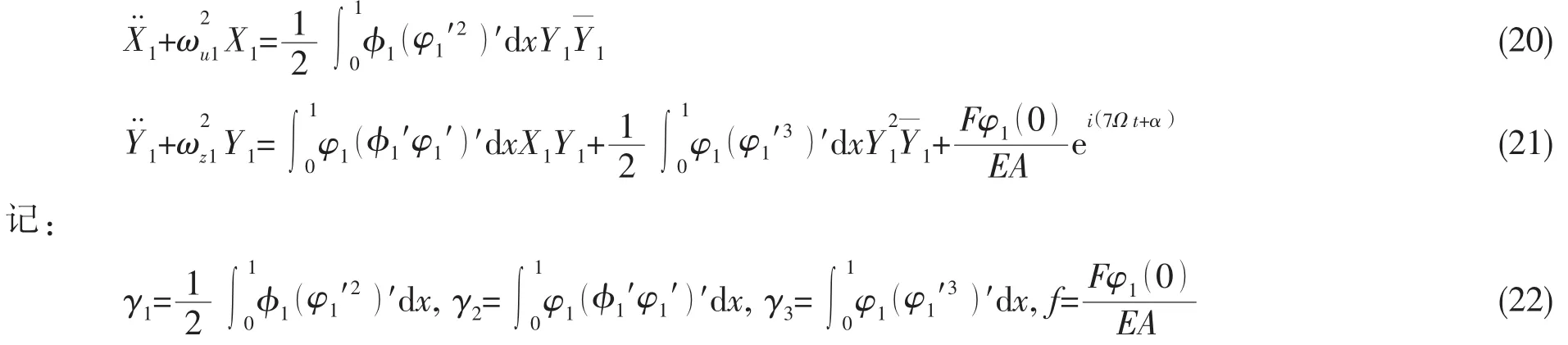
引入阻尼比,则(20)式与(21)式进一步可化为:

3 多尺度法求解方程
本文采用多尺度法来求解(23)式这一弱非线性问题。与正则摄动法相比,多尺度法的明显优点是不仅能计算周期运动,而且能计算耗散系统的衰减振动;不仅能计算稳态响应,而且能计算非稳态过程;可以分析稳态响应的稳定性,描绘非自治系统的全局运动性态[20]。本文只考虑一次近似解。引入小参数ε和两个时间尺度Tn=εn(t)(n=0,2),由求导法则得:

式中:Dn为偏微分算子符号,定义为
由于在推导轴系纵横耦合动力学方程时,假设O(u)~O( v2)~O(w2),所以设解的形式为:
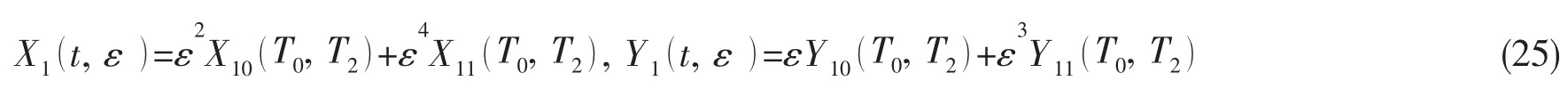
为了获得一致有效的近似解,必须使横向阻尼、激励载荷与非线性项均出现在同一阶方程上,为此设ξz1=ε2,f=ε2f*,代入(23)式并去掉星号后得各阶近似方程:
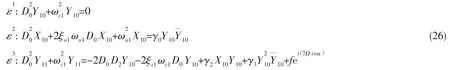
将一次近似方程的通解写成:

式中:A为待定复函数,由消去长期项得到。代入二次近似方程右边得:

其特解为:

代入三次近似方程得:

设7Ω-ε2σ=ωz1,其中σ为频率失调参数。代入(30)式消去长期项得:

把复数A写成极坐标形式:

代入上式,并分离实部与虚部:

令r=-θ+σT2+α,将上式化为自治系统得:
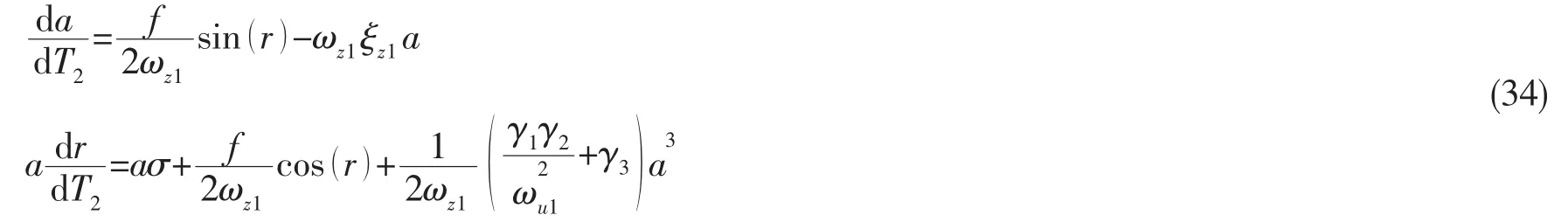


结合(12)式、(25)式、(27)式和(32)式,横向振动的一阶近似解为:

式中:a,r由(36)式决定。
对稳态解进行稳定性分析,对(34)式右端关于a,r求Jacobian矩阵:
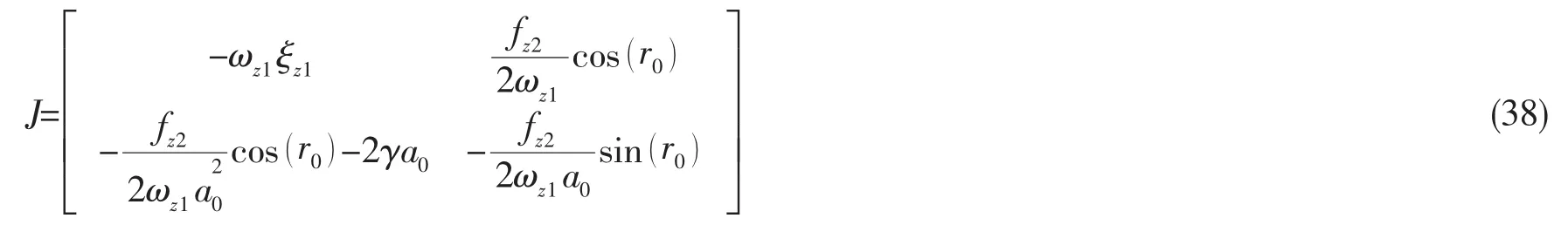
式中:a0,r0为满足(35)式的平衡解。(38)式的特征多项式为:

由稳定性理论可知,当(39)式的根全为负数时,平衡解稳定。由此可得稳定性条件为:

4 算例分析
以某一船舶推进轴系为算例,轴系长度14.5 m,外径240 mm,内径120 mm,轴系细长比s为 0.004 6,材料弹性模量210 GPa,密度7 800 kg/m3。轴系各支承参数:后艉轴承径向刚度2.5×108N/m;前艉轴承径向刚度0.8×108N/m;中间轴承径向刚度3×108N/m;推力轴承刚度3×108N/m。螺旋桨质量为6 t,直径转动惯量为3 000 kg·m2。假设横向叶频载荷F为1 000 N,阻尼比ξz1为0.01。表1是采用有限单元法求得轴系弯曲方向前两阶与纵向第一阶线性固有频率(不考虑轴向静推力)。

表1 轴系固有频率Tab.1 The frequency of the shaft
本文探讨各支承刚度、螺旋桨质量以及细长比对非线性参数γ的影响,揭示轴系纵横耦合效应的影响因素与规律。由(22)式可知,求取γ时要对各阶振型进行求导和积分运算。对于船舶推进轴系,由于边界条件复杂,难以求得振型的解析解,只能获取数值解。本文利用有限单元法求得振型的数值解,再将这些离散点拟合成B样条曲线,进而对B样条曲线进行求导与积分运算[21]。大量实例表明B样条曲线在数据较为稀疏的情形下拟合效果也很理想。
图2反应了轴系各参数对非线性参数 的影响。从图中可以得出:在一定范围内增大后艉轴承刚度可以抑制纵横耦合效应;在一定范围内增大前艉轴承刚度和推力轴承刚度可以增加纵横耦合效应;中间轴承对纵横耦合效应影响不明显;增大螺旋桨质量,减少细长比可以增加纵横耦合效应。
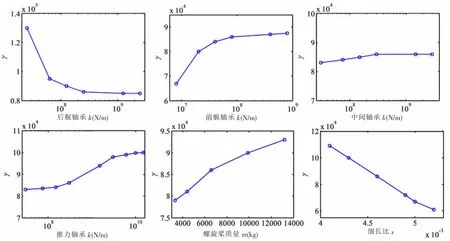
图2 轴系各参数对纵横耦合效应的影响Fig.2 Effectof the shaft parameters on the geometric nonlinear
采用伪弧长延拓法[22]数值求解(36)式,以σ为分岔参数,得到幅值频率响应曲线(计算参数由前面给出)。图3是考虑与不考虑纵横耦合作用下幅频响应曲线对比(本文所计算的响应均为靠螺旋桨处)。左边的图是不考虑纵横耦合时的幅频曲线,右边是考虑其影响时的幅频曲线。由此可得,纵横耦合效应使轴系共振时的频率略大于其线性固有频率,从而使幅频曲线向右弯曲。对于某些σ值,系统存在三个解,其中有两个解是稳定的,一个解是不稳定的(CD间的解不稳定),使得幅频曲线上出现了振幅跳跃现象。在升速时,轴系振幅沿A→B→C跳跃到E→F路径变化;降速时沿F→E→D跳跃到B→A路径变化;在BE以内,轴系振幅在BC与DE间来回变化。这种跳跃性会使轴系产生应力突变,引起疲劳断裂,工程中应避免。
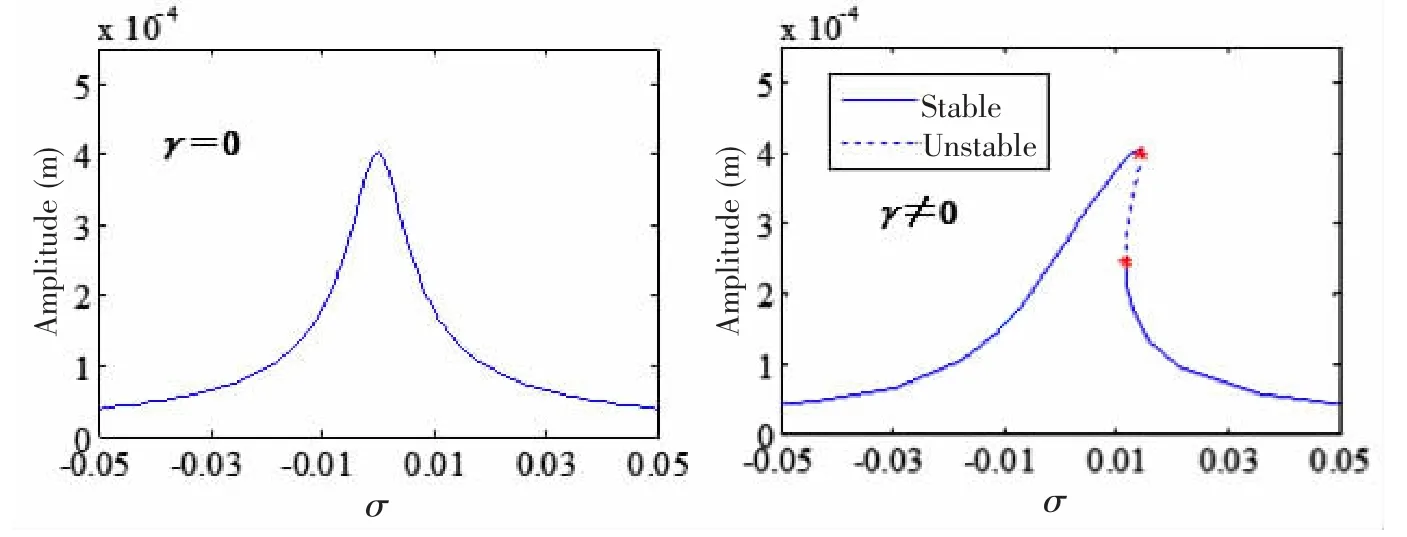
图3 线性与非线性下幅频响应曲线对比Fig.3 Comparison of linear and nonlinear response curves
图4反应不同载荷下的幅频响应曲线对比,其中计算参数在上面已给出;图 5反应不同阻尼比,不同载荷下的幅频响应曲线对比,计算时细长比取为0.004 6;图 6反应轴系不同细长比,不同载荷时幅频响应曲线对比,计算时阻尼比取为0.01。从各图中可以得出,随着载荷的增加,纵横耦合效应越强;阻尼比越小时,纵横耦合效应越强;细长比越小时,纵横耦合效应越强。

图4 不同载荷下幅频响应曲线对比Fig.4 Response curve comparison of different excitation loads
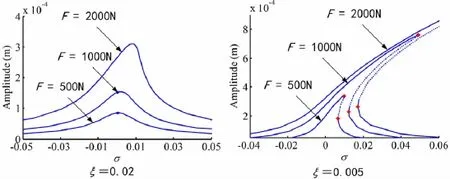
图5 不同阻尼比下幅频响应曲线对比Fig.5 Response curve comparison of different damping ratios

图6 不同细长比下幅频响应曲线对比Fig.6 Response curve comparison of different slender ratios
5 结 论
本文应用Hamilton变分原理建立了轴系纵横耦合非线性动力学方程。利用多尺度法研究了横向振动在叶频激励下的主共振动力学特性,研究表明:(1)与线性模型相比,由于纵横耦合效应使轴系横向产生共振时的频率略大于其线性固有频率,同时在幅频响应曲线上存在多解使幅值出现跳跃现象;(2)在一定范围内增大后艉轴承刚度可以抑制纵横耦合效应,增大前艉轴承刚度与推力轴承刚度可以增加纵横耦合效应,而中间轴承对纵横耦合效应影响不明显;(3)增大螺旋桨质量,减少细长比可以增加纵横耦合性效应;激励载荷越大,阻尼比越小时,系统纵横耦合效应越强。
[1]邹冬林,刘 翎,饶柱石,塔 娜.利用有限元法与打靶法的纵横耦合轴系主共振分析[J].振动工程学报,2016(29): 87-95. Zou Donglin,Liu Ling,Rao Zhushi,Ta Na,Primary resonance of shaftswith coupled longitudinal transverse vibration by finite elementand shootingmethods[J].Journal of Vibration Engineering,2016(29):87-95.
[2]邹冬林,荀振宇,饶柱石,塔 娜.主共振与内共振下纵横耦合轴系动力学分析[J].振动工程学报,2016(29):511-520. Zou Donglin,Xun Zhenyu,Rao Zhushi,Ta Na,Dynamics of the coupled longitudinal-transverse shafts under primary and internal resonances[J].Journal of Vibration Engineering,2016(29):511-520.
[3]Zou D L,Liu L,Rao Z S,Ta N.Coupled longitudinal-transverse dynamics of amarine propulsion shafting under primary and internal resonances[J].Journal of Sound and Vibration,2016(372):299-316.
[4]王宏志,魏海军,关德林,等.中间轴承对船舶轴系力学状态影响的数字模拟[J].船舶力学,2006,10(1):98-105.Wang Hongzhi,Wei Haijun,Guan Delin,et al.Numerical simulation on ship shaftingmechanics condition of intermediate bearing[J].Journal of Ship Mechanics,2006,10(1):98-105.
[5]周春良,刘占生,郑洪涛.轴承支承长度及间距对船舶轴系振动特性影响[J].船舶工程,2007(05):16-18. Zhou Chunliang,Liu Zhansheng,Zheng Hongtao.Bearing stiffness to ship shafting system vibration performance[J].Ship Engineering,2007(05):16-18.
[6]Murawski.Shaft line whirling vibrations:Effects of numerical assumptions on analysis results[J].Marine Technology,2005, 42(2):53-60.
[7]Han SM,Benaroya H.Non-linear coupled transverse and axial vibration of a compliant structure,Part 1:Formulation and free vibration[J].Journal of Sound and Vibration,2000,237(5):837-873.
[8]Han SM,Benaroya H.Non-linear coupled transverse and axial vibration of a compliant structure,Part 2:Forced vibration [J].Journal of Sound and Vibration,2000,237(5):875-900.
[9]Ghayesh M H,Kazemirad S,AmabiliM.Coupled longitudinal-transverse dynamics of an axiallymoving beam with an internal resonance[J].Mechanism and Machine Theory,2012,52(12):18-34.
[10]Ghayesh M H,Farokhi H,AmabiliM.In-plane and out-of-planemotion characteristics ofmicrobeamswithmodal interactions[J].Composites Part B:Engineering,2014,60(1):423-439.
[11]胡 义,杨建国.梁纵横耦合振动研究[J].武汉理工大学学报(交通科学与工程版),2010(03):537-541. Hu Yi,Yang Jianguo.Studies on the longitudinal and lateral coupled vibration of beam[J].Journal ofWuhan University of Technology,2010(03):537-541.
[12]黄建亮,陈树辉.纵向与横向振动耦合作用下轴向运动梁的非线性振动研究[J].振动与冲击,2011(08):24-27. Huang Jianliang,Chen Shuhui.Study on nonlinear vibration of an axiallymoving beam with coupled transverse and longitudinalmotions[J].Journal of Vibration and Shock,2011(08):24-27.
[13]梁 昆,邢誉峰.变质量梁纵横耦合振动特性研究[C]//北京力学会第20届学术年会.中国北京,2014.
[14]Hosseini SA A.Dynamic stability and bifurcation of a nonlinear in-extensional rotating shaftwith internal damping[J]. Nonlinear Dynamics,2013,74(1-2):345-358.
[15]Hosseini SA A,Zamanian M.Analytical solution for general nonlinear continuous systems in a complex form[J].Applied Mathematical Modelling,2013,37(3):1163-1169.
[16]Hosseini SA A,et al.Vibration analysis of geometrically nonlinear spinning beams[J].Mechanism and Machine Theory, 2014,78(0):15-35.
[17]吴 涛,冯志华,胡海岩.定轴转动与基础激励下梁的非线性动力学[J].振动工程学报,2003(01):15-20. Wu Tao,Feng Zhihua,Hu Haiyan.Nonlinear dynamics of flexible beam under rotation and axially parametric joint excitation[J].Journal of Vibration Engineering,2003(01):15-20.
[18]Pesheck E,Pierre C,Shaw SW.Modal reduction of a nonlinear rotating beam through nonlinear normalmodes[J].Journal of Vibration and Acoustics,2002,124(2):229-236.
[19]克拉夫R,彭津 J.结构动力学[M].北京:高等教育出版社,2006. Clough R,Penzien J.Dynamics of Strcutures[M].Beijing:Higher Education Press,2006.
[20]刘延柱,陈立群.非线性振动[M].北京:高等教育出版社,2001. Liu Yanzhu,Chen Liqun.Nonlinear vibration[M].Beijing:Higher Education Press,2001.
[21]薛定宇,陈阳泉.高等应用数学问题的MATLAB求解[M].北京:清华大学出版社,2008. Xue Dingyu,Chen Yangquan.Advanced applied mathematical problem solutions with MATLAB[M].Beijing:Tsinghua University Press,2008.
[22]Nayfeh A H,Balachandran B.Applied nonlinear dynamics:Analytical,computational,and experimentalmethods[M]. JohnWiley&Sons,Inc.1995.
Coupled longitudinal-transverse nonlinear dynam ics of amarine propulsion shafting—Primary resonance under blade frequency excitation
ZOU Dong-lina,b,ZHANG Jian-boa,b,TA Naa,b,RAO Zhu-shia,b
(a.Insitute of Vibration,Shock and Noise;b.State Key Laboratory ofMechanical System and Vibration, Shanghai Jiao Tong University,Shanghai200240,China)
Based on Hamilton’s principle and considered the Von Karman’s nonlinear strain-displacement relationship,a coupled longitudinal-transverse nonlinear dynamic model of amarine propulsion shafting is established.The firstmode equations are obtained by Galerkin method and are solved by themethod of multiple scales.The primary resonance equations are derived under the blade frequency excitation.Then, these equations are numerically solved by pseudo-arclength continuationmethod to obtain the steady-state response and the stabilities are analyzed.The influence to the nonlinear effect is discussed about the support stiffness,load,mass of propeller,damping ration and slender ration.Research shows the smaller the slender ration,the bigger the load and the smaller the damping ration is,then the bigger the nonlinear effect is. The nonlinear effect is reduced by increasing the back stern bearing stiffness and increased by increasing the front stern bearing and thrust bearing stiffness.While themiddle bearingmakes no influence to it.Compared with the linearmodel,the lateral resonant frequency is bigger than the linear natural frequency.Insome frequencies,there are multiple solutions in amplitude-frequency curve and has jump phenomena. These analyses have a reference and guidance to the design ofmarine propulsion shafting.
marine shafting;coupled longitudinal-transverse;multiple scales;primary resonance
O322 TH113.1
:Adoi:10.3969/j.issn.1007-7294.2017.02.010
2016-07-21
邹冬林(1987-),男,博士研究生,E-mail:zoudonglin.520@sjtu.edu.cn;
饶柱石(1962-),男,教授,博士生导师,E-mail:zsrao@sjtu.edu.cn。
1007-7294(2017)02-0201-10

