声激励简单导管的声辐射特性研究

郑 晗，王 玮，周其斗

（1.海军装备研究院，北京100161；2.海军工程大学 舰船工程系，武汉430033）

声激励简单导管的声辐射特性研究

郑 晗1，王 玮1，周其斗2

（1.海军装备研究院，北京100161；2.海军工程大学 舰船工程系，武汉430033）

采用NASTRAN无限元技术，对简单导管受声激励的声辐射特性进行了研究，建立了导管声波模态和辐射声能量之间的直接联系，并考虑了导管半径、长度、长径比三种因素对管内声波模态、管外辐射声功率和远场声指向性的影响。研究结果表明：影响导管声波模态和辐射声功率的参数主要有两个，一是无因次波数，二是导管长径比；导管的长径比越小，总辐射声能量变小，但侧方屏蔽效应也变差，因此需综合考虑长径比变化对总辐射声能量和声指向性的影响；和导管的侧方屏蔽效应主要作用于中高频，低频时导管外的声场与入射声场基本相同。

导管声学；声源激励；单极子

0 引 言

导管受声激励下的声辐射特性分析，对于优化航空发动机、泵喷推进器和导管螺旋桨等导管结构[1]的声学设计，具有十分重要的意义。以往的研究中，对于导管声学计算方法的关注较多[2-6]，对管内外声场和声辐射特性的关注却比较少。

Doak[7-8]推导了声源分布于有限长导管内的声场声压和声功率公式，指出对于刚性有凸缘导管，决定声场的主要是三个因素：导管横截面几何、管内声源分布的时域和空间域特性和导管端口的边界条件。Wang和Tszeng[9]针对有限长导管，推导了一种新的计算开口广义辐射阻抗的公式，并指出，导管端口对整个声场的影响在高频、旋转声源及长导管情况下更加突出。这些研究主要从数学和公式推导的角度分析了导管声场，对于管内外声场如何发生联系，以及导管尺寸因素如何影响声辐射特性，并没有给出具体的分析。

本文以简单刚性导管为研究对象，采用基于NASTRAN无限元技术的导管声学计算方法，详细阐述了管内声波模态与管外辐射声功率的关系，并研究了导管尺寸对其降噪效果和屏蔽特性的影响，给出了具体的结论和建议。

1 模型和方法说明

如图1（a）所示，一简单刚性导管长为L，半径为a，长径比σ=L/D=L/2a，流体介质为水，单极子声源置于导管正中心，源强度A=1 kg/s2，计算频段为0-4 000 Hz，有限元模型如图1（b）。文献[10]中已经详细说明了有限元建模的具体方法和计算参数设置，并验证了采用NASTRAN无限元技术计算导管声场的正确性，指出其优势在于适用于任意多连通域问题的声场预报，适应任意复杂的导管截面和形状，并能考虑导管壁的弹性振动。

本文将基于该方法，分析简单导管的声辐射特性，并讨论导管尺寸变化对管内外声场的影响规律。除特别说明，在研究半径的影响时，固定导管长度L=1m，导管半径分别取a=0.125m，0.25m，0.5 m，1m；研究长度的影响时，固定导管半径a=0.5m，导管长度分别取L=0.5m、1m、2m和4m。

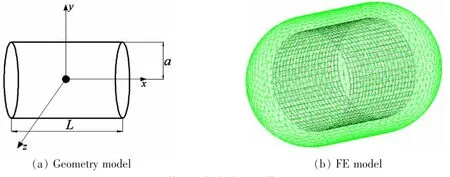
图1 导管的几何与有限元模型Fig.1 Geometry and FEMmodel of duct

2 导管内声场

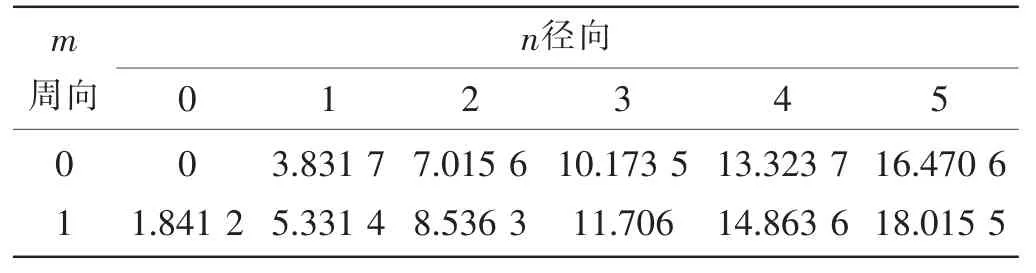
表1 Jmn′（xmn）=0的解Tab.1 Solutions of Jmn′（xmn）=0

首先对传统的无限长导管声波模态理论进行简要阐述，对一半径为a的无限长导管，管内声压的一个特解为[11]

其中：m和n分别为导管的周向和径向模态数；Amn为声压幅值；Jm（kmnr ）表示宗量为（kmnr ）的m阶柱贝塞尔函数，kmn=xmn/a，xmn是Jm′（xmn）=0的第n个零点（表1）；ω为声源角频率，kx为周向声波数，并且满足

当声波圆频率低于（m, n ）次简正波对应的简正频率，即k＜kmn时，kx为虚数，管内只能传播（m, n）阶以下的声波，此时也称（m, n ）阶声波模态被截止，k＞kmn时称为被打开。将临界条件k=kmn转化为ka=kmna=xmn，右边的xmn为常数，可见决定无限长导管声波模态打开或截止（即管内声场分布）的参数为ka。

公式（1）中，贝塞尔函数z=Jm（kmnr）=Jm（xmnr/a ）表示无限长导管内任一截面处的声压分布，取周向模态数m=0，借助表1中的xmn值，就可以得到无限长导管内第1-6阶径向声波模态的云图，如图2所示，该云图的形状与半径a无关。

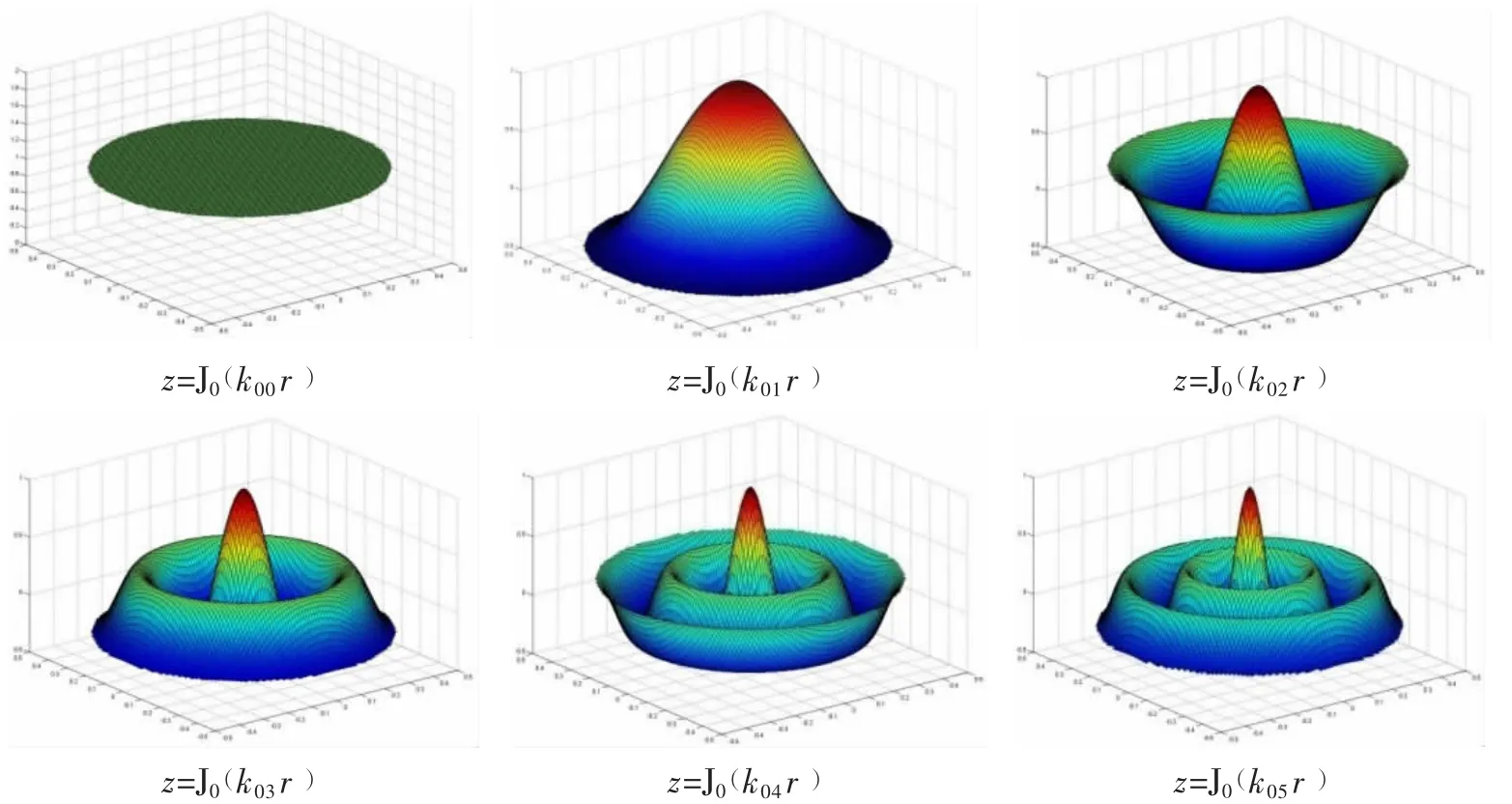
图2 无限长导管内的声场云图Fig.2 Sound field contour inside the infinite-length duct

2.1 半径的影响

下面研究有限长导管内的声场，对a=0.125 m，0.25m，0.5 m，1 m四种不同半径导管，计算单极子声源激励下的管内声场。假定导管长为单位1，中心截面为x=0，左右两端分别为x=-0.5和0.5，取x= 0.25截面处的导管内声场侧视图进行观察。图3给出了四种导管在取不同ka值时的管内声场截面云图，它们的周向模态数均为0。

比较图2和图3可以发现，具有相同ka值的不同半径导管的管内声场云图形状基本一致，并且与无限长导管内声场具有对应关系，ka=0.63对应J0（k00r）的平面波形式，ka=1.88对应J0（k01r）的径向（0,1）声波模态……ka=7.54对应J0（k04r）的径向（0,4）声波模态。这说明，有限长导管内的声场主要由参数ka决定，与导管半径a和声源频率f均有关系，有限长导管内的声波模态仍然遵循传统的无限长导管声波模态理论。

需要说明的是，由于导管端口边界的影响，在有限长导管中很难找到一个明显的分界频率点，以区分一个声波模态和另一个声波模态，这也正是有限长导管与无限长导管不同的地方，尽管管内声波模态的基本形式相同，但出现的频率位置却并不相同。

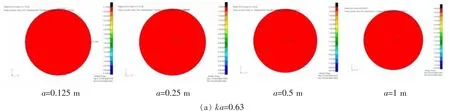
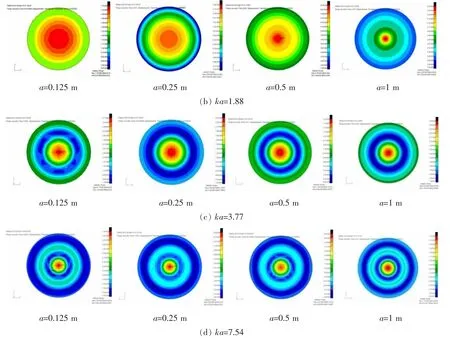
图3 不同半径的有限长导管内声场云图Fig.3 Sound field contour inside the finite-length ductwith different radius

2.2 长度的影响

如图4所示，给出了导管取四种不同长度L=0.5m、1m、2m和4m时的管内声场，四种导管的声场云图形状没有差别，这与Tyler和Sofrin在文献[2]中的论述一致。他们指出，导管长度对于管内声场并不十分重要，它只在一个很窄的频段内发挥作用，当激励频率远小于截止频率，即f＜＜fq时，衰减波数为

压力的衰减因子为p（x）=e-2πx/λq。这意味着，在长度等于截止频率对应波长λq=c/fq的导管里，压力将下降20log（e2π），大约50 dB。

图4 不同长度的导管内声场云图ka=4.62Fig.4 Sound field contour inside the finite-length ductwith different length ka=4.62

3 声源在导管中的辐射声功率

刚性导管受声源激励时不会产生振动，因此不会直接向外辐射声，本文中的“导管声辐射”指的是声源置于导管中时产生的辐射声。通常，在计算结构的辐射声功率时，要在一个封闭面上进行数值积分。然而，导管是一个具有开口的多连通域结构，不具有封闭结构面，因此，在导管外人为地建立一个封闭的声场球面，通过NASTRAN计算求出声场节点的速度和声压，再在声场球面上积分，就可以得到导管的辐射声功率和声功率级

式中：N为声场球面的单元数目，pi和vi为第i个声场单元上的平均声压和平均速度，“*”表示取共轭值，声功率的参考值为Wref=10-12（W）。将计算得到的声场结果文件（含有节点位移和速度）进行处理，采用FORTRAN语言编程，就可以得到导管的辐射声功率，程序的正确性作者已通过与自由声场中点声源辐射声功率的理论值进行了比较验证，这里不再赘述。

3.1 半径的影响

对a=0.125m、0.25m、0.5m和1m四种不同半径的导管，计算单极子声源激励下的导管辐射声功率值，声功率图以无因次波数ka为横坐标，如图5所示。同时给出的还有单极子声源入射声场的声功率曲线，其理论值[11]为，声功率级66.22 dB。观察声功率曲线，可以发现：

图5 不同半径导管的辐射声功率Fig.5 Radiated power of ductswith different radius

（1）从整体上看，以ka为横坐标的四条声功率曲线形状和趋势十分相似，均经历了三个主波峰和两个主波谷，且波峰和波谷的位置基本重合，好像可以用一条曲线（如a=1 m曲线）拟合出四种不同半径导管声功率随ka变化的趋势。这说明，ka是决定导管辐射声功率的一个非常重要的参数，因为ka决定了导管内声波模态的基本形式和第（m,n）阶模态出现的具体位置，所以也就决定了导管辐射声功率主波峰和波谷出现的位置。

（2）再看曲线的局部特征，以a=0.125 m曲线为例说明，对三个主峰和前两个主峰之间的4个次峰作垂线相交于横轴，找到对应的频率值，并提取相应的导管轴向声波模态，如图6所示。可以看到，导管辐射声功率的峰值与轴向声波模态数（记为p），即管内声场的轴向波峰数目有着直接关系。模态数为1时，辐射声功率出现主峰；模态数为3、5、7等奇数时，辐射声功率出现次峰，并且峰值随着模态数的增大而减小。这是因为，有限长导管内的声波要受到管口边界反射的影响，因此管内轴向声波模态会产生不同数目的波峰，当模态数为1时，管内声波受边界反射的影响最小，声波被反射回来的比例最小，辐射效率最高，因而辐射声功率的峰值最大；当模态数增大为3、5、7时，声波被反射回来的比例增大，辐射效率降低，因而辐射声功率峰值也依次减小。波谷位置对应的管内轴向声波模态数为2、4等偶数，如图7所示，此时管内正中位置的声压值最小，与声源发出的声波相互抵消，辐射效率最低，辐射声功率也最小，因此出现声功率曲线上的波谷。

图6 辐射声功率波峰对应的导管轴向声波模态Fig.6 Axial acoustic wavemodes of duct corresponding to the peak of the radiated power curve

图7 辐射声功率波谷对应的导管轴向模态Fig.7 Axial acoustic wavemodes of duct corresponding to the peak of the radiated power curve

绘图表示声功率曲线波峰、波谷与轴向模态数p的对应关系，如图8所示，随着声源频率的增大，导管轴向声波模态数p先从1开始增大到最大值，然后又逐渐减小到1，对应的声功率曲线从一个主峰值转到另一个主峰值，中间还经历了多个峰值和谷值。进一步的观察还可以发现，在相邻的两个主波峰之间，尽管管内声波的轴向模态数p不尽相同，但径向和周向模态数（m,n）却是相同的，这也再次印证了上一条结论。

（3）比较四条辐射声功率曲线的主峰值大小，可以看到，导管的半径越小，声功率的峰值就越大。这是因为，点声源的辐射声功率要受到环境的影响，根据文献[12]中的公式推导，当一个点声源十分靠近无限大刚性面时，点声源的辐射声功率是自由空间中辐射声功率的两倍，声功率级高约3 dB，即声功率的大小受环境的影响。由此可以解释这个现象：声源在半径小的细导管中受到端口边界条件的影响更大，声功率级相比入射声场的增加值更大。

（4）比较四条辐射声功率曲线的峰值数目，可以看到，导管的半径越小，声功率曲线的次波峰和波谷数目越多，曲线的振荡越厉害。这是因为半径小的细导管相比粗导管具有更为丰富的轴向声波模态，轴向模态数p的取值更多，由于每个p值都对应一个波峰或者波谷，因而峰值的数目更多。

3.2 长度的影响

图9给出了四种不同长度导管的辐射声功率曲线，它与图5中的曲线形状十分相似，L=0.5 m对应前面的a=1 m，L=1 m对应前面的a=0.5m……这些对应的曲线都具有同样的长径比，由此猜测，直接影响辐射声功率的导管参数不是半径，也不是长度，而是导管的长径比。下面将验证这个猜测。

3.3 长径比的影响

对前面两个系列计算中具有相同长径比的导管辐射声功率进行比较，如图10所示，可以看到：具有相同长径比的两导管辐射声功率曲线形状完全一致，由此验证长径比是真正影响辐射声功率的导管参数，3.1节中关于半径对导管声辐射影响的结论可全部转换为长径比的结论，对主要结论归纳总结如下：

（1）声源在刚性导管中的辐射声功率是一个随频率变化的量，其辐射声功率曲线与管内声场的内在联系表现为：无因次波数ka的大小决定了管内声场的形态，即管内声波模态数（m,n,p），其中径向和周向模态数（m,n）决定了辐射声功率出现主峰值的位置，即曲线的整体特征；而轴向模态数p决定了辐射声功率出现次波峰和次波谷的位置，即曲线的局部特征。（2）导管的长径比越大，其辐射声功率的主峰值越大，峰值的数目也越多。

图8 辐射声功率曲线的波峰波谷与模态数p的对应关系Fig.8 The relationship between the peak of radiated power curve and mode number p

图9 不同长度导管的辐射声功率Fig.9 Radiated power of ductswith different length

图10 不同长径比导管的辐射声功率Fig.10 Radiated power of ductswith different ratio of length to diameter

4 导管外声场指向性

导管的辐射声功率反映的是声源在导管中辐射声能量的总大小，而声指向性则反映了声源在导管中发声形成声场的方向性特征。设计一个声学性能优化的导管，不仅要抑制总能量的大小以降低噪声，还要关注一些特定方向的声压级，发挥屏蔽作用。本节将讨论管外声场的指向性，固定导管长度l= 1m，导管半径分别取为a=0.125m、0.25m、0.5m和1m，研究长径比σ变化对管外声场指向性的影响。

选取图5中第1～3个主波峰和第1～2个主波谷对应的无因次波数ka=0.2、4、7.3和ka=3.5、7，绘出不同长径比的导管在10m半径处的远场声指向性图，如图11所示。其中，无导管存在时的入射声场声压），声压级96.99 dB。

观察可以发现：（1）辐射声功率主波峰位置对应的声场指向性图（a）、（c）、（e）中，声压级大于入射声场声压级；而主波谷位置对应的声场指向性图（b）、（d）则恰好相反。由此可见，采用辐射声功率和远场声压级来判断导管的降噪效果在一定程度上是等效的。（2）声场指向性图（b）、（d）中的90°方向声压级小于自由声场声压级，这一现象被称之为“侧方屏蔽效应”[3]。显然，σ=4导管的侧方屏蔽效应最好，并且依次好于σ=2，1，0.5导管。这说明，导管的长径比越大，其侧方屏蔽效应也越好，因此可以通过增大长径比的方法抑制导管90°方向的噪声。（3）比较相同ka值下的不同长径比导管外声场指向性，长径比越大，管外声场指向性越复杂，波瓣数目也越多，这是因为细导管相比粗导管拥有更丰富的轴向声波模态。（4）当声源频率较低时，四种导管的声场指向性图十分接近，并且与点声源的入射声场一样没有指向性。这是因为声源的频率很小，其波长比导管半径大很多，导管的存在对声传播的影响很小，大部分入射声波可以绕过导管传播，发生声波的绕射（或衍射）现象，因此表现出很弱的指向性。随着频率的增加，导管端口边界的影响逐渐增强，辐射声场表现出较强的指向性，此时对噪声的预报和控制都将变得更加困难。

图11 不同波数激励下的声指向性图Fig.11 Directivity of sound with differentwave number at sound field radius 10m

5 结论与展望

（1）有限长导管内的声波模态仍然遵循传统的无限长导管声波模态理论，但由于端口辐射阻抗的影响，同一阶声波模态出现的频率位置不同。导管半径对管内声场的影响表现为，具有相同ka值的不同半径导管的管内声场云图形状基本一致，且与无限长导管内声场云图一一对应，导管长度对管内声场的影响较小，主要表现在远低于截止频率的频段。

（2）声源在刚性导管中的辐射声功率是一个随频率变化的量，其辐射声功率曲线与管内声场的内在联系表现为：无因次波数ka的大小决定了管内声场的形态，即管内声波模态数（m,n,p），其中径向和周向模态数（m,n）决定了辐射声功率曲线出现主峰值的位置，即曲线的整体特征；而轴向模态数p决定了辐射声功率曲线出现次波峰和次波谷的位置，即曲线的局部特征。

（3）导管的长径比越小，辐射声功率的主峰值越小，峰值数目也越少，对于抑制总辐射声能量的大小越有利；但是，长径比小的导管侧方屏蔽效应差，对于抑制导管90°方向的声压级却不利；因此，在导管的声学设计中，必须兼顾长径比变化对总辐射声能量和某方向声压级大小的影响，使导管总的降噪效果和特定方向上的屏蔽特性达到相对最优。

（4）导管内外声场形状的复杂程度与两个因素有关，一是声源频率，二是导管的长径比，频率和长径比的增大都将使管内声波模态数和管外声场的波瓣数增多。

（5）导管的侧方屏蔽效应主要作用于中高频，低频时导管外的声场与入射声场基本相同。

下一步，可利用简单导管声学特性的结论，研究复杂导管（如导管螺旋桨、泵喷推进器、分支型导管）的声学特性，并提出具体的降噪措施。

[1]刘忠族,孙玉东,吴有生.管道流固耦合振动及声传播的研究现状及展望[J].船舶力学,2001,5(2):82-90. Liu Zhongzu,Sun Yudong,Wu Yousheng.Current situation and trends on the study of coupled fluid-structure vibration and sound propagation of pipeline systems[J].Journal of Ship Mechanics,2001,5(2):82-90.

[2]Tyler JM,Sofrin TG.Axial flow compressor noise studies[J].SAE Transaction,1962,70:309-332.

[3]MyersM K.Radiation of sound from a point source in a short duct[C].NASA CP-3352,1997:19-26.

[4]杨迎春,周其斗,潘雨村.有限长导管声场预报的一种边界元方法[J].声学学报,2011,36(1):60-65. Yang Yingchun,Zhou Qidou,Pan Yucun.Boundary elementmethod for sound field prediction of finite duct[J].Acta A-custica,2011,36(1):60-65.

[5]杨迎春,周其斗,卢东庆.一种计算内外域声场的简单源方法[J].海军工程大学学报,2011,23(3):67-71. Yang Yingchun,Zhou Qidou,Lu Dongqing.Simple sourcemethod for sound field prediction in coupled interior/exterior domain[J].Journal of Naval University of Engineering,2011,23(3):67-71.

[6]柳贡民,李艳华.考虑流固耦合的多分支管道系统振动研究[J].船舶力学,2012,16(5):532-541. Liu Gongmin,Li Yanhua.Research on vibration ofmulti-branched pipe system considering fluid-structure interaction[J]. Journal of Ship Mechanics,2012,16(5):532-541.

[7]Doak P E.Excitation,transmission and radiation of sound from source distributions in hard-walled ducts of finite length (I):The effects of duct cross-section geometry and source distribution space-time pattern[J].Journal of Sound and Vibration,1973,31(1):1-72.

[8]Doak PE.Excitation,transmission and radiation of sound from source distributions in hard-walled ducts of finite length (II):The effects of duct length[J].Journal of Sound and Vibration,1973,31(2):137-174.

[9]Wang K S,Tszeng T C.Propagation and radiation of sound in a finite length duct[J].Journal of Sound and Vibration, 1984,93(1):57-59.

[10]郑 晗,周其斗,谢志勇.一种基于NASTRAN无限元技术的导管声学计算方法[J].海军工程大学学报,2015,27(1): 68-73. Zheng Han,Zhou Qidou,Xie Zhiyong.A calculation method for duct acoustics based on NASTRAN infinite element technology[J].Journal of Naval University of Engineering,2015,27(1):68-73.

[11]杜功焕,朱哲民,龚秀芬.声学基础[M].南京:南京大学出版社,2004.

[12]Ver IL,Beranek L L.Noise and vibration control engineering[M].USA:Wiley,2005.

Study of sound radiation of a simple duct excited by sound source

ZHENG Han1,WANGWei1,ZHOU Qi-dou2
(1.Naval Academy of Armament,Beijing 100161,China;2.Dept.of Naval Architecture Engineering, Naval Univ.of Engineering,Wuhan 430033,China)

Based on NASTRAN infinite element technology,the sound radiation of a simple duct excited by sound source was studied detailedly.The relationship between wavemode and radiated energy was founded, and the influence of the duct’s radius,length,length-to-diameter ratio on wavemode,radiated power and directivity of far field was considered.The results show that:there are two parameters that affect duct’s wavemode and radiated power,the non-dimensional wave number and the length-to-diameter ratio;and with the ratio becomes smaller,the radiated power becomes smaller,and the lateral shielding effect becomes weaker.It should be considered comprehensively to choose proper size of duct for the best effects of sound power reduction and lateral shielding；the lateral shielding effects act on high frequency band rather than low frequency band.

ductacoustics;acoustic excitation;monopole

U661.44

：Adoi:10.3969/j.issn.1007-7294.2017.02.013

2016-07-08

总装备部“十二五”预研项目（9140A14080512JB11165）

郑 晗（1988-），男，博士，工程师，E-mail:zhenghanhust@qq.com；

王 玮（1981-），男，硕士；周其斗（1962-），男，教授，博士生导师。

1007-7294（2017）02-0228-09