基于内聚力模型的X65管线钢稳定裂纹扩展研究

苗 婷，苗张木，冷晓畅

（1.武汉理工大学 交通学院，武汉 430063；2.南昌大学 建筑工程学院，南昌 330031）

基于内聚力模型的X65管线钢稳定裂纹扩展研究

苗 婷1，苗张木1，冷晓畅2

（1.武汉理工大学 交通学院，武汉 430063；2.南昌大学 建筑工程学院，南昌 330031）

断裂破坏是海工结构中主要的失效模式之一。对管线钢管的断裂韧度评定以及其裂纹扩展行为的模拟研究，对于评估管道结构的安全性、结构完整性有重要的指导意义。在众多用于模拟裂纹大变形稳定扩展的理论中，内聚力模型方法（CZM），对大范围屈服的断裂行为分析十分有效。它具有强大的物理基础以及可在数值方法中逐步实现的适应性。鉴于此，文章运用CZM模型对X65管线钢双引伸计法的断裂韧度试验进行模拟，对比计算与试验结果。研究了不同CZM模型参数对模拟结果的影响，并优化了模型。用其作为计算模拟预测X65管线钢稳定裂纹扩展行为的方法，可替代部分实验来完成可靠性评估。

内聚力模型（CZM）；双引伸计法；裂纹扩展

0 引 言

断裂破坏是海工结构中主要的失效模式之一，也是结构完整性、安全性评估研究的热点问题。油气管道作为海工结构的一种，在服役过程中，受海洋恶劣环境的影响，其结构因疲劳损伤累积易萌生裂纹。在受到较大的外载荷作用下，裂纹不断扩展导致断裂失稳，最终导致结构的破坏。裂纹损伤已成为油气管线中不可避免的损伤形式之一。因此对管线钢管的断裂韧度评定以及其裂纹扩展行为的模拟预测研究，是确保结构安全运行的关键，对于评估管道结构的安全性、完整性以及剩余强度都有重要的指导意义。

目前，用于模拟裂纹大变形稳定扩展的基础理论有很多。基于裂纹尖端张开位移（CTOD）、裂纹尖端张开角（CTOA）、J-R阻力曲线、内聚力模型(CZM)等理论的模拟方法都被广泛应用。而其中，基于CTOD以及CZM的方法，对大范围屈服的断裂行为的分析十分有效。在实际中，CZM允许沿着裂纹路径在材料周围引入界面单元，并且可以在有限元分析代码中易于实施。基于其强大的物理基础以及可在数值方法中逐步实现的适应性，可将其作为模拟预测稳定裂纹扩展行为的计算方法，替代部分实验来完成可靠性的评估。

鉴于此，本文运用双引伸计法对X65管线钢进行断裂韧性评定测试。获得材料的CTOD以及J积分等断裂参量。并在此基础上运用内聚力计算模型（CZM）模拟实验过程中的稳定裂纹扩展行为，将其与实验相结合，分析得出适用于研究分析断裂韧度测试过程中的材料扩展断裂行为的CZM模型以及相关参数。

1 断裂韧性试验

1.1 材料与试样的制备

试验所用材料为无缝钢管X65QO，其焊管规格、基本力学性能及试验温度见表1。

表1 试验材料基本参数Tab.1 Basic parameters of testmaterials

参照DNV规范[1]对管线钢断裂韧性测试试验的取样要求，以及英国规范BS7448[2]的规定，采用三点弯曲试样形式即单边缺口弯曲试样（SENB），用线切割机从钢管上截取，如图1所示。按照规范[2]要求，为了得到符合全厚度要求的SENB试样，应尽量减小管线试样的曲率。按照上述取样、加工要求，在毛坯样上进行精加工，所得试样如图2所示，尺寸为S=75.2mm，W=18.8mm，B=9.4mm（S为试样跨距，W为试样宽度，B为试样厚度）。

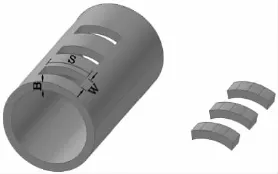
图1 管线钢取样Fig.1 The sampling position of pipelines

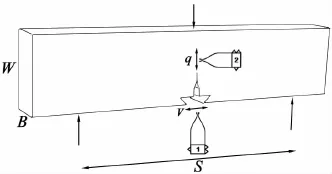
图2 试样尺寸及引伸计的安置Fig.2 Dimensions of specimens and placements of gauges

1.2 双引伸计法

本文参照文献[3]，用“双引伸计法”进行断裂韧度试验。所谓的“双引伸计法”，即运用两个引伸计同时采集一个试样上的相关位移的方法。在传统的CTOD断裂韧度试验的基础上，同时进行J积分断裂韧度的测试方法。如图2～3所示，本文采用了1号与2号两个夹式引伸计进行试验。将1号引伸计安置在试样裂纹嘴上，以测量裂纹嘴张开位移（CMOD）。与此同时，用2号引伸计测量加载线位移（LLD），即加载点（压头）的垂直位移，它的一端夹持固定在压头的刀口上，另一端则夹持在立柱的刀口上，如图3所示。这样在加载过程中，可以在一套系统中同时记录F-V曲线与F-q曲线。其记录结果如图4。其中F为荷载，V为试样裂纹嘴位置张开位移（CMOD），q为竖向载荷线位移（LLD）。

图3 双引伸计法装置Fig.3 Double gaugemethod device

图4 X-Y记录仪记录曲线Fig.4 Curves recorded by X-Y data recorders

1.3 实验过程

在制备含裂纹的试样后，进行主体试验。依照BS7448标准，使用电液伺服万能试验机，对试样按一定速率进行加载，并通过X-Y函数记录仪，记录F-V曲线以及F-q曲线。卸载后，对未脆断的试样进行二次疲劳以保护断口，压断试样观察断口形貌并测量裂纹初始长度a0和裂纹扩展量Δa，根据测量值以及曲线相关信息，结合规范[3]中（6）式与（9）式进行计算，得到CTOD以及J积分的特征值δ与J，见表2。

表2 断裂韧性试验结果Tab.2 Fracturemechanics toughness test results

2 内聚力模型准则及其参数

2.1 三角形内聚力准则

在众多研究文献中，针对不同的材料体系采用不同的内聚力准则进行研究[4]。其中，指数、三角形和梯形内聚力法则较为常用。本文采用最常用的三角形内聚力准则，即三角形张力-位移法则（traction-separate law，简称TS-Law）。

图5为三角形法则的TS关系曲线。沿直线OA段，材料在载荷作用下并未产生损伤，斜率K（界面刚度）越大，界面相对的分离位移越小。加载到达点A处（对应的分离位移δninit为初始损伤位移），内聚力达到最大值（界面应力）Tmax。之后，材料出现损伤，内聚力下降。当应力下降至零，即C点（当前裂纹尖端），此时的分离位移为δnfail，材料开裂界面完全分离，内聚能达到其最大的临界值Φ。Φ的值即为张力-位移曲线下包含的面积。

图5 三角形内聚力TS准则Fig.5 The triangular cohesive traction-separation law

对于I型张开裂纹，根据TS准则图形几何关系不难推算出关系式：

即内聚能与另外两个参数有关。因此，三个参数中任取两个可被视为CZM模型的初始输入参数。除此以外，另外一个参数则须用于描述TS准则的形状。该参数可以为界面刚度K，或者最大内聚力下对应的初始损伤位移δ。 其对应关系为：

2.2 界面刚度的取值

一系列文献研究表明界面刚度的取值方法各不相同。文献[5]依照界面的尺寸以及材料的弹性模量来计算界面刚度。而文献[6]则根据自身试验提出界面刚度范围为每单位长度上104～107倍的界面应力。文献[7]提出了K＞＞E/L的概念，而文献[8]则给出了相关的计算式：

式中：t表示邻近的界面层厚度，E3为垂直于界面宽度方向的材料弹性模量。α为远大于1的系数（α＞＞1）。

2.3 内聚力（界面应力）的取值

内聚力即界面应力Tmax的取值，在各类CZM模型中通常是基于内聚区材料的屈服强度σs，有时则与材料的抗拉强度σb相关。在各类文献研究中，文献[8]总结了界面应力与屈服强度的比值Tmax/σs为1.2～4的不同情况，最终选择了2σs为其在CZM模型计算中的取值。文献[7]对Ⅰ型裂纹的稳定扩展运用CZM模型进行了一系列模拟。在模拟预测与实验结果对比中，最终发现Tmax=2.2σs时，模拟的载荷-裂纹扩展曲线与试验结果相吻合。

2.4 内聚能的取值

一般认为，内聚能等于断裂能G，即形成完全断裂面所消耗的能量[7]，也就等于 T-S曲线所围成的面积。而断裂能的试验方法与计算方法在不同文献中也不尽相同。有研究认为Gc与Jc相关[10]，而间接取得Jc的方式有很多。例如本文1.2节中运用双引伸计法通过实验测得J积分的取值。除此之外，根据文献[11]，基于断裂力学理论，可以运用试验测得的裂纹尖端张开位移CTOD值来换算JIC从而取得内聚能。J积分与CTOD的关系如下：

通过有限元计算与实验相结合得到，约束因子m取1.7时较为合适。另外，文献研究表明相较于σs用σflow来应用于CTOD与Jc的关系更为合适。其中：

文献[3]曾提出裂纹尖端张开位移CTOD与表征能量的积分之间存在某种线性关系，并指出规范[1]就曾建议两者的关系式为：

3 有限元模拟

3.1 X65钢管的裂纹扩展CZM建模

本文运用ABAQUS软件以及自编译子程序[8]对X65管线钢断裂韧度测试试样的加载和变形情况进行有限元模拟。利用CZM模型，模拟预测试样裂纹的稳定扩展情况。模拟采用3D划分网格体现。如图所示，试样采用C3D8R单元划分，而内聚区则通过生成一层厚度为零的CZM内聚力层来实现。该层CZM单元设置在Ⅰ型断裂路径上，起始于裂纹启裂前沿（预制疲劳裂纹前沿），沿试样宽度方向终止于试样边缘。本文取试样厚度方向上8个层面；裂纹扩展方向上，内聚力单元尺寸0.2mm进行计算模拟。图6～7为试样的ABAQUS有限元建模以及应力分析结果。

图6 对试样进行3D划分网格Fig.6 A 3Dmesh for the specimen

图7 裂纹扩展的应力云图Fig.7 Stress nephogram of crack extension

3.2 内聚力参数的选择计算

由于CZM参数很难通过实验测得，而且没有建立完善的准则来进行估算，其值通常通过尝试来得到。为了最终选取合适的参数对裂纹扩展进行模拟，则须考虑所有取值情况进行计算模拟以及实验对比。对内聚能、界面应力以及界面刚度的取值如表3所示。

表3 内聚能与界面应力取值Tab.3 Values of cohesive energy and interface stress

对于界面刚度根据公式（3），取α=50，内聚力单元几何厚度为0.01 mm，则计算出K=1.05×109N/ mm3。模拟过程中取为K=109N/mm3。

3.3 试验与模拟结果

将表3中的取值两两组合，K不变，得到共9组数据（见表4），取试样X65-1进行数值计算。比较模拟结果与试验结果的载荷-载荷线位移曲线（F-q曲线），结果如见图8所示。

表4 X65管线钢数值模拟的模型参数以及算例编号Tab.4 M odel parameters of numerical simulation for X65 pipeline steel and exam p le numbers

图8中可以看出，算例SP103曲线与试验结果的F-q曲线最为吻合。断裂能与界面应力对F-q曲线进入最大载荷平台点的位置以及裂纹扩展后，载荷变化趋势都有一定的影响。当内聚力为2.2σs，断裂能为试验测得的J积分特征值时，可以得到与实验相对吻合的计算结果。

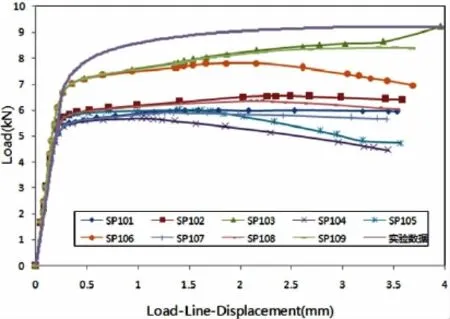
图8 不同组合下F-q曲线与试验结果对比Fig.8 Comparison of F-q curves in different combinations from experiments and simulations

4 计算与实验结果的对比讨论

4.1 界面刚度对模拟结果F-q曲线的影响

取SP103算例中的内聚力与内聚能的值固定不变，根据2.2节对K的取值介绍，分别取K=103N/mm3，104N/mm3，106N/mm3，109N/mm3，1012N/mm3进行计算模拟。结果如图9所示。

不难看出当内聚能、界面应力一定时，计算结果F-q曲线的线弹性形变阶段的斜率由界面刚度K决定。当K达到一定值之后（106N/mm3），F-q曲线斜率逐渐趋于一致，此时K对斜率的影响不再重要。因此在模拟预测X65管线钢裂纹扩展时，取K≥106N/mm3即可。

4.2 内聚能与界面应力对模拟实验结果的影响

根据算例SP103对CZM参数的取值，分别保持Φ=847 kJ/mm2，Tmax=1 056 MPa不变，对比计算结果曲线，如图10所示。

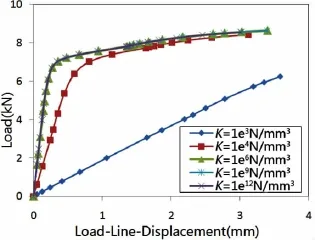
图9 界面刚度对模拟结果的影响Fig.9 The influence of interface stiffness on simulate results

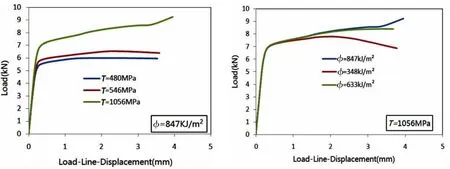
图10 不同界面应力、不同内聚能的F-q曲线模拟结果Fig.10 Simulation results of F-q curves for various values of interface stress and cohesive energy

从图中不难看出，当CZM参数中内聚能相同时，界面应力的不同导致F-q曲线进入最大载荷平台载荷值不同。三条曲线呈现高低不同的态势。即裂纹稳定扩展阶段的最大载荷不同。可见，F-q曲线的高度是由界面应力的大小决定。

而当界面应力一致时，F-q曲线的斜率以及进入裂纹扩展阶段的初始载荷是一致的。当裂纹扩展到一定程度，后期的损伤软化过程则受内聚能的影响而有所不同。内聚能越大，末端的载荷值越大，曲线呈上扬趋势。内聚能越小，末端的载荷值越小，曲线呈下降的趋势。简而言之，内聚能的大小决定了F-q曲线的“胖瘦”。

4.3 CZM各参数的改进优化

在界面刚度K保持不变的基础上调整内聚能和界面应力，适当增大两者的数值以期更好地与实验结果曲线相吻合。

在此过程中，先保持Tmax=1 056MPa不变，取较大的内聚能进行尝试。结果发现当Φ达到J积分及其以上之后，对曲线的走势影响甚微。而且无规律可循，不再呈单一趋势影响。另外内聚能过大还会导致有限元计算过程中的多次迭代，从而造成计算结果的不收敛。

保持内聚能与界面刚度不变，适当提高界面应力数值进行模拟。即Φ=847 kJ/m2，分别取Tmax=2.2σs，2.7σs，3σs，3.5σs，3.6σs进行计算模拟。结果如图11所示。

图11 不同界面应力的F-q曲线计算结果Fig.11 Simulation results of F-q curves for various values of interface stress

图12 X65-1试样F-V曲线模拟结果对比Fig.12 Comparison of F-V curve for X65-1 from experiments and simulations

图11中的F-q曲线结果对比显示，当Tmax=2.2σs时，其对应曲线的最大载荷平台略低于其他模拟结果。而当增加到2.7σs，界面应力提高曲线平台的优势逐渐表现得不明显。其影响敏感性降低，之后界面应力的增大对载荷走向趋势影响甚微。因此，在CZM模型计算中取Tmax=2.7σs作为分析X65管线钢裂纹扩展的计算模拟方法。

4.4 内聚力模型模拟结果验证

通过以上研究，获得了计算模拟X65管线钢的裂纹扩展的CZM模型。为了证明此模型的普遍适用性。在计算结果中提取F-V曲线与实验结果对比，观察是否适用于CTOD断裂韧性试验。另外将该模型应用于其他试样，以判断之前的对比结果是否存在偶然性（图12）。

从对比结果发现，对于X65-1试样，用优化后的CZM模型模拟的F-V曲线结果与实验数据在线弹性阶段相吻合，保持基本一致的斜率。弹塑性阶段较吻合，最大载荷平台在后期达到一致。其模拟的F-V曲线形状与F-q曲线相似。

用相同的模型模拟X65-2试样，无论是J积分试验还是CTOD试验曲线，在线弹性阶段吻合情况良好。而不同于X65-1，在试验进入弹塑性阶段，裂纹开始稳定扩展后，模拟结果的最大载荷平台略高于实际实验数据。其后期曲线末端走势与试验结果较吻合。

图13 X65-2试样的CZM模拟结果对比Fig.13 Comparison of experimentalmeasurements and simulation predictions using CZM for X65-2

5 结论与讨论

本文结合断裂韧性测试试验以及内聚力模型模拟计算方法，对X65管线钢稳定裂纹扩展行为进行研究，得到以下结论：

（1）改良传统的CTOD断裂韧度评定试验，运用“双引伸计法”，通过增加一套引伸计设备，在获得CTOD相关参量结果的同时，同步研究了J积分的相关参数。优化了断裂韧度评定试验方法，为模拟裂纹扩展断裂行为提供了多样化的参考因素。

（2）通过对比各组模拟结果的F-q曲线，并结合试验结果，得到了CZM参数对裂纹扩展行为计算结果的影响规律与程度。即内聚力模型的界面应力决定了F-q曲线最大载荷平台的高度，内聚能决定了F-q曲线末端走向，以及整个曲线的形状，而裂纹发生损伤前的线弹性形变阶段的斜率则由界面刚度K决定。

（3）对比模拟结果与试验结果，深入研究CZM各参数对裂纹扩展模拟结果的影响，得到更为具体的参数选取标准。即界面应力值控制在2.2～2.7σs为佳。内聚能应取与J积分相等的值，其值过小导致试验后期的损伤软化过快，过大则造成计算结果的不收敛。界面刚度按照公式（3）计算较为合适，当其值增加到一定程度，其对曲线斜率的影响程度也随之下降，敏感度降低。

（4）通过同样的CZM参数值设置方法，对裂纹扩展行为进行模拟。所模拟预测的F-V曲线与实验结果相吻合。从而提供了一种结合CZM模型与J积分参量来模拟裂纹扩展行为以预估CTOD值的方法。运用CZM模型计算模拟可以部分替代试验完成结构的可靠性评估。

（5）运用优化的CZM模型计算模拟同类材料试样X65-2的裂纹扩展行为。对比F-q、F-V曲线的计算结果与试验结果，发现参数选择过程中内聚能的选取较为准确。而针对界面应力值的选择，虽然在一定范围内其模拟的曲线形状与实际情况相仿，但对最大载荷平台的影响有待深入研究，其计算结果的最大载荷平台相对于实际曲线，上下浮动，并不能很好地吻合。这说明单纯用特定相关于σs的界面应力参数确定曲线最大载荷平台的方法有待完善。具体系数的取值有待进一步研究。

[1]Offshore Standard.DNV-OS-F101:Submarine Pipeline Systems[S].2010.

[2]BS7448:Part1:Fracturemechanics toughness tests-Method for Determination of KIC、Critical CTOD and Critical JValues of Metallic Materials[S].London:British Standard Institution,1991.

[3]苗张木.厚钢板焊接接头韧度CTOD评定研究[D].武汉:武汉理工大学,2005.

[4]Chen Xin,Deng Xiaomin,An inverse analysis of cohesive zonemodel parameter values for ductile crack growth simulations[J].International Journal ofMechanical Sciences,2014,79:206-215.

[5]Daudeville L,Allix O.Delamination analysis by damagemechanics:Some applications[J].Composites Engineering,1995, 5(1):17-24.

[6]Zou Z,Reid SR,Li S.Modelling inter laminar and inter laminar damage in filamentwound pipes under quasi-static indentation[J].Journal of Composite Materials,2002,36:477-499.

[7]Chen X.Numerical study of stable tearing crack growth events using the cohesive zonemodel approach[D].South Carolina:University of South Carolina,2013.

[8]Travesa A T.Simulation of delamination in composites under quasi-static and fatigue loading using cohesive zonemodels [D].Girona:Universitat De Girona,2007.

[9]LiW,Siegmund T.An analysis of crack growth in thin-sheetmetal via a cohesive zonemodel[J].Eng Fracture Mechanics,2002,69(18):2073-2093.

[10]Shet C,Chandra N.Analysis of energy balance when using cohesive zonemodels to simulate fracture processes[J].Journal of Engineering Materials and Technology,2002,124:1-11.

[11]Fracture and fatigue control in structures:Applications of fracturemechanics[M].ASTM International,1999.

Study of stable crack grow th through X65QO pipeline steel using cohesive zonemodeling

MIAO Ting1,MIAO Zhang-mu1,LENG Xiao-chang2
(1.School of Transportation ofWuhan University of Technology,Wuhan 430063,China;2.School of Civil Engineering and Architecture of Nanchang University,Nanchang 330031,China)

Fracture failure is one of themajor failuremodes in offshore structures,whichmakes the assessment of fracture toughness and the investigation of crack growth on pipeline steels great significance on evaluating the safety and structure integrity.Among themany theories for simulation of a large scale crack extension,the cohesive zonemodel(CZM)is very efficient on analyzing fracture events in the condition of large-scale yielding.It has strong physics basis and ease in numerical implementation.Therefore,in this paper,the CZM is utilized to simulate the fracture toughness test of X65 pipeline steel,which is processed by‘Double Gauge Method’.By comparing the simulation results and the experimental results,the influence of variables in CZM is investigated and the CZM for the simulation and prediction of X65 pipeline steel stable crack growth is improved.By using the improved CZM,a portion of the experiment can be substituted by simulation in safety assessment.

cohesive zonemodel;Double Gauge Method;crack growth

U661.72

：Adoi:10.3969/j.issn.1007-7294.2017.02.009

2016-10-09

苗 婷（1987-），女，博士研究生，E-mail:miaoting1615@hotmail.com；

苗张木（1957-），男，教授，博士生导师。

1007-7294（2017）02-0192-09