基于角速率匹配法的船体变形实船测量技术研究

史宏洋，尤太华，张义，高伟

（1．北京航天自动控制研究所，北京100854；2.哈尔滨工业大学，哈尔滨150001）

基于角速率匹配法的船体变形实船测量技术研究

史宏洋1，尤太华1，张义1，高伟2

（1．北京航天自动控制研究所，北京100854；2.哈尔滨工业大学，哈尔滨150001）

针对船体变形测量技术大多处于理论仿真的局限性，提出了基于实船试验的船体变形测量技术，考虑到测量速度的需要及静态变形角缓慢变化的特征，推导了基于角速率匹配法“准静态”模型。采用Kalman滤波技术对Mochalov模型和“准静态”模型下的变形角进行了估计，从实船试验的角度验证了船体变形的产生原因，拓展了“准静态”模型适用范围，进一步分析了舵操作对船体变形角的影响。试验结果表明，“准静态”变形角对缓变静态变形角跟踪效果良好，提高了静态变形角的测量精度，为光纤陀螺船体变形测量技术的实际应用奠定了坚实的基础。

船体变形；Mochalov模型；舵操作；“准静态”

0 引言

现代舰船一般都装备有雷达系统、光学瞄准系统、跟踪系统、导弹发射系统及导航系统等[1]，这些系统之间的通信及高质量的协作必须在统一的坐标基准下才能完成。由于船体变形的存在，使得舰船上相关设备协调工作所用的坐标基准不再统一，这严重影响了设备性能的发挥，降低了精度[2-4]。为了克服船体变形的影响，近年来，国内外学者纷纷致力于船体变形的测量与补偿技术。相比较而言，惯性测量匹配法由于可以进行全天候实时精确的测量[5-6]而备受青睐，俄罗斯圣彼得堡“电气仪表厅”和“电工大学”自20世纪80年代末期首先开展了对这方面的研究[3-4]，在此基础上，美国、澳大利亚、韩国和波兰也相继展开了相关研究[7-12]，国内的研究虽然起步较晚，但仍然取得了一定的成果[13-18]。

俄罗斯学者Mochalov在文献[6-7]中分析了船体产生变形的原因并给出了变形角的分类与定义，但是并没有从实船试验的角度来验证影响船体变形的产生因素，同时忽略了静态变形角缓慢变化的特性。文献[14]针对静态变形角缓慢变化的特征提出了“准静态”模型，但是只对该模型进行了理论仿真验证，并没有进一步进行实船试验验证。文献[15]提出了一种基于姿态匹配法的船体变形测量技术，虽然该方法与角速率匹配法相比精度较高，但是对于实船试验来说，其测量速度较慢。

本文针对船体变形测量技术大多处于理论仿真的局限性及测量速度的需要，采用可以进行全天候实时精确测量的惯性测量匹配法中的角速率匹配法，从实船试验角度对先验Mochalov变形模型进行分析和验证，进而对船体形变的产生原因进行分析总结。为了进一步分析舵操作对船体变形角的影响，建立了“准静态”模型下的观测方程和量测方程，并对该模型进行了实船试验和分析。

1 角速率匹配法原理

光纤陀螺测量船体形变角的原理如图1所示，将两个光纤陀螺单元（Fiber Gyro Unit，简称FGU）分别安装在船体的中间和船头二个位置（分别为FGU1和FGU2）。如果FGU1和FGU2之间没有变形角时，两个坐标系平行，如果有形变角时，两个坐标系将不平行，那么光纤陀螺三个轴敏感到的横摇、纵摇和航向角速度也不相等，通过测量其角速度之差来对静态或“准静态”变形角和动态变形角进行估计。

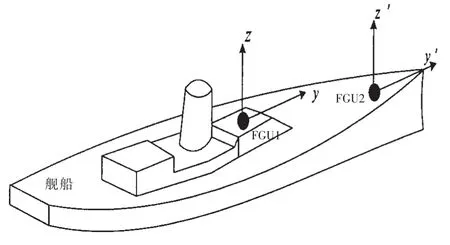
图1 光纤陀螺的安装示意图Fig.1 The installation schematic figure of fiber optic gyroscopes

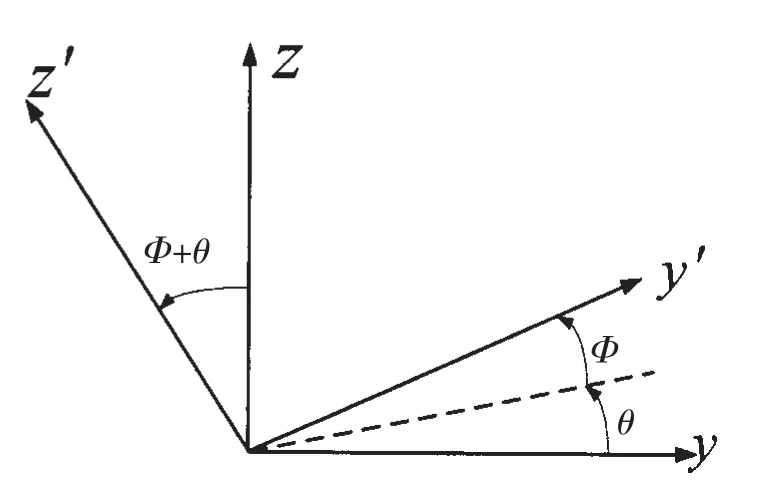
图2 变形角示意图Fig.2 The schematic diagram of ship’s deformation

FGU1与FGU2的三个轴均与船体固联，以FGU1为例，其oy轴指向船体的纵向，oz轴垂直于甲板平面指天，ox轴的取向由其它两个轴通过右手定则来确定。假设这两个光纤陀螺FGU1和FGU2的失准角由两部分组成：一部分是静态或“准静态”变形角Φ，另一部分是动态变形角θ，则总变形角为φ=Φ+θ，如图2所示。

对于Mochalov形变模型，文献[6]已经给出了详尽的推导过程，这里将直接采用。所以本文只对“准静态”模型进行推导。

设FGU1测得的船体的绝对角速度在oxyz上的投影为Ω1，而FGU2测得的船体的绝对速度在ox′y′z′上的投影为Ω2，那么：

由文献[6]可得，陀螺FGU1与FGU2之间的角速率差为：

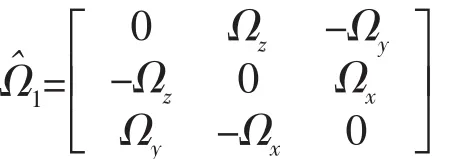
2 卡尔曼滤波方程的建立

采用卡尔曼滤波估计时，其量测方程写成矩阵的形式为：

其中：z是量测量，H为量测矩阵，x为状态向量，v为由量测误差形成的列矩阵（即为噪声矩阵）。

如果考虑陀螺漂移，那么：

这里D1为FGU1的陀螺漂移，D2为FGU2的陀螺漂移。由于陀螺漂移既有常值分量又有随机分量，那么（4）式可以表示为：

考虑“准静态”形变角时，状态向量可表示为：

其中：i=x，y，z。

量测矩阵即可表示为：

由于船体的静态变形角并不是一个常值，而是一个缓慢变化的过程，故可将其视为“准静态”角形变的范畴[12]。

准静态变形角模型为：

其中：τi为相关时间，w（）t为白噪声。

动态变形角模型为：

陀螺随机漂移的模型为：

其中：i=x，y，z，μi′为不规则系数，σi为系数。

由此可得系统的状态方程为：

3 基于实船试验的船体测量技术

本次试验采用试验室自研的光纤航姿设备作为测量单元，试验地点为青岛某海域，其部分主体仪器实物图如图3所示。

图3 试验中部分主体仪器实物图Fig.3 Actual objects’diagram of partial main instruments in experiments

3.1 Mochalov模型中参数λ的验证

为了更好地验证Mochalov模型中动态变形角的主频率是否选择正确，我们选取航行状态下的实船数据作为研究对象。首先对三个轴向的变形角进行频谱分析，结果见图4所示。

由图4中可以看出三个轴向的动态变形角的频率虽然会出现多个尖锋，但是在频率为0.1时三个轴向的尖锋均达到最大值，由此可见，三个轴向的动态变形角的变化主频率选择为0.1是正确且合理的。

3.2 基于Mochalov模型的实船验证及分析

为了分析引起船体变形的原因，我们分别对漂泊、锚泊和航向状态下的实船试验进行了仿真分析。3.2.1漂泊状态下的实船验证及分析

漂泊状态下，舰船的变形角参照Mochalov提出的模型，即静态变形角为常值，动态变形角模型参照（14）式所示的二阶马尔科夫过程（其中μi=0.02，λi= 0.01），由此得到的变形角如图5（a）和5（b）所示。

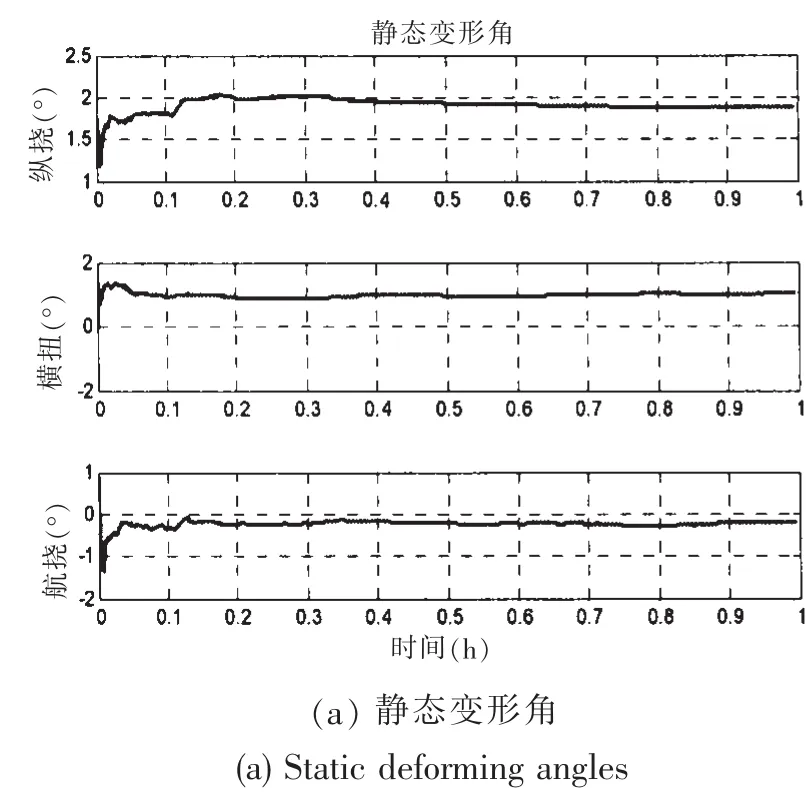
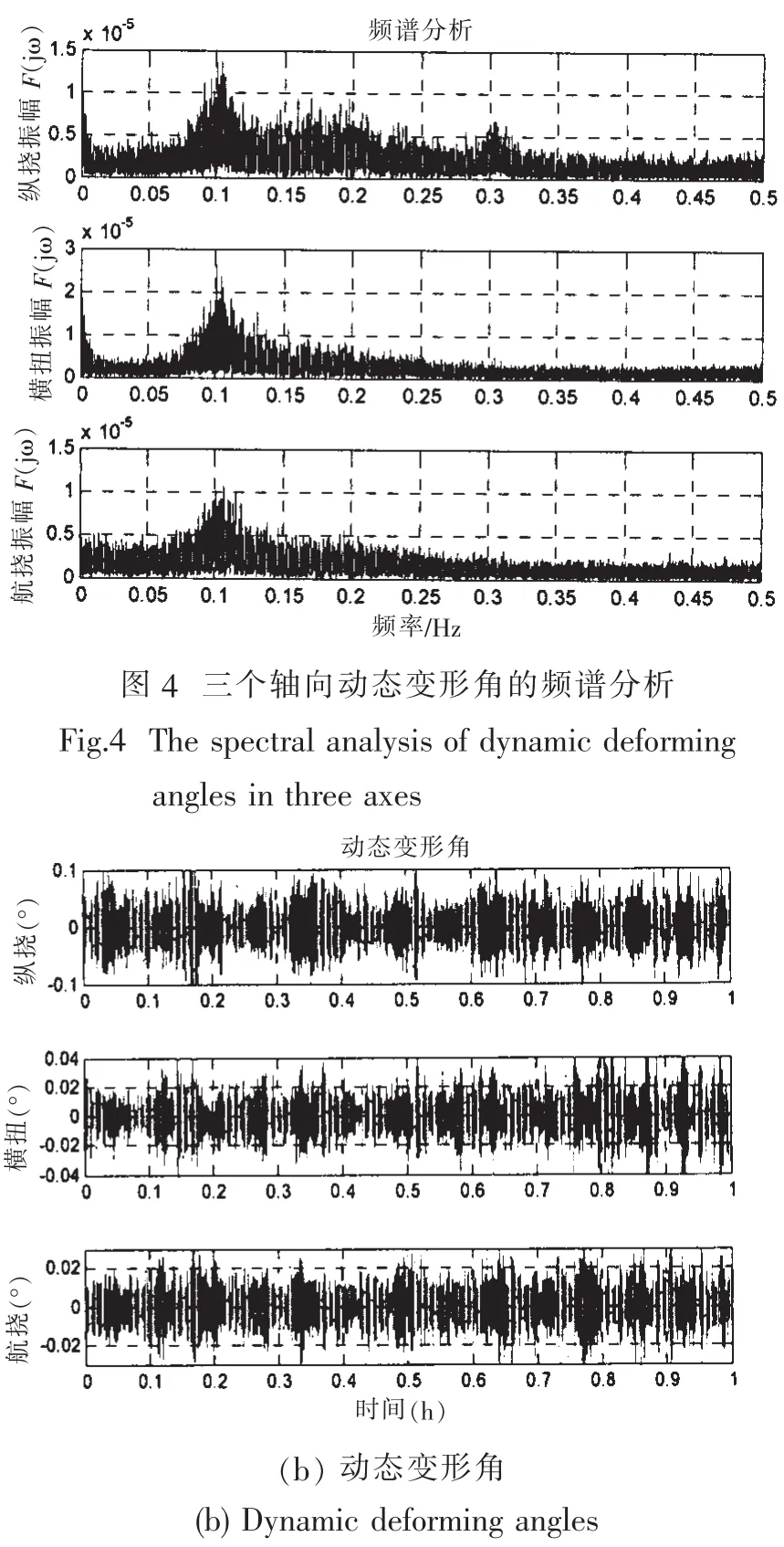
图5 漂泊状态下舰船的变形角Fig.5 The ship’s deforming angles under the state of drift

3.2.2 锚泊状态下的实船验证及分析

锚泊状态下，舰船的变形角的模型与漂泊状态下的相同，由此得到的变形角如图6（a）和6（b）所示。

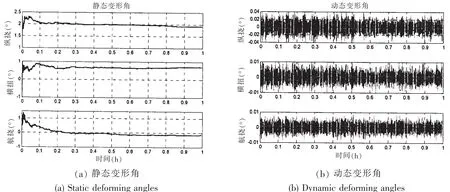
图6 锚泊状态下舰船的变形角Fig.6 The ship’s deforming angles under the state of anchoring

从图5（a）和图6（a）中可以看出，舰船在锚泊和漂泊状态下的静态变形角在滤波稳定后并不是一成不变的，而是存在一定的波动，虽然两种状态下的波动存在一定的差别，但其走向是一致的且大小几乎相等，这就说明在锚泊和漂泊状态下，引起船体静态变形角的因素是几乎相同的：即在一天内，由于载荷的变化和阳光下舰船受热的不均匀造成的。

从图5（b）和图6（b）中可以看出，在漂泊和锚泊状态下船体动态变形角较小，这是由于舰船在漂泊和锚泊状态下，不存在机动扰动和舵操作，而仅仅只受到海浪冲击等的影响，所以其动态变形角幅值就相对较小。但是比较图5（b）和图6（b）可知，漂泊状态下的动态变形角要大于锚泊状态下的动态变形角，这是由于在锚泊状态下，舰船受波浪的影响作用较漂泊时小。同时为了更进一步验证舰船的航向变化对动态变形角的影响，以锚泊状态为例，其航向变化过程如图7所示。

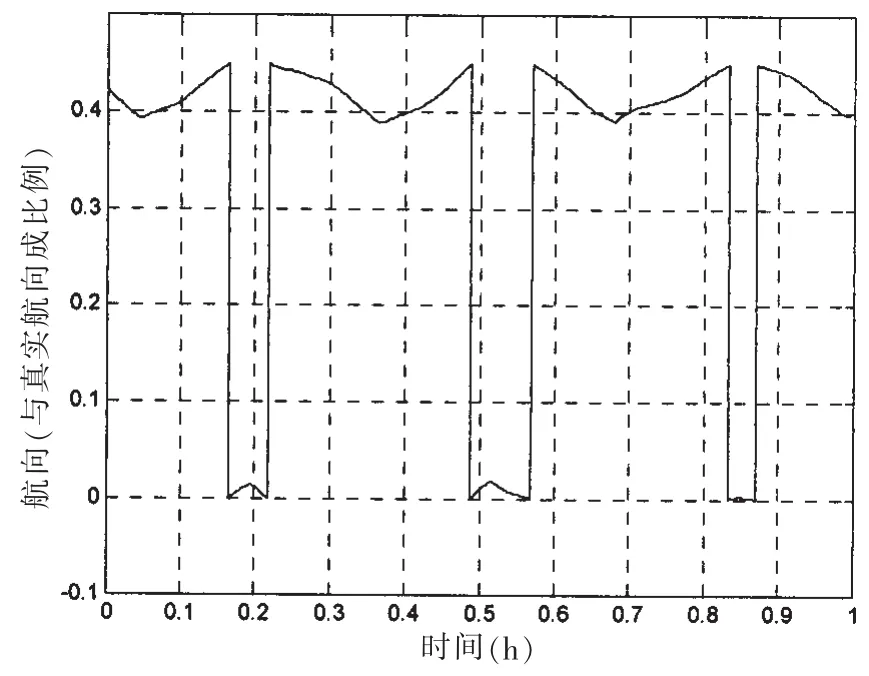
图7 锚泊状态下舰船的航向Fig.7 The ship’s heading under the state of anchoring

由图7可知，在锚泊状态下，由于在一小时内海浪的流向及风向均可认为是固定方向的，所以舰船的航向会呈现周期的变化，但是舰船并没有进行舵操作，由图6（b）可知，锚泊状态下的动态变形角的波动比较均匀，这就说明在没有舵操作下的航向变化对动态变形角并不产生影响。

由此可见，舰船在漂泊和锚泊状态下，Mochalov的模型是可行的，同时也验证了静态变形角和动态变形角的产生原因。为了更进一步地说明舵操作对动态变形角的影响，下面将针对含有舵操作的航行状态进行分析。

3.2.3 航行状态下的实船验证及分析

航行状态下（存在舵操作），当舰船的变形角的模型参照Mochalov模型时，得到的变形角如图8（a）和8（b）所示。

图8 航行状态下舰船的变形角Fig.8 The ship’s deforming angles under the state of sailing

比较图8（a）和图5（a），图6（a）可见，航行状态下静态变形角的波动要小于漂泊和锚泊状态下，这是由于在航行状态下，由于存在舵操作，即舰船具有转向运动，那么阳光的照射作用便不再只针对舰船的某一个方位，而是比较均匀，同时在航行过程中，载荷的分布几乎不发生变动，所以其波动很小。

比较图8（b）和图5（b），图6（b）可知，在航行状态下，舰船的动态变形角存在较大的波动，为了验证其与舵操作下航向的关系，在图8（b）中引入了航向（与真实航向成相应的比例），通过图8（b）可知，当航向变化时，动态变形角的幅值会相应地变大，周期相应地变长。但是在时刻0.26 h和0.55 h，由于其航向是由0°变为360°，即航向并未发生改变，所以动态变形角并没有发生波动。

3.3 基于“准静态”模型的实船验证及分析

考虑到静态变形角的波动特性及舵操作对动态变形角的影响形式，本文基于文献[15]提出的“准静态”模型，采用角速率匹配法，由此得到的“准静态”变形角如图9所示，由图中可知，当航向变化时，“准静态”变形角的波动幅度较大，当航向稳定后，准静态变形角的波动幅值也会相应地减小，但其波动围绕着某一常值。所以，总的来说，“准静态”模型能够较好地跟踪静态变形角的缓慢的变化过程，且对由舵操作引起的慢变过程也具有较好的跟踪作用，从而提高了“准静态”变形角的测量精度，进而提高了舰船上相应导航系统性能的发挥。由图中“准静态”变形角复杂的波动情况可以看出，除了舵操作，阳光照射和负载变化的影响因素外还有其他未知的影响因素，这就需要进一步进行试验验证。

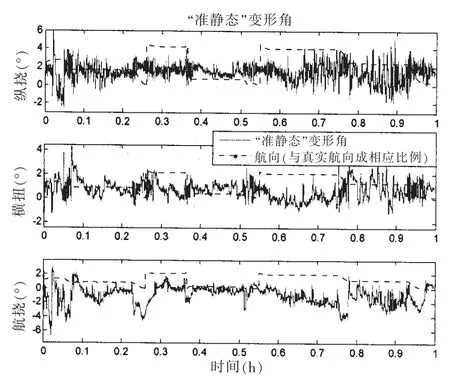
图9 航行状态下舰船的“准静态”变形角Fig.9 The ship’s‘quasi-static’deforming angles under the state of sailing

4 结论

针对目前船体变形测量技术大多处于理论仿真阶段的局限性，本文基于自研的光纤航姿设备在青岛某海域进行了实船试验。考虑到实船试验的测量速度和静态变形角缓慢变化的特征，推导了角速率匹配法下的“准静态”模型。用卡尔曼滤波分别对Mochalov模型和“准静态”模型下的变形角进行了估计，得到的结论如下：

（1）通过对实船数据进行频谱分析，验证了Mochalov模型中动态变形角主频率选择为0.1的正确性。

（2）通过漂泊和锚泊状态下实船测量得到的变形角曲线验证了舰船的静态变形角和动态变形角的影响因素。

（3）通过结合锚泊状态下的航向变化曲线，可以得出在没有舵操作情况下的航向变化并不对舰船的动态变形造成影响。

（4）通过航行状态下的实船测量验证了舵操作下的航向变化会对舰船的动态变形产生影响，且在舵操作期间动态变形角的幅值会增大，周期变长。

（5）对航行状态的实船数据引入“准静态”模型后，得到的“准静态”变形角可以较好地跟踪静态变形角缓慢变化的过程，从而提高了测量精度。为光纤陀螺船体形变测量技术的实际应用奠定了坚实的基础。

[1]黄昆,单福林,杨功流,刘玉峰．舰载角速度匹配传递对准方法研究[J]．中国惯性技术学报,2005,13(4)：l-5．Huang Kun,Shan Fulin,Yang Gongliu,Liu Yufeng.Attitude plus angular rate matching method for shipboard transfer alignment[J].Journal of Chinese Inertial Technology,2005,13(4)：l-5．

[2]Ma X,Qin S,Wang X,et al.Measurement of ship deformation based on ARX model[C]//Selected Proceedings of the Chinese Society for Optical Engineering Conferences held November 2015.International Society for Optics and Photonics, 2016：97961G-97961G-7.

[3]Wei G,Wei S,Bo X,et al.Nonlinear deformation measurement method based on IMU for ship[C]//2015 IEEE International Conference on Mechatronics and Automation(ICMA).IEEE,2015：1397-1401.

[4]Dai H,Lu J,Guo W,et al.IMU based deformation estimation about the deck of large ship[J].Optik-International Journal for Light and Electron Optics,2016,127(7)：3535-3540.

[5]朱昀炤,汪顺亭,缪玲娟,葛远声．船体变形测量技术综述[J]．船舶工程,2007,29(6)：58-61．Zhu Yunzhao,Wang Shunting,Miao Lingjuan,Ge Yuansheng.Review of measuring technique for ship deformation[J].Ship Engineering,2007,29(6)：58-61．

[6]Mochalov A V.A system for measuring deformation of large-sized objects[C]//RTO/NATO.France,1999,15.1-15.9.

[7]Mochalov A V,Kazantsev A V.Use of ring laser units for measurement of the moving object deformations[C].Proceeding of SPIE,Vol.4680,2002：85-92.

[8]Dr Dana L,Day Lockheed Martin.Measuring structural flexure to improve precision tracking[R].ADA364862,1999.

[9]Milner H R,Peczkis Jan.Wooden ship hulls as box girders with multiple interlayer slip[J].Journal of Structural Engineering,2007：855-861.

[10]Lyou Joon1,Lim You-Chol.Transfer alignment considering measurement time delay and ship body flexure[J].Journal of Mechanical Science and Technology,2009,23：195-203.

[11]Lyou Joon1,Lim You-Chol.Transfer alignment error compensator design based on robust state estimation[J].Trans.Japan Soc.Aero.Space Sci,2005,161(48)：143-151.

[12]Murawski Lech.Shaft line alignment analysis taking ship construction flexibility and deformations into consideration[J].Marine Structures,2005,18：62-84.

[13]Shi Lei,Yue Dongxin,Song Xigeng.Research on shafting alignment considering ship hull deformations[J].Marine Structures,2010,23：103-114.

[14]郑佳兴,秦石乔,王省书．基于姿态匹配的船体形变测量方法[J]．中国惯性技术学报,2010,18(2)：175-180．Zheng Jiaxing,Qin Shiqiao,Wang Xingshu.Attitude matching method for ship deformation measurement[J]．Journal of Chinese Inertial Technology,2010,18(2)：175-180．

[15]郑佳兴,秦石乔,王省书．考虑准静态缓变量的船体角形变测量[J]．中国惯性技术学报,2010,18(2)：175-180．Zheng Jiaxing,Qin Shiqiao,Wang Xingshu.Ship hull angular deformation measurement taking slow-varying quasi-static component into account[J]．Journal of Chinese Inertial Technology,2010,18(2)：175-180．

[16]Salman Majeed,Fang Jiancheng.Comparison of INS based angular rate matching methods for measuring dynamic deformation[C].The Ninth International Conference on Electronic Measurement&Instruments,2009：332-336.

[17]Salman Majeed,Fang Jiancheng.Performance improvement of angular rate matching shipboard transfer alignment[C].The Ninth International Conference on Electronic Measurement&Instruments,2009：706-711.

[18]Zhou Weidong,Ding Guoqiang,Hao Yanling,Cui Guangzhao.Research on the effect of ship’s deck deflection on angular rate matching based transfer alignment process[C].Proceedings of the 2009 IEEE International Conference on Mechatronics and Automa,2009：3218-3222.

Actual ship measurement technology research of ship deformation based on angular matching method

SHI Hong-yang1,YOU Tai-hua1,ZHANG Yi1,GAO Wei2
(1.Beijing Aerospace Automatic Control Institute,Beijing 100854,China; 2.Harbin Institute of Technology,Harbin 150001,China)

In order to solve the limitation of ship deformation measurement technologies on the basis of theory simulation phases,a measurement technology based on actual ship test was proposed.Considering the measurement speed and the slowly varying feature of static deforming angle,‘quasi-static’model was put forward.Kalman filter was used to estimate the ship’s deforming angles based on the model proposed by Mochalov and‘quasi-static’model respectively,and hence the reasons of ship deformation were validated from the actual ship experiments.The applicable scope was expanded,and the influence of rudder operation on ship’s deformation angles was further analyzed.The experiment results indicated that the‘quasistatic’deforming angle can track the adagio process of static deforming angle well,thus further improving the measurement accuracy of‘quasi-static’deforming angle and laid a solid foundation for the actual application of optical fiber gyro in ship deformation measurement technology.

ship deformation;Mochalov model;rudder operation;‘quasi-static’

TN967.2

A

10.3969/j.issn.1007-7294.2017.04.007

1007-7294（2017）04-0429-08

2016-04-02

国家自然科学基金项目（51379042，51179039，61203225）

史宏洋（1987-），女，工程师，E-mail：shihongyang1987@163.com；尤太华（1979-），男，高级工程师，E-mail：zld113@sohu.com。