基于MFS无网格方法的船舶耐波性预报

封培元，马宁，顾解忡

（1.中国船舶及海洋工程设计研究院，上海200011；2.上海交通大学船舶海洋与建筑工程学院，上海200240）

基于MFS无网格方法的船舶耐波性预报

封培元1，马宁2，顾解忡2

（1.中国船舶及海洋工程设计研究院，上海200011；2.上海交通大学船舶海洋与建筑工程学院，上海200240）

文章提出了一种新的基于MFS法（Method of Fundamental Solutions，即基本解法）的求解船舶势流问题的无网格数值方法。该方法采用势流控制方程的基本解表达流场中的速度势，可以得到任意阶连续的速度势导数；另外，通过引入流场虚边界的概念避免了传统边界元方法中存在奇点的问题。相比传统的边界元方法，MFS法具有无奇性、不依赖网格、不涉及数值积分、数学原理简单和算法易于编程实现的优势。文中对于MFS法在求解浅水二维剖面水动力系数中的应用进行了探索，提出了一套实用的数值算法，并进一步结合频域切片法计算了Wigley船体的垂荡和纵摇响应，通过和频域面元法及试验结果的对比验证了方法的正确性和实用性；最后应用开发的程序分析了不同水深和航速对于耐波性的影响。该研究开创性地将MFS方法应用到了船舶水动力研究领域，为之后更深入广泛地应用这一特性优良的数值方法提供了有益的参考。

MFS；无网格；切片法；势流；耐波性

0 引言

忽略流体粘性的势流模型在船舶水动力学研究中有着广泛的应用，其核心是求解不同边界条件下Laplace方程的解。由于船舶水动力研究中自由面、物面和无穷远辐射边界条件的复杂性，使得寻求解析解变得困难重重，一般情况下需要借助数值方法来进行求解。目前，以Hess和Smith[1]在1964年提出的面元法应用最为广泛，其基本原理是将物面离散为源强为常数的面元，再选取满足自由面和无穷远辐射条件的复杂格林函数根据格林公式进行数值积分得到物面上的源强分布，最后计算出物面压力分布从而得到附加质量等水动力系数。该方法的优点是鲁棒性强，可以针对任意形状的物体进行计算；但也存在一些限制，比如：（1）三维计算中涉及繁琐的物面网格生成；（2）假定物面速度势为常数后速度势的导数不连续，因而在计算二阶力时容易导致发散；（3）面元分割改变了物面几何形状，因此物面边界条件只能得到近似满足；（4）对格林公式进行积分时存在奇点问题，需要特别处理，因而增加了编程的难度。

相比而言，若采用无网格的数值方法则不涉及对于流域的离散，可以有效化解以上面元法中存在的问题，因而近年来受到许多学者的关注。目前，常用的无网格法有十多种，它们基本特征是将连续体离散为有限数量的质点集合，提供相应的近似函数，从而避免了繁琐的单元网格划分[2]。MFS法就是其中一种较新发展出的无网格的数值方法，该方法对于存在基本解的边值问题特别有效，并且物体几何形状越是复杂就越能体现出MFS法的优越性[3]。MFS法用流域控制方程基本解的线性组合作为流场的近似解，可以得到任意阶连续的导数，并且通过引入虚边界的概念完全避免了原先边界积分中存在奇点的问题。另外，研究指出MFS法具有收敛速度快和精度高的优点[4-5]；对于存在自由面或者移动边界的问题，MFS更能发挥自身的特点[6]，已被成功应用于三维造波模拟[7]以及斜向行进波遭遇障碍物后的演变模拟[8]等研究中，取得了很好的效果。

本次研究中进一步将MFS法引入船舶耐波性领域：利用MFS法计算有限水深二维剖面的水动力系数，并以此为基础，结合频域切片法理论预报了船舶在浅水中的耐波特性。以一艘Wigley船为例，证明了所提出算法的正确性和实用性。本文首先详细论述了MFS法的原理和计算方法；其次给出了MFS法求解有限水深二维剖面水动力系数的具体流程；接着简要回顾了切片理论的相关计算公式；然后给出了Wigley船在不同水深和航速下的垂荡和纵摇响应计算结果，并对结果进行了验证和分析；最后总结了本文的研究并对之后的研究工作进行了展望。

1 MFS法基本原理

势流问题由Laplace方程控制：

其中：Φ为流场的速度势。MFS法的核心思想是用基本解的线性组合拟合流场中的物理量，再让边界上的物理量满足给定的边界条件从而求出拟合物理量时未知的形状系数。因此，将速度势表达为如下形式：

其中：Pi为属于流域Ω的任意场点；c=［c1,c2,…,cN］T为拟合速度势的未知形状系数向量；S为包含源点Sj坐标的N维向量。

KD为Laplace方程的基本解，对于二维和三维问题分别有：

用MFS法进行计算时，首先要分别布置好场点和源点。场点为配置点，位于实际的流域边界上，需要满足对应的边界条件；源点则位于真实流场外的虚边界上（如图1所示），这样可以避免场点和源点重合时产生的奇点问题。需要指出的是，虚边界的选取（即源点的布置）对于MFS法的精度至关重要。若虚边界十分靠近真实边界，则形状系数求解矩阵的对角线元素值将趋近于无穷大，影响求解精度；而当虚边界远离真实边界时又将导致形状系数求解矩阵的条件数快速增长，使矩阵变得病态[9]。文献[10]中就源点的最优布置方法进行了探讨并指出虚边界的选取问题目前仍是制约MFS法发展的关键因素。本次研究通过数值试验进行不断尝试后发现：可以取物面场点间的平均间距作为虚边界位移量，由此根据每个场点的位置沿真实边界的外法向进行平移得到源点的布置位置。完成场点和源点的布置后，只要根据（2）式表达速度势并让每个场点处的速度势均满足流域边界条件即可。一般的边界条件分为Dirichlet型和Neumann型两种，因此有：

其中：fD和fN为Dirichlet和Neumann边界条件的一般表达；χD和χN为两种边界条件的组合系数。最后，对每个场点建立方程，得到如下形式的方程组：

求解后得到形状系数向量c，再由（2）式可求得流场内任意点的速度势及其任意阶导数。

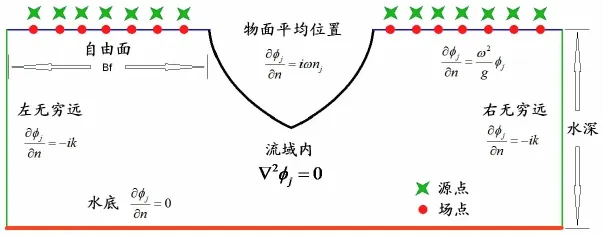
图1 MFS法求解二维剖面水动力系数Fig.1 Solving 2D section hydrodynamic coefficients based on MFS

2 有限水深二维剖面水动力系数计算

二维剖面水动力的求解包括横荡、垂荡和横摇三个模态，分别用下标2，3，4表示。有限水深情况下，计算各个模态速度势的定解问题（如图1所示）为：

其中：φj为规范化速度势，j=2，3，4；nj为物面处单位外法向量的j模态分量；ω0为波浪圆频率；k为波数与ω0间满足色散关系：

其中：H为水深。对于无穷远边界，只能在距浮体有限远处进行截断，并用两根垂线代替。这一处理无穷远边界的方法在采用简单格林函数的面元法中有过成功的应用[11-12]。

将（7）式至（10）式按（4）式的形式进行表达，并对每个场点建立相应的方程后进行求解，得到形状系数向量后可由（2）式得到物面上规范速度势的数值。由此可按（12）式计算出二维剖面的附加质量和阻尼系数：

3 频域切片理论

本文将二维剖面水动力计算与Salvesen等[13]提出的频域切片理论相结合，用于船舶垂荡和纵摇响应的预报。根据文献[13]建立坐标系，得到船体垂荡和纵摇的运动方程为：

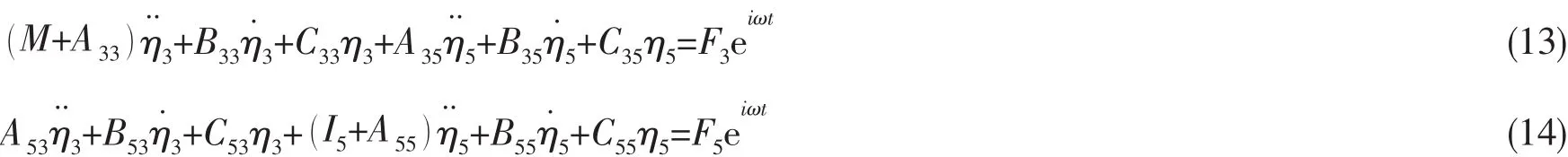
其中：η3和η5分别为垂荡和纵摇；M为船舶排水量；I5为船体纵摇惯量；ω为遭遇频率，与航速U和浪向β间满足关系：

Aij，Bij，Cij，F3和F5分别为对各个二维船体剖面积分后全船的附加质量、阻尼系数、恢复系数，一阶垂荡波浪力和一阶纵摇波浪力矩。详细的计算公式可参考文献[13]。

4 Wigley船计算结果

通过对一艘Wigley船的垂荡和纵摇响应计算结果验证MFS法结合切片理论预报船舶耐波性的有效性和实用性。Wigley船为数值船型，主要参数如表1所列。计算时先将船体沿垂线间长等间距分解为21个剖面，分别应用MFS法求解附加质量和阻尼系数，最后再通过切片理论积分得到全船的水动力系数并根据（13）式和（14）式求解运动响应幅值算子（RAO）。

表1 Wigley船主要参数Tab.1 Main particulars of Wigley Hull

首先计算了傅汝德数Fn为0.3的情况，并与Delft水池试验结果[14]和法国船级社三维频域面元法软件HydroSTAR的计算结果进行了对比。计算中，取水深为5倍的吃水；自由面宽度为6倍的船宽；物面上按0.02 m等间距布置场点，同时以0.02 m作为虚边界位移量布置源点。单侧自由面、水底和左/右无穷远边界分别布置60、60和50个场点。计算得到的垂荡和纵摇RAO如图2和3所示。

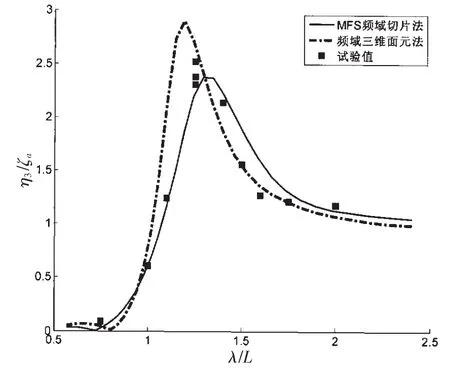
图2 垂荡响应计算结果验证Fig.2 Validation of heave response

图3 纵摇响应计算结果验证Fig.3 Validation of pitch response

从图中的对比可以发现，本方法的计算结果与试验符合较好，与频域面元法间存在一定差异，原因可能是由于频域面元法考虑了船体的三维特性并且在处理航速时与切片法有所不同造成的。

图4 水深对于垂荡响应的影响Fig.4 Effect of water depth on heave response

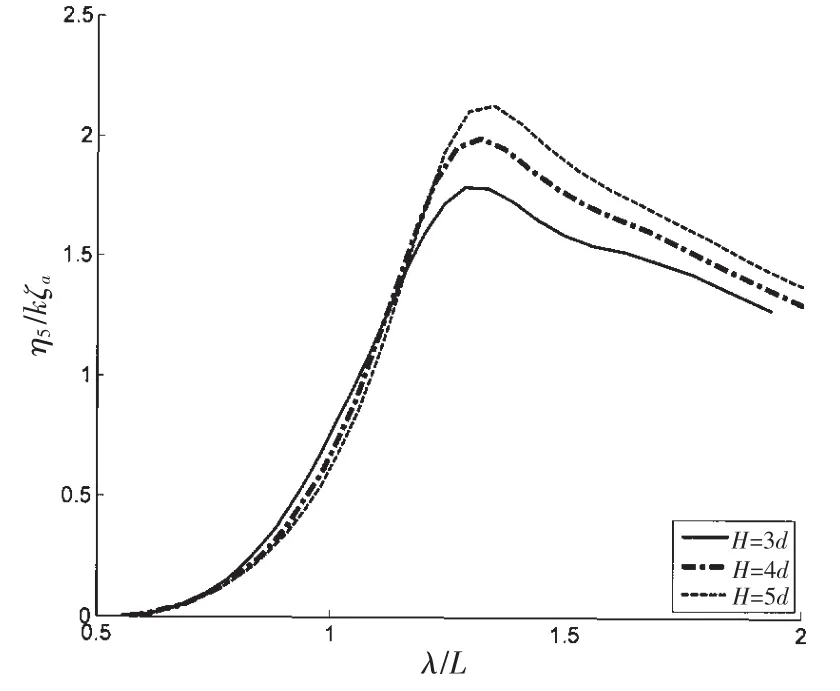
图5 水深对于纵摇响应的影响Fig.5 Effect of water depth on pitch response

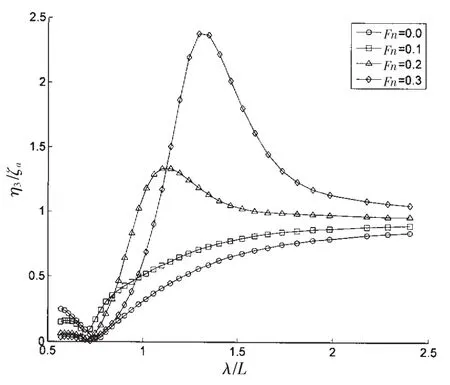
图6 航速对于垂荡响应的影响Fig.6 Effect of forward speed on heave response

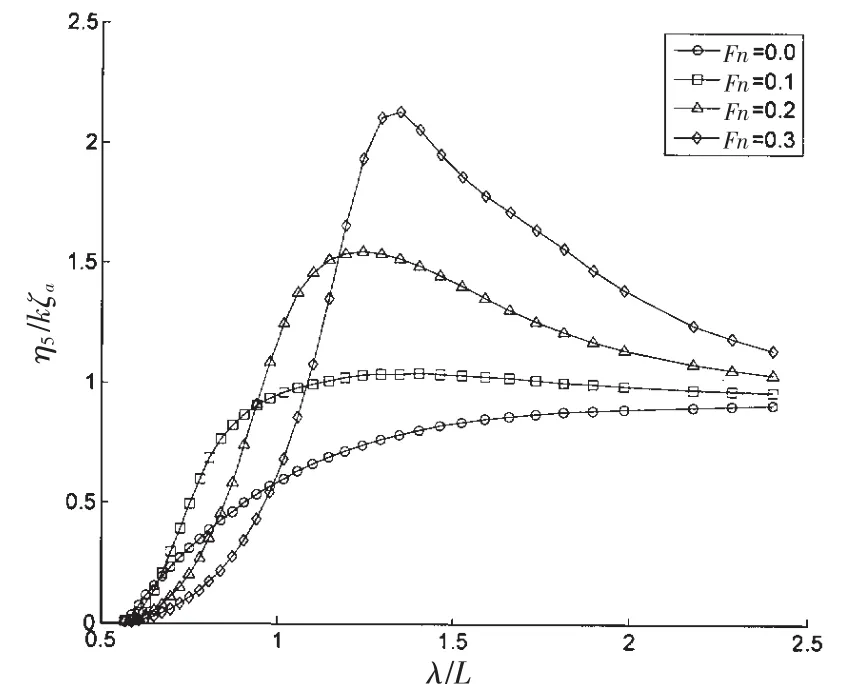
图7 航速对于纵摇响应的影响Fig.7 Effect of forward speed on pitch response

利用这套算法进一步研究了水深与航速对于该Wigley船耐波性的影响。先是计算了水深为3d，4d和5d水深下的垂荡和纵摇RAO曲线，d为船舶吃水。计算中根据水深的变化等量调整了左/右无穷远边界上的场点个数，分别为30，40和50，其他计算参数不变。从图4和5所示的结果中可以看出，水深对于垂荡和纵摇的峰值和长波区域的响应有一定影响，随着水深的增加响应变得更剧烈，三维面元法的计算结果也证实了这一变化规律。航速对于Wigley船垂荡和纵摇的影响如图6和7所示，分别计算了Fn=0.0，0.1，0.2和0.3四种情况下的RAO曲线。从图中可见，航速对于该船的影响十分显著，垂荡和纵摇的峰值随着航速的上升而显著增加。

5 结语

本文采用了一种新的无网格方法MFS研究了有限水深中二维剖面的水动力系数求解问题；提出了一套实用的数值方法，在求解过程中体现出了MFS法无奇性、不依赖网格、不涉及数值积分、数学原理简单和算法易于编程实现的优势。另外，将二维剖面水动力系数求解与频域切片法相结合，用于船舶耐波性的预报。以一艘Wigley船型为例，验证了方法的正确性和可行性，并借助该工具研究了水深和航速对于Wigley船耐波性的影响，结果表明这两个参数对于船舶耐波性有着很大的影响。本文研究为更深入地研究MFS法打下了基础，之后拟开展的工作包括虚边界的最优确定方法，MFS法在三维水动力计算中的应用以及MFS法在时域耐波性研究中的应用。这些研究将更能体现MFS法自身的优势，具有很好的应用前景。

[1]Hess J L,Smith A M O.Calculation of nonlifting potential flow about arbitrary three-dimensional bodies[J].J Ship Res, 1964,8(3)：22-44.

[2]王宇新,孙明,张建臣.无网格MPM法三维前处理系统设计[J].计算力学学报,2008,3：392-396. Wang Yuxin,Sun Ming,Zhang Jianchen.Implementation of 3D preprocessing program for material point method[J].Chinese Journal of Computational Mechanics,2008,3：392-396.

[3]Fairwather G,Karageorghis A.The method of fundamental solutions for elliptic boundary value problems[J].Advances in Computational Mathematics,1998,9：69-95.

[4]Peter M,Youssef F R.Convergence and stability of the method of meshless fundamental solutions using an array of randomly distributed sources[J].Eng Anal Bound Elem,2004,28：143-153.

[5]Li X.On convergence of the method of fundamental solutions for solving the Dirichlet problems of Poisson’s equation[J]. Advances in Computational Mathematics,2005,23：265-277.

[6]Sarler B.Solution of potential flow problems by the modified method of fundamental solutions：formulations with the single layer and the double layer fundamental solutions[J].Eng Anal Bound Elem,2009,33(12)：1374-82.

[7]Wu N J,Tsay T K.Applicability of the method of fundamental solutions to 3-D wave-body interaction with fully nonlinear free surface[J].J Eng Math,2009,63：61-78.

[8]Chen K H,Lu M C,Hsu H M.Regularized meshless method analysis of the problem of obliquely incident water wave[J]. Eng Anal Bound Elem,2011,35：355-362.

[9]Wang H,Qin Q H.Some problems with the method of fundamental solution using radial basis functions[J].Acta Mechanica Solida Sinica,2007,20(1)：21-29.

[10]Karageorghis A.A practical algorithm for determining the optimal pseudo-boundary in the method of fundamental solutions [J].Adv.Appl.Math.Mech.,2009,1(4)：510-528.

[11]Hasanadil M,Duan W Y,Wang Y.Hydrodynamic coefficients of ships with forward speed[J].Journal of Ship Mechanics, 2004,8(3)：46-54

[12]Milgram J H.Strip theory for underwater vehicles in water of finite depth[J].J Eng Math,2007,58：31-50.

[13]Salvesen N,Tuck E O,Faltinsen O M.Ship motions and sea loads[J].Trans.SNAME,1970,78：250-287.

[14]Journée J.Experiments and calculations on 4 Wigley hull forms in head waves[R].Report of Delft University of Technology,Ship Hydromechanics Laboratory,The Netherlands,1992.

Ship seakeeping prediction based on MFS meshfree scheme

FENG Pei-yuan1,MA Ning2,GU Xie-chong2
(1.Marine Design&Research Institute of China,Shanghai 200011,China;2.School of Naval Architecture, Ocean and Civil Engineering,Shanghai Jiaotong University,Shanghai 200240,China)

This paper presents a novel meshfree numerical scheme based on MFS(Method of Fundamental Solutions)for solving ship potential flow problems.This method adopts the fundamental solution of the potential flow control equation to represent the velocity potentials and can obtain any degree of continous velocity potential derivative.Moreover,through the introduction of pseudo boundary,the singularity in conventional Boundary Element Method(BEM)is circumvented.Compared with BEM,MFS has the merits of being desingularized,meshfree,integration-free,mathematically simple and easy for programming.This study explores the application of MFS in computing the hydrodynamic coefficients of two dimensional section in water of finite depth and proposes a practical numerical scheme;furthermore,MFS is combined with frequency domain strip theory to predict the heave and pitch response of a Wigley hull.The validity of the proposed numerical scheme is proved through comparison with panel method and experimental result.Finally,the influence of water depth and forward speed on seakeeping is studied using the current scheme.This study innovatively applies MFS into the filed of ship hydrodynamics and can provide some guidance for the future development of MFS.

MFS;meshfree;strip theory;potential flow;seakeeping

U661.1

A

10.3969/j.issn.1007-7294.2017.04.002

1007-7294（2017）04-0390-06

2016-10-07

国家自然科学基金（51579144）；工信部高技术船舶科研项目（K24352）

封培元（1987-），男，博士，E-mail：pyfeng23@163.com；马宁（1961-），男，教授，长江学者。