二维物体入水砰击问题的理论方法研究

寇莹，王宝寿，陈玮琪

（中国船舶科学研究中心，江苏无锡214082）

二维物体入水砰击问题的理论方法研究

寇莹，王宝寿，陈玮琪

（中国船舶科学研究中心，江苏无锡214082）

入水问题的研究在水动力学和海洋工程等领域有着重要的现实意义。文章采用Wagner模型的思想，将其中的相当平板理论改为椭圆拟合，得到了不同斜升角的二维楔形体匀速入水时的湿表面无量纲压力分布和砰击力，并与其它理论方法和数值计算结果相比较。椭圆拟合方法得到的压力分布在楔形体斜升角较小时与数值计算结果吻合良好，砰击力与数值计算结果在较大斜升角的情况下仍然很接近，比其它理论方法的适用范围更广，可以作为工程上估算砰击力大小的一种新方法。

入水砰击；Wagner方法；椭圆拟合

0 引言

入水现象在自然界中普遍存在，也是工程实际中经常遇到的问题，例如船舶航行时船艏与水面的拍击、返回舱水面着落、水上飞机的降落以及鱼雷入水等。砰击产生的水动力载荷会对结构物造成不利影响，引起结构物的变形和破坏，甚至导致严重的事故。因此，在工程设计中需要对入水砰击问题重点关注，许多学者也对该问题进行了分析和研究。最早关于入水砰击问题的研究是1929年von Karman[1]针对水上飞机降落问题的求解，将实际工程问题简化为二维物体入水模型，并将物体入水的附加质量用无限频率下同等宽度的平板在无界流场中的附加质量代替，利用动量守恒定律求得砰击力。由于该方法不考虑砰击时水面的变化，因此得到的砰击力不够准确。Wagner[2]发展了入水砰击理论，在势流理论框架下采用相当平板理论，并计入自由面升高，得到入水物体湿表面的压力分布和总砰击力。该理论的重点在于考虑了入水过程中的液面升高，对物体与流域的接触范围给出了修正，并且在二维轴对称情况下与实验数据能够较好地吻合，为后续的许多理论模型奠定了基础。

由于Wagner理论将实际入水问题做了许多简化，因此存在一定的局限性，比如只适用于入水初期阶段，而且物体入水深度与水平宽度相比为小量的情况。一些学者对该理论的不足进行了改进，Armand和Cointe[3]利用匹配渐近方法在接触区域边缘附近进行了修正；Logvinovich[4]通过在速度势分布的表达式中增加附加项使得接触区域边界的流速有界，可以较好地预报小斜升角楔形体入水的压力分布和砰击力结果；Korobkin[5]对Logvinovich方法作了进一步改进，在计算压力分布时保留了与斜升角有关的二阶项，得到MLM（Modified Logvinovich Model）方法，可以适用于斜升角更大的楔形体。Zhao等人[6]采用半解析模型，仅简化自由面的边界条件，液面隆起高度依然采用Wagner方法，结合边界元方法求解边值问题，考虑了伯努利方程的非线性，得到自由面的形状以及压力分布情况。Scolan和Korobkin[7]将Wagner理论拓展到三维入水问题中，对轴对称钝体Wagner问题进行渐近分析得到解析解。将Wagner理论与先进的数值计算方法相结合可以求解更复杂的流场方程和边界条件。

本文借用Wagner模型中以平板代替实际入水物体的思想，以垂直匀速入水的二维楔形体为研究对象，将楔形体用椭圆代替，浸湿表面的速度势近似为椭圆绕流的速度势分布，进而求得压力分布和砰击力，并将对不同斜升角的楔形体的计算结果与其他方法比较，验证椭圆拟合方法的可靠性。

1 入水理论基础

物体入水是一个复杂的现象，分析该问题需要进行合理的简化，虽然不可能得到浸入过程中流体流动的所有细节，但是理论模型降低了计算的难度并且保证了结果具有一定的精确度。由于结构物入水瞬间会产生很大的砰击力，该过程持续时间较短，剪切流动对流场的作用很小，边界层厚度与结构物的尺度相比为小量，因此流体的粘性作用可以忽略不计，该问题可以在势流理论框架下进行研究。基于势流理论的数学模型与实际问题相比得到了很大的简化，也便于解析解和数值计算结果的求取。

假设流体无粘性、不可压缩，并且流动无旋，则流场中速度势φ满足Laplace方程

根据动量守恒定律可以得到伯努利方程

其中：p为压力；ρ为流体密度；g为重力加速度；pa为环境大气压力，对流场的求解没有影响。由于结构物的运动速度较大而砰击时间很短，砰击力产生的加速度远大于g，因此伯努利方程中的重力作用项可以忽略。假设自由面上的压力恒为大气压，则可以忽略pa， 得到自由面动力学边界条件

自由面运动学条件为

在物面上满足条件：

2 Wagner模型及其改进方法

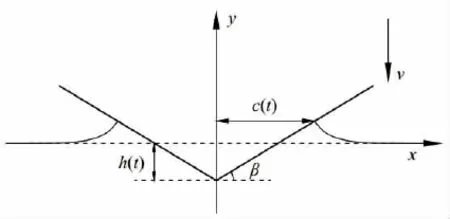
图1 二维楔形体入水示意图Fig.1 Sketch of two-dimensional wedge entering water

Wagner模型假设物体入水深度与水平宽度相比为小量，采用了von Karman模型的相当平板假设，并在此基础上考虑了自由面升高的影响，平板半宽为c（）t，如图1所示。以平板速度势代替物体浸湿部分的速度势分布，如下式所示：

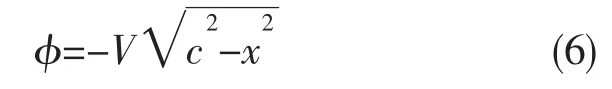
将速度势φ代入上式即可得到物面上的压力分布

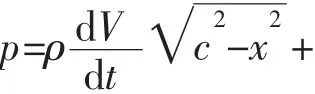
在浸湿宽度内对压力进行积分可得楔形体所受的砰击力

对于匀速入水情况，第二项为零。入水半宽c（）t可以根据Wagner条件求得：

其中函数f（x）表示对于斜升角为β的楔形体，f（x）=xtan β，所以

Wagner采用平板绕流速度势代替楔形入水，在楔形体湿表面x=±c处速度趋于无穷大，压力也趋于无穷大，这显然不符合实际情况，因此根据Wagner模型得到的砰击力偏大，仅适用于较小斜升角（≤30°）的楔形体入水砰击力估算。对于Wagner模型的改进方法中，比较典型的是在速度势分布的表达式中添加泰勒展开得到的高阶项，并且考虑伯努利方程中非线性项的影响，使接触区域边缘附近的流速有界，例如OLM（Original Logvinovich Model），MLM（Modified Logvinovich Model）方法。MLM方法[5]将原始Wagner模型速度势表达式在物面处进行泰勒展开，增加了其一阶项，得到新的速度势分布，这样使得MLM方法适用于更大斜升角的楔形体入水砰击力的求解。

若认为β为小量，忽略上式中关于β的二阶项，则得到OLM方法求解压力的表达式[5]：

两种方法求得的压力在接触区域边界的值趋于负无穷，在计算砰击力时只考虑压力为正的部分

其中：D（t）表示压力为正的区域，对于Wagner模型即为-c（t）＜x＜c（t），对于OLM和MLM方法则要计算p=0时的x值，得到D（t）的范围。OLM方法在斜升角较大时压力为正的区域与真实接触区域相比较小，积分得到的砰击力不够准确，因此适用的斜升角的范围相对较小，一般小于35°；理论上MLM方法在β＜arctan（π）≈72°范围内可以给出砰击力的合理预报。

3 椭圆拟合方法

椭圆拟合方法与平板拟合类似，将入水物体用椭圆来代替，用椭圆绕流的速度势分布表示物体浸湿表面的速度势，进而得到湿表面的压力分布和结构物所受的砰击力。与Wagner模型相比，椭圆拟合方法在物体表面与液面交界处流速有界，压力为有限值。图2为椭圆拟合示意图。

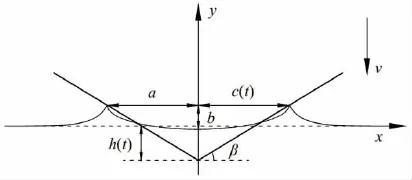
图2 椭圆拟合示意图Fig.2 Sketch of ellipse fitting

椭圆形状与物体形状有关，对于楔形体则与其斜升角相关。椭圆形状的确定沿用Wagner模型的思想，半长轴a等于入水半宽，即由公式（11）得到的c（）t。半短轴的长度b由半长轴a和斜升角β确定，β越大，物体与液面交界（即x=±a）附近流速越小，b与a的比值应当越大。为了使理论模型交界处附近压力尽量符合实际情况，b与a的关系式如下：

椭圆绕流复势[8]为

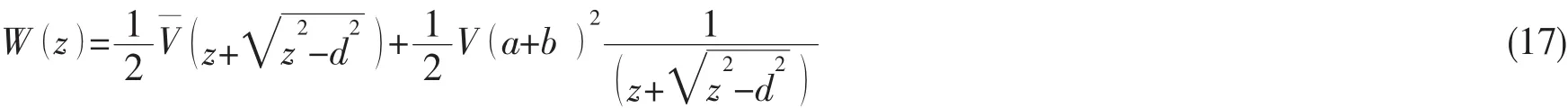
复势对时间t的偏导数为

椭圆拟合中长轴随时间的增加与Wagner模型入水半宽的增加相同，可以模拟楔形体入水时浸湿区域不断增大的情况，而公式（20）压力求解中包含了短轴增加的速度，相当于增加了物体的入水速度，导致压力偏大。根据公式（8）可知，Wagner方法得到的浸湿区域中心无量纲压力为k2，与P0′相差即短轴变化带来的压力。因此，为了压力求解更接近实际楔形入水的情况，应该去除短轴增加速度的影响，修正后的压力分布公式如下：

对上式进行积分可得到砰击力的无量纲值，即

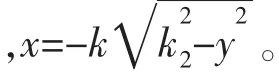
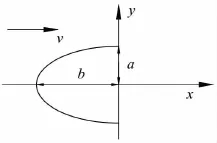
图3 b＞a时椭圆拟合示意图Fig.3 Sketch of ellipse fitting when b＞a

复势可表示为

对时间t的偏导数为

进一步求得的无量纲压力分布结果与公式（20）相同，因此b＞a时依然可以通过公式（22）和（23）求得压力分布和砰击力。

4 计算结果分析

图4给出不同方法计算得到的六种不同斜升角的楔形体无量纲入水压力分布曲线。

其中（a）、（b）、（c）中的数值计算曲线采用的是许国冬[9]的全非线性数值解，（d）、（e）、（f）的数值计算曲线采用的是Zhao和Faltinsen[10]的数值计算结果。从图中可以看出，β较小（10°-30°）的情况下接触区域中心（x=0）处的压力最小，在接触边缘附近达到最大值，β较大（40°-60°）的情况下接触区域中心处的压力最大。在β=10°时几种方法得到的压力分布曲线都十分接近，随着β的增加，Wagner方法的结果与其他方法的差别逐渐增加，在β=30°时的压力已经明显大于其他方法，反映出该方法只适用于小斜升角的楔形体入水，在β＞30°的情况下并未将其计算结果画入图像中进行比较。

由于理论方法对实际问题做了较多的简化，与数值计算相比无法反映入水过程的非线性情况，压力分布的结果可靠度不高。椭圆拟合和MLM方法的压力分布结果与数值计算结果在β≥30°时已经有较大的偏差，特别是MLM方法在β≥40°时的曲线形状与数值计算明显不同，反映的压力分布规律相差较大，而椭圆拟合的压力分布的趋势更接近数值计算，与实际情况更接近。

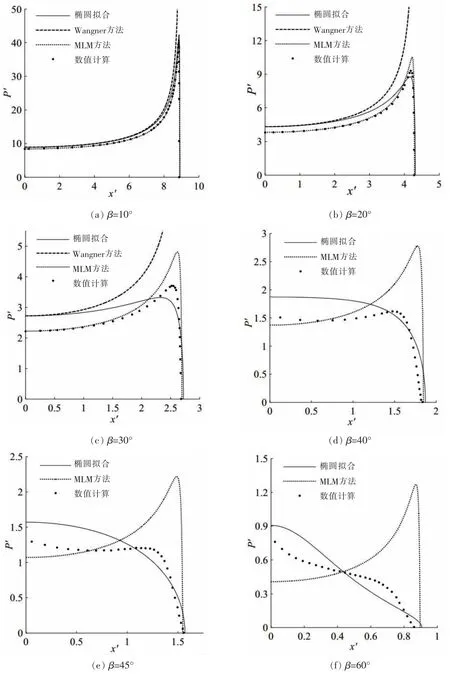
图4 不同斜升角的楔形体入水压力分布结果Fig.4 Non-dimensional pressure distribution of wedges of different deadrise angles entering water

表1为本文椭圆拟合方法、MLM方法、Zhao和Faltinsen[10]以及许国冬[9]数值计算得到的无量纲砰击力的比较。从压力分布图中可以看出Wagner方法计算所得结果偏大，相应的砰击力也比其他方法大，因此该方法的砰击力结果未列入表1。

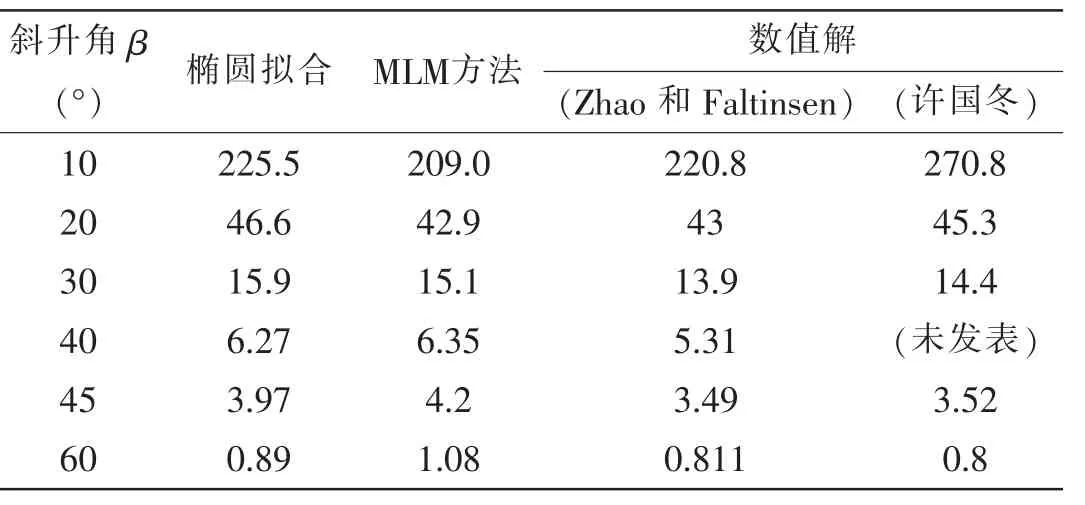
表1 入水砰击力结果Tab.1 Hydrodynamic force of water impact

从表1中可以看出，在楔形体斜升角为10°-60°范围内，椭圆拟合与数值计算的结果都比较接近；β较小（10°-30°）时砰击力比MLM方法稍大，在β较大（40°-60°）时与MLM方法的结果相比更接近数值计算结果。结合图4中β在40°-60°时的两种方法的压力分布情况，椭圆拟合的压力分布和砰击力都比MLM方法更准确。以工程应用的角度来看，椭圆拟合方法适用于斜升角在较大范围内的楔形体入水砰击力的估算，结果比数值计算稍大，与MLM方法相比更有优势。

5 结论

Wagner方法奠定了入水砰击问题的理论基础，本文参考该方法中的相当平板理论，将入水物体用椭圆代替，椭圆形状根据Wagner方法求得的物体入水宽度确定。椭圆拟合使得物体与液面接触边缘附近的流速为有限值，改善了Wagner方法的缺陷，而且不会出现其他Wagner改进方法（OLM，MLM）中接触区域边缘压力趋于负无穷的情况。本文计算了斜升角为10°-60°的二维楔形体匀速入水的压力分布和总砰击力，并与其他理论方法和数值计算结果对比。比较结果表明，斜升角较小时，理论方法的压力分布与数值计算结果相差较小，斜升角逐渐增加时差距也逐渐明显，但是在大斜升角情况下椭圆拟合的结果比MLM方法更接近数值结果；从砰击力结果上看，椭圆拟合与数值计算结果吻合良好，在斜升角较大的情况下比MLM方法更为准确，适用范围受斜升角限制更小，比数值计算方法更为简便，可以作为工程上估算物体入水砰击力的一种方法。

[1]Von Karman.The impact on seaplane floats during landing[R].Technical Notes.No.321.National Advisory Committee for Aeronautics,1929.

[2]Wagner H.Uber stoss-und gleitvorgange an der gberflache von glussigkeiten[J].Z.angew.Math.Mech.,1932,12(4)：193-215.

[3]Armand J L,Cointe R.Hydrodynamic impact analysis of a cylinder[C].Proc.Fifth Int.Offshore Mech.and Arctic Engng. Symp.,1987：609-634.

[4]Logvinovich G V.Hydrodynamics of flows with free boundaries[M].New York：Halsted Press,1973.

[5]Korobkin A A.Analytical models of water impact[J].Euro.Jnl of Applied Mathematics,2004,15：821-838.

[6]Zhao R,Faltinsen O M,Aarsnes J.Water entry of arbitrary two-dimensional sections with and without separation[C].Proc. 21st Symposium on Naval Hydrodynamics,1996：118-133.

[7]Scolan Y M,Korobkin A A.Three-dimensional theory of water impact.Part 1.Inverse Wagner problem[J].J Fluid Mech., 2001：293-326.

[8]吴望一.流体力学[M].北京：北京大学出版社,2013.

[9]许国冬.流体/刚体砰击问题及相似解研究[D].哈尔滨：哈尔滨工程大学,2008. Xu Guodong.A study of fluid/rigid body impact problem and its similarity solution[D].Harbin：Harbin Engineering University,2008.

[10]Zhao R,Faltinsen O M.Water entry of two-dimensional bodies[J].J Fluid Mech.,1993,246：593-612.

Astudy of theoretical method for two-dimensional water impact problems

KOU Ying,WANG Bao-shou,CHEN Wei-qi
(China Ship Scientific Research Center,Wuxi 214082,China)

Water impact problems have practical importance in several fields such as ship hydrodynamics and ocean engineering and received considerable attention.Wagner created the basis of the applied theory of water impact and his concepts and ideas are still in use.This paper refers to the idea of Wagner model which substitutes the entering body with a flat plate.Instead,the flat plate fitting is replaced by ellipse fitting.This method is used to analyze the hydrodynamic force and pressure distribution of two-dimensional wedges of different deadrise angles.The results are compared to those obtained by other theoretical and numerical methods.Pressure distribution shows good agreement with numerical results when the deadrise angle is small.The hydrodynamic force is also closed to numerical results and more accurate even when the deadrise angle is large.This method can apply to entering bodies of a large range of deadrise angles and has a good value in engineering application of estimating hydrodynamic forces during water impact.

water impact;Wagner model;ellipse fitting

O352

A

10.3969/j.issn.1007-7294.2017.04.001

1007-7294（2017）04-0383-07

2016-09-22

寇莹（1994-），女，硕士研究生；王宝寿（1963-），男，研究员。