基于AR功率谱和ZAM变换的FSK-BPSK复合信号参数估计*

刘 歌，张旭洲，汪洪艳

(空军航空大学 信息对抗系，长春 130022)

基于AR功率谱和ZAM变换的FSK-BPSK复合信号参数估计*

刘 歌*，张旭洲，汪洪艳

(空军航空大学 信息对抗系，长春 130022)

为了解决频率编码-二相编码(FSK-BPSK)复合调制信号参数估计精度低的问题，提出利用自回归(AR)模型功率谱估计联合ZAM(Zhao,Atlas,and Marks)变换的方法。首先，利用AR模型功率谱估计方法对信号相位不敏感的特点，对FSK-BPSK复合调制信号的跳频分量数以及跳频码元序列进行估计；然后，利用ZAM分布对相位变化极其敏感的特点，提取信号ZAM分布的各跳频频率下的截面，对相位编码的码元宽度和跳频码元宽度进行估计。仿真实验表明，在全频段信噪比不小于0 dB时，AR模型功率谱联合ZAM变换的方法能够精确地估计出该复合信号的各参数。

复合调制信号；参数估计；自回归模型功率谱；ZAM变换

1 引 言

现代雷达系统中复合调制信号的应用日益广泛，其中频率编码-相位编码(Frequency Shift Keying- Binary Phase Shift Keying,FSK-BPSK)复合调制信号因具有大时宽带宽积、高分辨率和低截获概率的优点而成为另一个典型的复合调制雷达信号。这种信号将频率编码和相位编码的技术相结合，并且集中了两种调制方式的优点，克服了单一调制方式的不足。由于FSK-BPSK复合调制信号的时宽带宽积比频率编码或相位编码信号的大，因此降低了截获概率，是一种很好的低截获概率雷达信号[1]。但是多种调制方式的混合必然会造成信号自身的复杂，所以其参数估计成为了一大难题。即使频率编码、相位编码两种单独的调制方式的参数估计技术已经较为成熟，也不能直接作用于FSK-BPSK复合调制信号的参数估计问题上。因而，对FSK-BPSK复合调制信号的参数估计进行研究对现代电子侦察具有重要的现实意义。

对于FSK-BPSK复合调制信号的参数估计，已有相关的研究。文献[2]对FSK-BPSK复合调制信号进行了基本介绍；文献[3]对FSK-BPSK复合信号的功率谱密度进行简要地分析；文献[4]将四阶循环累积量算法、时频脊线分析与小波变换相结合对信号进行参数估计，但是直接对各参数进行估计，容易造成调制形式互相干扰，从而导致整个参数估计过程比较复杂；文献[5]提出利用Zhao,Atlas,and Marks(ZAM)变换与快速傅里叶变换对2FSK-BPSK信号进行参数估计；文献[6]利用Haar小波和正弦波频率估计的方法实现FSK-BPSK复合调制信号的参数估计，但是为了将两种调制方式分开，而对信号进行平方处理以消除相位调制先分析频率调制的方法会导致信噪比的降低，影响估计性能。

针对上述问题，本文提出利用自回归模型(Autoregressive model，AR)功率谱与ZAM分布相结合的参数估计方法。首先，计算信号的AR功率谱，估计FSK-BPSK信号的跳频分量数以及跳频码元序列；然后，对信号进行ZAM变换，提取信号ZAM分布的各跳频频率下的截面，估计出信号相位编码的码元宽度和跳频码元宽度。

2 信号模型

FSK-BPSK复合调制信号实质上是在频移键控的基础上进行二相编码(Binary Phase Shift Keying,BPSK)，其表达式为

(1)

式中：u0(t)表示单位函数，满足

Tf表示频率编码(FrequencyShiftKeying,FSK)的子脉冲宽度；Tp表示BPSK的子脉冲宽度；θi表示信号的调制相位，且θi=π·Ci；fk表示FSK序列中第k个跳频频率，满足

fk=(k+1)f0, k=0,1,…,K-1 。

(2)

式中：f0表示倍频分量，满足f0=1/Tp[4]；K表示跳频分量数。

FSK-PSK复合调制信号的表达式见式(1),其调制过程大致如下：将FSK信号的跳频序列记为{f0,f1,…,fK-1}，BPSK信号的编码序列记为{C0,C1,…,CNp-1}，信号的持续周期为T。

(1)将长度为T的脉冲信号等分为K个宽度为Tf的子脉冲；

(2)在各个子脉冲之间进行FSK；

(3)将FSK后的子脉冲再等分为Np个宽度为Tp的BPSK的码元，且满足Tf=NpTp；

(4)对各跳频脉冲进行BPSK，即可得到FSK-BPSK信号。

图1给出了4FSK-BPSK复合信号的时频特征图和频谱图。从时频特征图中可以明显地看出，该信号是在FSK的各跳频分量上进行相位编码，兼具了FSK和BPSK两种信号的特征。

图1 4FSK-PSK复合调制信号的时频特征图

3 参数估计原理

3.1 AR功率谱估计信号的跳频分量数、跳频序列

AR模型的谱估计是现代谱估计法中的一种方法，模型和信号自相关函数之间的关系是一组线性方程，运算简单，处理速度快，与建立在外推自相关函数时保持原概率空间的最大熵法是等价的，同时在作谱估计时，由于具有递推特性，所以所需的数据较短。因此,本文选择AR模型的功率谱估计方法对该多分量信号进行参数估计。

本文采用Burg递推法计算AR模型的参数，大量实验表明，该方法可以避免计算自相关函数，计算量比较小，且分辨率优于自相关法，性能优良。图2给出了4FSK-BPSK信号的频谱和功率谱对比，其中信噪比为5 dB。特别说明，文中采用的信噪比均为全频段信噪比，后文中不再说明。图2(a)显示的是4FSK-BPSK信号通过傅里叶变换得到的频谱图，图2(b)显示的是该信号经过AR功率谱计算得到的谱图。通过两幅图像的对比不难发现，快速傅里叶变换之后的频谱图的谱峰受噪声影响较大，模糊不清，难以提取,而AR功率谱得到的谱图，尖峰明显，受噪声影响较小，因此通过设置合适的门限，统计过门限的峰值个数可以估计出信号的跳频个数K，统计各峰值的位置所对应的横坐标可以估计出各跳频频率的值，从而得到跳频序列{f0,f1,…,fK-1}。

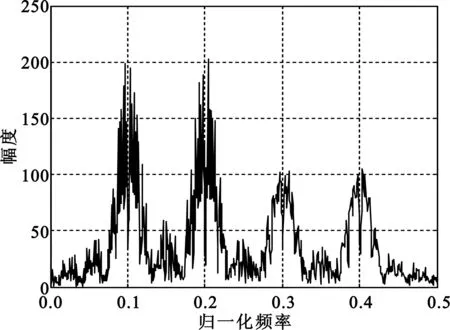
(a)频谱图

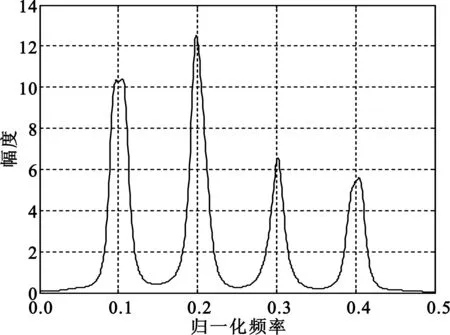
(b)AR功率谱图

3.2 ZAM变换估计相位编码码元宽度Tp及跳频码元宽度Tf

ZAM变换是一种基于核函数改进的时频分析方法，具有较好的时频聚集性，并能够抑制交叉项的干扰，最特别的一点是，这种时频分布对相位变化极为敏感，因此可以用来对相位编码信号进行参数估计。

信号s(t)的ZAM分布表达式为[8]

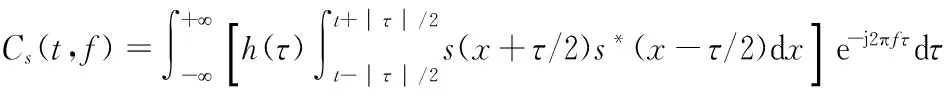
(6)

式中：*表示复数共轭，h(τ)表示窗函数。

文献[5]中己经证明了BPSK信号的ZAM分布会在载频截面对应的相位跳变点处产生一负峰值。由于篇幅有限，此处不再证明。

图3为信噪比为5 dB的条件下4FSK-BPSK信号的ZAM分布图，其中相位编码为5位Barker码，码宽为32。由图3(a)可知，在4FSK-BPSK复合调制信号的ZAM三维分布图中，BPSK的相位跳变点处会出现负峰值；图3(b)为某一跳频频率下的截面图，从图中曲线可以看出BPSK的码元宽度可以通过计算相邻负峰值之间的距离的最小值得到[9]；将不同跳频频率下的ZAM分布截面图合并到一个坐标系下，可以得到图3(c)中所示的曲线图。从图中可以看出，信号跳频频率的码元宽度可以通过相邻截面曲线第一个负峰值之间的距离较精确地估计出来。

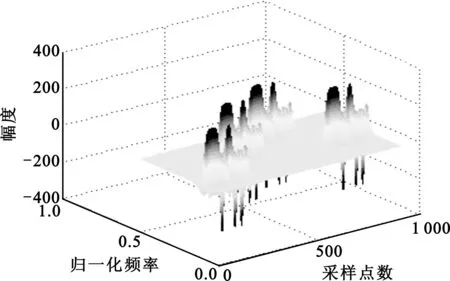
(a)ZAM三维分布

(b)某一跳频频率下的截面图

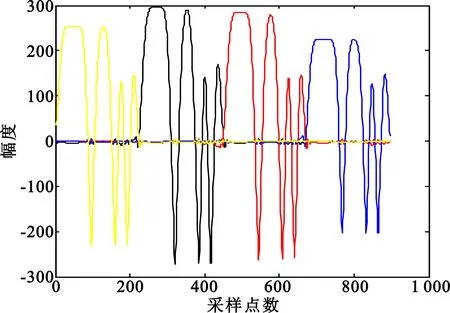
(c)所有跳频频率下的截面图

4 参数估计方法步骤

通过上述分析可知，由信号的AR功率谱可以提取FSK-BPSK复合调制信号在低信噪比下的跳频个数K和跳频序列{f0,f1,…,fK-1}，而通过对信号进行ZAM变换可以得到信号的跳频码元宽度Tf和相位编码码元宽度Tp，具体估计流程如下：

(1)跳频个数K和跳频序列{f0,f1,…,fK-1}

Step 1 采用Burg递推法计算信号的AR功率谱。

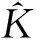
(2)跳频码元宽度Tf及相位编码码元宽度Tp估计

Step 1 根据公式，计算信号的ZAM分布，得到Cs(t,f)。

Step 3 在该截面上进行负峰值搜索，将负峰值出现的时间点记为

t={t1,t2,…,tm}，

(7)

并计算相邻负峰值之间的时间间隔

Δti=ti+1-ti,i=1,2,…,M-1。

(8)

找到Δti中的最小值Δtmin即为相位编码码元宽度的估计值为

(9)

找到Δti中的最小值Δtmin，利用Δti和Δtmin计算码元个数的估计值

(10)

因此，BPSK的码元宽度的估计值为

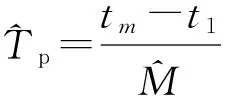
(11)

Step 4 记录每一截面曲线的第一个负峰值位置，并记为gi={g1,g2,…,gK}，其中i表示跳频分量数，且i=1,2,…,K。对gi进行一阶差分，得到的Δgi={Δg1,Δg2,…,ΔgK-1}，所以，信号的跳频码元宽度的估计值为

(12)

具体流程如图4所示。

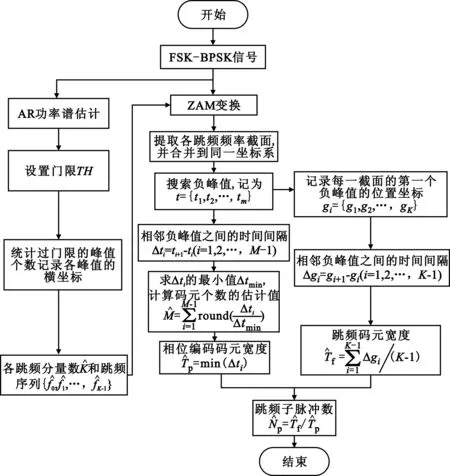
图4 FSK-PSK信号参数估计算法流程图

5 仿真实验及分析

为了验证本文方法的性能，对FSK-BPSK信号按照图4所示的参数估计算法流程图，在Matlab 2012a的环境下进行参数估计仿真实验。仿真条件：采样频率设置为500 MHz；跳频的4个频率分别设置为f1=160 MHz，f2=170 MHz，f3=180 MHz，f4=190 MHz；跳频脉冲宽度设置为Tf=2 μs，相位编码码元宽度设置为Tp=0.2 μs，且各跳频码元内的二相编码相互独立；噪声采用加性高斯白噪声，其均值为0，方差为1。仿真实验中的噪声均为全频段噪声。

实验一：在典型信噪比(SNR=0 dB)的条件下，对仿真信号做500次蒙特卡洛实验，并求这500次实验中的各参数估计值的平均值以及标准差，结果如表1所示。

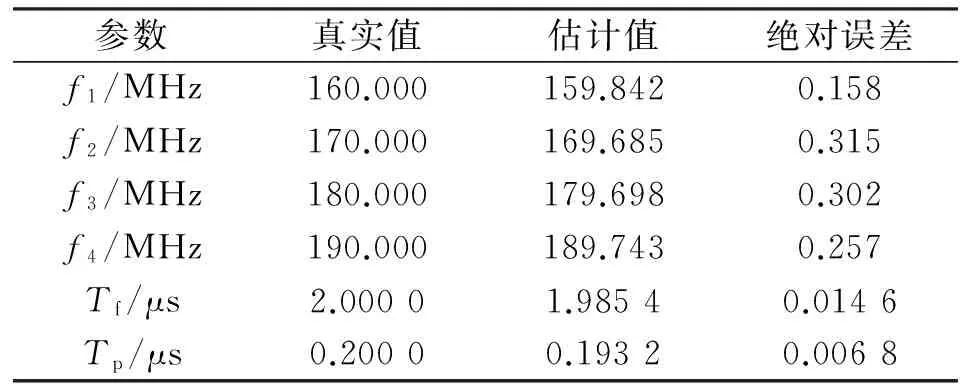
表1 信噪比为0 dB时信号各参数的估计精度

通过表1可以看出，在信噪比为0 dB的条件下，本文算法对FSK-BPSK信号各参数估计值与真实值之间相差不大。

实验二：为进一步验证本文算法的有效性，将本文算法与文献中常用的3种算法进行参数估计精度的对比，且以均方根误差(Normal Root Mean Square Error,NRMSE)随信噪比变化的曲线如图5所示，同时采为衡量标准。

在相同的仿真条件下，将本文算法与文献[4]中的四阶循环累积量算法、时频脊线分析与小波变换相结合的方法、文献[5]中的ZAM变换与快速傅里叶变换方法、文献[6]中的Haar小波和正弦波频率估计的方法进行对比实验，信噪比的取值范围为-10～5 dB，每隔1 dB做100次蒙特卡洛实验，并计算每一参数的RMSE，作出对比图如图5～7所示。

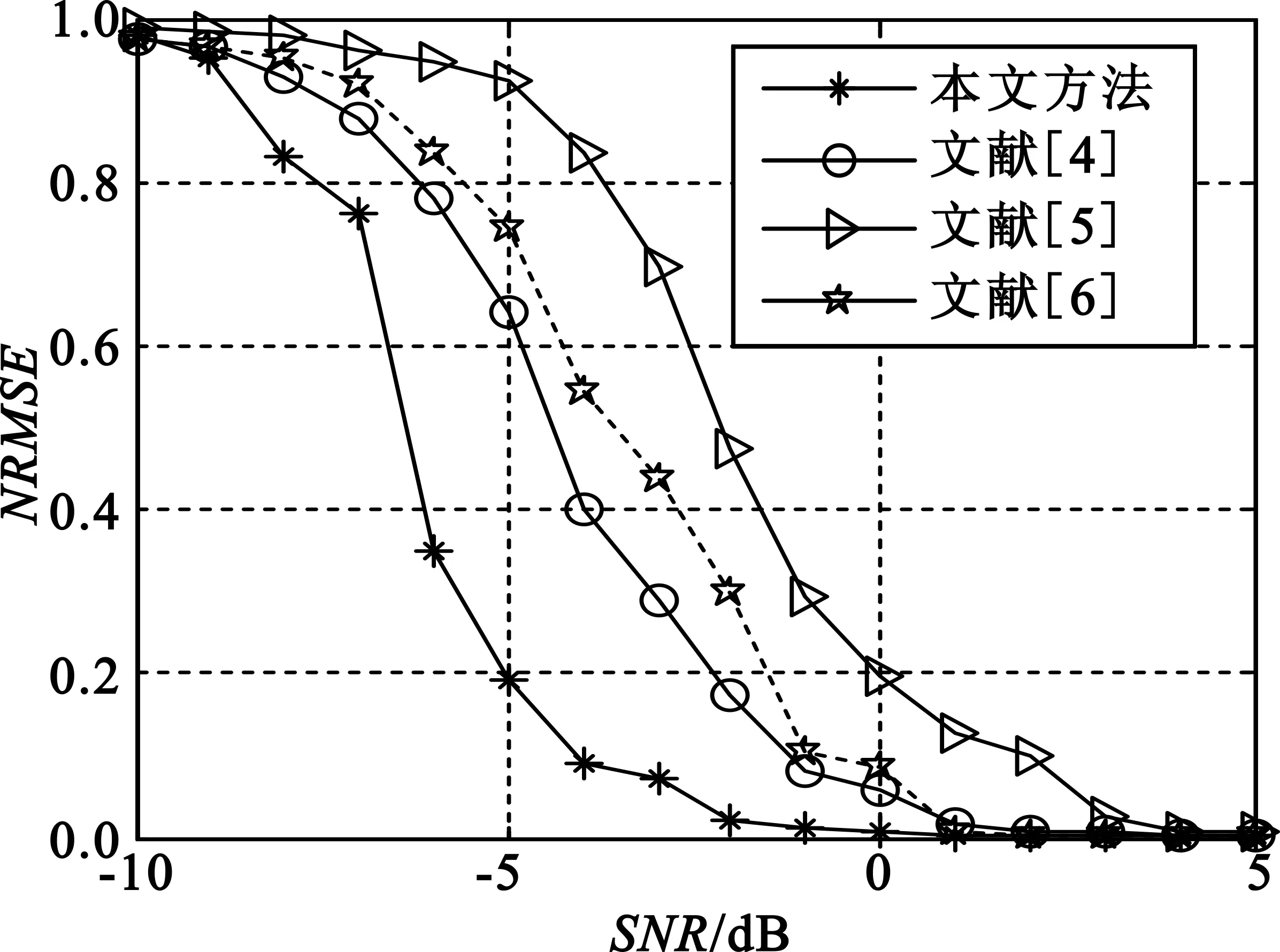
图5 跳频分量数误差曲线图

图6 倍频分量估计误差曲线图

图7 跳频脉冲宽度估计误差曲线图

通过3幅仿真图的总体趋势可以看出，在信噪比为-10～5 dB的范围内，本文对FSK-BPSK信号的参数估计算法具有较低的信噪比门限和较高的参数估计精度，即本文算法的性能要优于其他3种对比算法。从图5和图6中可以看出，本文算法在估计FSK-BPSK信号的跳频分量数和倍频分量时具有很高的精度，当信噪比大于等于0 dB时，均方误差小于0.05。这是因为AR功率谱对信号的相位变化不敏感，因此对信号进行功率谱分析时得到的峰值可以避免相位编码的干扰，且功率谱不易受到噪声干扰，在数据较短或不完全平稳时一样能够获得良好的估计精度[10]，因而具有良好的参数估计性能。从图7中的FSK-BPSK信号的跳频脉冲宽度的估计误差对比中可以看出，本文算法的性能与其他几种方法相差不大，但仍优于其他方法，这是因为信号的ZAM分布能够在相位跳变的位置得到精确的负峰值，通过提取相邻负峰值之间的距离对相位编码码元宽度进行估计，抗噪性较好。

6 结束语

本文针对FSK-BPSK复合调制信号参数估计精度较低的问题，详细地分析了该复合信号的特征，提出了联合AR功率谱和ZAM变换两种算法实现该信号高精度的参数估计。仿真实验表明当信噪比大于等于0 dB时，信号的各参数能够精确地估计。且在相同的全频段信噪比条件下，本文算法的参数估计精度明显高于对比文献算法。该方法原理较为简单，可以为该类型的复合调制信号的参数估计提供新的思路。

但是，本文算法中AR功率谱和ZAM分布的总体计算量较其他文献的算法没有明显的优势，后期研究工作将围绕降低算法计算复杂度展开，寻求提高估计精度与减小总体计算复杂度之间的平衡。

[1] 郭贵虎,文贻军,戴天. 一种新型低截获FSK/PSK雷达信号分析[J].电讯技术,2009,49(8):49-53. GUO Guihu,WEN Yijun,DAI Tian. Analysis of a new FSK/PSK radar signal with low probability of interception[J].Telecommunication Engineering,2009,49(8):49-53.(in Chinese)

[2] YANG H B,ZHOU J J,WANG F,et al. Design and analysis of Costas/PSK RF stealth signal waveform[C]//Proceedings of 2011 IEEE CIE International Conference on Radar.Chengdu:IEEE,2011:1247-1250.

[3] DENIZ C,IBRAHIM A,UMIT A. FSK/PSK modulated coded cooperation systems[C]//Proceedings of the 3rd International Conference on Communication Theory,Reliability,and Quality of Service.Athens:IEEE,2010:9-14.

[4] 雷雪梅,吕镜清,杨万麟,等. FSK/PSK混合调制信号多参数估计[J].电子信息对抗技术,2009,24(6):9-13. LEI Xuemei,LYU Jingqing,YANG Wanlin,et al. Multi-parameter estimation for hybrid modulated FSK/PSK signals[J].Electronic Information Warfare Technology,2009,24(6):9-13.(in Chinese)

[5] 曾小东,曾德国,唐斌. 基于ZAM-GTFR的2FSK/BPSK复合信号参数估计方法[J].电子信息对抗技术,2011,26(2):9-15. ZENG Xiaodong,ZENG Deguo,TANG Bin. Parameter estimation approach of 2FSK/ BPSK hybrid signal based on ZAM-GTFR[J].Electronic Information Warfare Technology,2011,26(2):9-15.(in Chinese)

[6] 宋军,刘渝,王旭东. FSK/BPSK复合调制信号识别与参数估计[J].电子与信息学报,2013,35(12):2870-2873. SONG Jun,LIU Yu,WANG Xudong.The recognition and parameter estimation of hybrid modulation signal combined with FSK and BPSK[J].Journal of Electronics & Information Technology,2013,35(12):2870-2873.(in Chinese)

[7] 闫庆华,程兆刚,段云龙. AR模型功率谱估计及Matlab实现[J].计算机与数字工程,2010,38(4):154-156.

YAN Qinghua,CHENG Zhaogang,DUAN Yunlong. Power spectrum density estimation for AR model and the simulation in Matlab[J].Computer & Digital Engineering,2010,38(4):154-156.(in Chinese)

[8] ZHAO Y,ATLA L E,MARK R J. The use of cone-shaped kernels for generalized time - frequency representations of nonstationary signals[J].IEEE Transactions on Acoustic,Speech,Signal Processing,1990,38(7):1084-1091.

[9] 王星,曹晋龙,赵玉,等. 基于瞬时测频的BPSK和QPSK信号参数估计[J].电讯技术，2014,54(4):430-436. WANG Xing,CAO Jinlong,ZHAO Yu,et al. Parameter estimation of BPSK and QPSK signals based on IFM[J].Telecommunication Engineering,2014,54(4):430-436.(in Chinese)

[10] 胡广书.数字信号处理—理论、算法与实现[M].北京:清华大学出版社,2003:527-574.

Parameter Estimation of FSK-BPSK Hybrid Modulation Signal Based on AR Power Spectrum and ZAM Transform

LIU Ge,ZHANG Xuzhou,WANG Hongyan

(Department of Information Countermeasures,Aviation University of Air Force,Changchun 130022,China)

In order to solve the low accuracy problem of parameter estimation of Frequency Shift Keying-Binary Phase Shift Keying(FSK-BPSK) hybrid modulation signals,a method combining autoregressive model(AR) power spectrum with Zhao,Atlas,and Marks(ZAM) distribution is proposed. First,by using the feature that the AR power spectrum is not sensitive to the phase of the signal,the component numbers of the hopping frequency and hopping frequency sequence of FSK-BPSK signal are estimated by AR power spectrum.Then,by using the feature that the ZAM distribution is extremely sensitive to the phase changing,the phase-coded code width and frequency hopping code width are extracted by the ZAM transform. Simulation results show that the parameters of the signal can be estimated precisely when the signal-to-noise ratio(SNR) is not less than 0 dB.

hybrid modulation signal；parameter estimation;autoregressive model(AR) power spectrum;ZAM transform

10.3969/j.issn.1001-893x.2017.04.011

刘歌，张旭洲,汪洪艳.基于AR功率谱和ZAM变换的FSK-BPSK复合信号参数估计[J].电讯技术，2017,57(4):430-435.[LIU Ge,ZHANG Xuzhou,WANG Hongyan.Parameter estimation of FSK-BPSK hybrid modulation signal based on AR power spectrum and ZAM transform[J].Telecommunication Engineering,2017,57(4):430-435.]

2016-07-04；

2016-10-17 Received date:2016-07-04；Revised date：2016-10-17

TN971.1

A

1001-893X(2017)04-0430-06

刘 歌(1991—)，女，山东威海人，2014年获军事情报学学士学位，现为硕士研究生，主要研究方向为复杂调制雷达信号的处理；

Email:yyliuge@sina.com

张旭洲(1982—)，男，陕西户县人，讲师，主要研究方向为雷达对抗侦察情报分析；

汪洪艳(1979—)，女，吉林长春人，硕士，讲师，主要研究方向为雷达信号处理。

*通信作者：yyliuge@sina.com Corresponding author：yyliuge@sina.com