一种新型液压管道抗振支承研究

熊宇，张怀亮,2，彭欢

(1.中南大学高性能复杂制造国家重点实验室，长沙410083；2.中南大学机电工程学院，长沙410083）

一种新型液压管道抗振支承研究

熊宇1，张怀亮1,2，彭欢1

(1.中南大学高性能复杂制造国家重点实验室，长沙410083；2.中南大学机电工程学院，长沙410083）

根据管道减振原理，设计一种新型管道液压抗振支承。该液压管道支承通过弹簧、弹簧片对振动能量进行吸收，并具有结构简单、安装方便的优点。建立振动环境下液压管道振动的数学模型，通过仿真分析安装抗振支承前后管道应力的波动响应，并进行实验验证。结果表明：该抗振支承能有效减小管道应力和流体波动，减振后管道应力最大值和流体压力平均波动幅值分别减小了14.80%、40.49%，有关结论能为在基础振动环境下的管道抗振提供一定的依据和参考。

振动与波；基础振动；液压管道；抗振支承；压力波动

许多工程机械工作环境恶劣，如矿山机械、硬岩掘进机（TBM）等[1]。在工作过程中，载荷突变势必会使设备产生强烈振动，导致安装在其上的输流管道振动加剧，大的横向振动位移会使管壁产生大的应力，这极易导致管道出现疲劳破坏，影响工作效率和人员安全。同时轴向振动会加剧管道振动，引起管内流体产生流速和压力的巨大波动，波动的流体会对下游液压系统造成大的冲击，影响流体和整个液压系统的稳定性和动态品质[2–3]。因此，对于强振动环境中的输流管道进行减振设计是亟待解决的问题。

国内外在管道减振方面的主要对策包括降低振源振动、增加隔振器隔开振源、调整结构阻尼衰减振动能量、增加管道结构刚度以避开共振、增加控制系统主动减弱管道振动等[4–6]。谢敬华对盾构机上的长管道进行液控系统动态响应研究，通过仿真分析管道结构参数对系统的影响规律[7]。曾胜利用调谐质量阻尼器进行管路系统减振[8]。Shin Y在振源和管道中间设置阻尼器，加快振动衰减[9]。Yau对自激振动管道的控制系统进行设计，通过电压控制压电式作动器的力矩，实现对管道的振动控制[10]。Kwong通过调整管道固有频率，使管道远离共振区域[11]。

上述研究对支承间距及材料等方面做了较深入的分析，但在管道抗振策略研究及对抗振支承的研究鲜见报道，且现有管道支承的设计都过多侧重于对横向振动进行减振，而忽视了轴向振动的影响。因此，设计一种适用于横向和轴向的新型液压管道抗振支承，对振动环境下液压管道减振设计具有一定的指导意义。

1 减振原理

对管道两端设置如图1轴向和横向的弹簧和阻尼，实现对轴向和横向振动的隔离。

图1 管道减振模型

忽略管道内部流体振动、管道弯曲变形和流固耦合的影响，将管道视作一个质量块，则所建模型简化为一个简单的振动系统。设x(t)和x1(t)分别为质量块及基础的位移，基础的运动规律为

由达朗伯原理得到如下的运动方程

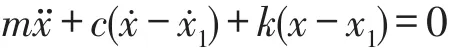
可化简为

将式（1）代入式（2），得到

设方程式（3）特解为x=Bsin(ωt-ψ)，代入到式（3）。

经过一系列复杂推导，得到

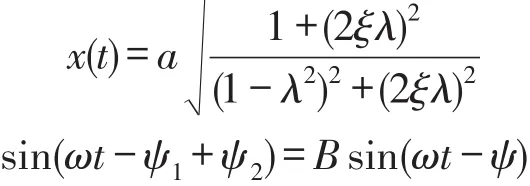
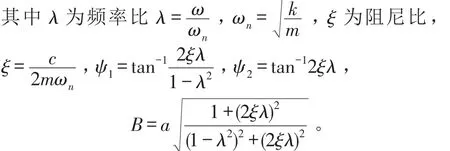
位移传递率β为

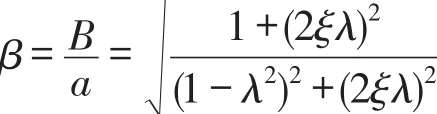
如果隔振器中没有设置阻尼器，即ξ=0，那么位移传递率为

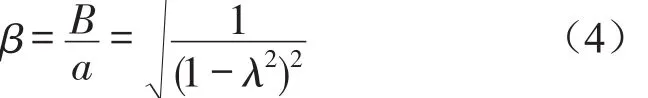
2 抗振支承结构设计

针对管道减振原理设计一种带有横向和轴向隔振功能的管道抗振支承，其三维结构图如图2所示。

图2 抗振支承结构图

管夹上盖4和底座5通过螺钉将管道固定住，管道横向方向上，主要通过四个弹性支撑组件2实行垂直方向上的隔振，四个弹性组件由三块120度错开分布的弹簧片和一个垂直方向安装的弹簧组成，其中一个弹簧片通过螺栓与底板1相连，其余两个弹簧片底部自由，当受到垂直方向的作用力时，弹簧片受压变形提供反作用力，同时中间的弹簧也起辅助支承。管道轴向方向上，由四个轴向布置的弹簧3实现轴向的隔振功能，当基础受到轴向的振动时，底板会带动四个支承和与之相连轴向布置的梁轴6振动，由于连接管道的底座与梁轴为间隙配合，管道在轴向上主要由四个轴向布置的弹簧约束，基础的振动会通过弹簧减振后传递到管道上，从而达到抗振目的。

3 抗振支撑弹簧片参数选择

上述设计的抗振支承结构需要根据减振对象所处的振动环境来选择其弹簧片参数，为说明其选择过程，以某段TBM液压管道为列，设定系统各参数值如下。

表1 管道系统参数设置

由表1的管道结构参数值可以得到管道和油液的总质量为m=3.816 kg，并初步设定横向减振目标为位移传递率β=0.2。

根据某TBM施工现场对振动信号的测试报告，分析得到振动参数的范围和分配情况，结果如表2所示。

表2 基础振动参数表

由表2可知，基础振动主要频率ω介于100 Hz～800 Hz之间。仿真时，取基础振动频率ω= 250 Hz。为了使抗振支承不过于复杂，这里不考虑设置阻尼器。通过化简得到弹簧刚度k=βm1ω2/(1+β)。其中m1并不等于管道和油液的总质量，由抗振支承的结构图2可知，管道由两端支承中八个小的弹性组件进行支承，因此m1=m/8。计算得到其弹簧刚度值为k=4 968N/m。

对于图2所示支承组件的三个弹簧片，可认为其是一端固定的矩形截面梁。由材料力学小挠度知识可得

其中k=Ebh3/(4l3)，E为弹簧片的弹性模量，且E=2.01×1011Pa，l为轴梁的长度，h和b分别表示弹簧片的厚度和宽度。

设弹性组件受到垂直向下集中力Fn作用，则单个弹簧片的受力为Fn/3，并在水平方向出现的变形量为x。经过推导得自由端Fn与变形量x的关系：

试选弹簧片尺寸如下：

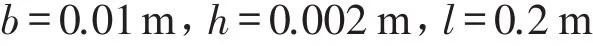
代入到式中（5），得到力Fn随变形量x的变化规律，结果如图3所示。

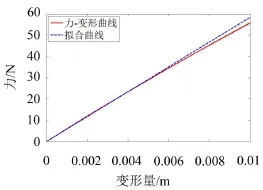
图3 力Fn随变形量x的变化规律

由图3可知，力和变形呈非线性关系，对处于小基础振幅下的弹簧片而言，其变形小，可以用一条直线去拟合小变形区域的线段，用这条直线的斜率来近似代替其小变形时的弹性系数。则在该弹簧片尺寸条件下，弹簧近似刚度值为k′=5 850N/m。与要求的弹簧刚度k=4 968N/m的误差为17.7%。误差较大，则该试选弹簧片结构尺寸不合格，需重新选择弹簧片结构尺寸。

用单因素法分别分析弹簧片的宽度、厚度和轴梁长度对近似弹性系数影响规律，结果表明：弹性系数与弹簧片宽度呈线性正相关；弹性系数随弹簧片厚度增大而增大，且其增长率越来越大；随着轴梁长度的增大，弹性系数减小。可见，改变弹簧片结构的尺寸能很方便调整其弹性系数。因此在设计时，可以根据所需的弹性刚度合理设计弹簧片的结构参数。

根据弹性刚度k=4 968N/m的要求，重新设计弹簧片，结构参数如下：

代入式（5），得到力Fn随变形量x变化规律，如图4所示。

由图4得到近似弹性刚度k′=5 250N/m与要求的弹性刚度的误差为5.6%，在10%误差范围内，满足要求。

然而，这只是在基础振动频率为ω=250 Hz、位移传递率为β=0.2时弹簧片的结构尺寸。

随着基础振动频率和位移传递率的不同，所需的刚度系数有很大的区别，其值随着基础振动频率或位移传递率的增大而增大，但随基础振动频率变化时的增加率呈现增大的趋势，而随位移传递率的变化其增长斜率减小。

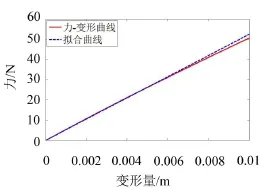
图4 力Fn随形变量x的变化规律

因此，在设计此种抗振支承的结构时，要充分考虑其所处的振动环境，并根据需要确定位移传递率，再计算得到所需的刚度值。该新型管道抗振支承的结构设计流程如图5所示。

图5 新型管道抗振支承结构设计流程

4 仿真分析

4.1 仿真模型建立

4.1.1 基础振动下管道横向振动微分方程

对管道单元和流体单元进行受力分析，运用达朗伯原理，得到输流管道在强振动环境中的横向振动非线性微分方程

其中L为管道长度，a为管道黏弹性系数，M为单位长度流体质量，U为流体流速，m为单位长度管道质量，͂为管道有效横截面积，A为管道过流截面积，EI为管道抗弯刚度，T0为轴向力，P为流体压强，ν为泊松比，g为重力加速度，t为时间，x为管道截面积的位置坐标；y为管道横向振动时的变形，且y＜＜L。

4.1.2 基础振动下管道轴向振动微分方程

输流管道系统耦合振动的研究方法中最流行的为4-方程模型。在已有模型的基础上，考虑轴向基础振动Nz=N1sinω1t，且水平液压管道θ=0o，重新推导适用于振动环境下TBM液压管道的流固耦合四方程模型。

式中P和V分别是流体压力和流速；uz表示管道轴向速度；E和ν分别是管道弹性模量和泊松比；e为管壁；ρf和ρp分别为流体密度和管道密度；σz是轴向应力；K表示流体体积压缩模量，R为内半径；θ为管道水平角度，τ0为切应力

其中λ为达西摩阻系数；Vrel=V-uz。

4.2 实例分析

某驱动液压系统中液压管道内径为0.02 m，管壁厚度为3 mm，管道总长为2 m，管道两端各设置一个支承，并处于横向、轴向基础振动频率ω=100 Hz、幅值a=2 mm的振动环境中，钢管密度为7 895 kg/ m3，液压油密度为890 kg/m3，支撑组件弹簧片的弹性模量E=2.01×1011Pa，要求减振装置的位移传递率为β=0.3。

长管道有2个支承，每个支承由4个支撑组件组成，先算出单个支撑组件的支撑刚度

轴向四个弹簧的弹性系数也为

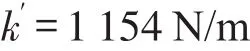
通过反复调整和优化逐步确定弹簧片最合理的结构尺寸。经计算最终确定其结构参数如下：

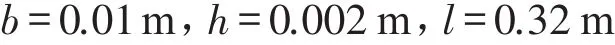
代入式（5），得到力Fn随变形量x的变化规律，得到小范围内变形的刚度近似为k′=1 260N/m。与所需弹性刚度的的误差为9.2%。

增加减振支承以后，管道最大应力点的动应力响应跟使用减振支承前的响应曲线对比如图6所示。

图6 减振前后应力响应对比

由图6可知：使用管道抗振支承前管道最大应力约为70 MPa，应力变化幅值约为19.5 MPa，使用后管道最大应力约为6 2MPa，应力变化幅值约为9.5 MPa，使用管道抗振支承后管道应变最大值和波动幅值分别减小了11.43%、51.28%。充分表明管道抗振支承能有效减小管道应力。

5 实验验证

设置振动台参数：振动幅值为2 mm，振动频率为100 Hz，设置PLC控制柜调节管道内油液压力，使之等于20 MPa，流量为84 L/min（流速为5 m/s），对管道应变进行采集。受振动台振动面尺寸的限制，采用支撑间距为1 m的管道。

图7（a）为振动幅值等于2 mm、频率为100 Hz时普通支承固定的液压管道固定支撑端应变的实验测试结果。由图可见管道应变随着管道的振动也呈现波动状态，但大部分波峰值在608个微电压附近，考虑采集时的放大倍数、微电压和应变的关系以及应力与应变的换算关系σ=Eε，计算得到应力约为63.9 MPa，少数峰值因干扰信号的影响而偏大或偏小。

将管道抗振支承安装到测试试验台上，设定振动台振动参数如下：频率为100 Hz，幅值为2 mm。采集管道固定支撑端应变的时域响应，结果如图7（b）所示。

图7 安装普通支承与抗振支承固定的管道应变时域响应

从图7（a）、图7（b）可以看到，装上抗振支承后管道应力明显降低，但由于振动时支承各部分组件之间的摩擦、冲击、弹簧片的非线性变形以及其他干扰信号的存在，应力波动的不规则性增强，大于平均峰值的点变得更多。

试验结果中波峰平均值约为518个微电压，与普通卡箍约束下的试验结果（608个微应变）相比减小了14.80%，通过管道横向振动微分方程得到平均波动幅值由18.25 MPa变为10.86 MPa，减小40.49%，充分表明管道抗振支承能有效减弱基础振动对管道应力的影响，此种新型支承对管道振动的隔离是真实有效的。

6 结语

（1）设计一种新型的适用于管道轴向与横向减振的抗振支承，结构简单、安装方便。

（2）该抗振支承能有效减小管道的应力和流体波动，使用抗振支承后管道应变最大值和波动幅值分别减小14.80%、40.49%。

[1]ZHANG KAIZHI,YU HAIDONG,LIU ZHONGPO,et al. Dynamic characteristic analysis of TBM tunnelling in mixed-face conditions[J].Simulation Modelling Practice and Theory,2010,18(7):1019-1031.

[2]鲁丽，杨翊仁.流体和结构参数对板-流体耦合振动的影响[J].西南交通大学学报，2009，44(3)：370-374.

[3]张振华，吴梵，冯文山.载流管道在基础振动下的振动控制[J].海军工程大学学报，2001，13(06)：84-85.

[4]王宇，樊洪海，张丽萍，等.高压气井完井管柱系统的轴向流固耦合振动研究[J].振动与冲击，2011，30(6)：202-207.

[5]赵子琴，李树勋，徐登伟，等.管道振动的减振方案及工程应用[J].管道技术与设备，2011，(3)：55-56.

[6]杜冬菊.潜艇水平舵液压管道减振降噪研究[D].青岛：中国海洋大学，2003：56-58.

[7]谢敬华.盾构液压系统流固耦合长管道效应研究[D].长沙：中南大学，2014：48-71.

[8]曾胜，任意，程涛涛，等.利用调谐质量阻尼器进行管路系统减振[J].振动、测试与诊断，2012，32(5)：823-826.

[9]HINY W,WIEDERMAN A H.A method for suppression of pressure pulse in fluid-filled piping,part:theoretical analysis[J].Journal of Pressure Vessel Technology, 1988,114(1):60-65.

[10]YAU C H,BAJAJ A K,NWOKAH O D.Active control of chaotic vibration in a constrained flexible pipe conveying fluid[C].Proceedings of the Winter Annual Meeting of the American Socitey of Mechanical Engineers,Anaheim, California,1992-11.Now York:ASME,1992,DE-Vol.50, AMD,144.93-108.

[11]SEMLER C,LI G X.PAIDOUSSIS M P.The non-linear equations of motion of pipes conveying fluid[J].Journal of Sound and Vibration,1994,169(5):577-599.

Research on a New Type ofAnti-vibration Supports for Hydraulic Pipelines

XIONG Yu1,ZHANG Huai-liang1,2,PENGHuan1
(1.State Key Laboratory of High Performance and Complex Manufacturing,Central South University, Changsha 410083,China; 2.College of Mechanical and Electrical Engineering,Central South University, Changsha 410083,China)

Based on the principle of the pipeline vibration damping,a new type of damping supports is designed for pipeline’s axial and transverse vibration damping.This type of hydraulic pipeline supports has the advantages of simple structure and easy installation.The vibration energy of the pipeline can be absorbed by the spring.The mathematical model of the hydraulic pipeline is established for vibration analysis.Through the numerical simulation,the fluctuation responses of the pipeline stress before and after the installation of the anti-vibration supports are analyzed and verified by testing.The results show that the anti-vibration supports can effectively reduce the pipeline’s stress and fluid pressure fluctuation.The maximum stress and the amplitude of the fluid pressure fluctuation of the pipeline are reduced by 14.80%and 40.49% respectively.The results of this research provide a theoretical basis for anti-vibration analysis of the pipelines on vibrating foundations.

vibration and wave;foundation vibration;hydraulic pipeline;anti-vibration support;pressure fluctuation

TH113

A

10.3969/j.issn.1006-1355.2017.02.034

1006-1355(2017)02-0168-05+177

2016-09-23

国家重点基础研究发展计划资助项目（973计划，2013CB035400）

熊宇（1992－），男，湖南省张家界人，硕士研究生，研究方向为液压元件动力学。

张怀亮，男，长沙市人，教授，博士生导师。E-mail:zhl2001@mail.csu.edu.cn