基于传递函数模型的白银价格分析与预测

（湖北师范大学 数学与统计学院，湖北 黄石 435002）

基于传递函数模型的白银价格分析与预测

余云彩，刘 玲，胡宏昌，肖劲光

（湖北师范大学 数学与统计学院，湖北 黄石 435002）

本文基于纽约商业交易所（COMEX）公布的2008年1月至2015年4月白银和黄金月收盘价数据，建立反映黄金与白银价格动态变化的传递函数模型，并与2015年5月至2016年2月的真实值进行比较分析，结果显示，传递函数模型的预测效果明显优越于回归模型和ARIMA模型，最后用传递函数模型对2016年2月之后10期白银月末收盘价进行预测，为白银产业链条企业及相关投资者提供参考与决策。

白银价格；传递函数模型；回归模型；ARIMA模型；预测

一、引言

明朝嘉靖八年（1529）白银正式成为法定货币，直至1935年国民党政府放弃银本位制，至此存续了406年。同黄金的强金融属性相比，白银逐渐褪下货币光环，成为名副其实的商品。那么，今时今日的“商品”白银和“金融”黄金之间的价格是不是完全脱钩了呢？这里面蕴藏着两层含义：一是黄金与白银二者之间的价格是否存在较强的相关性；二是黄金价格变动与白银价格的变动是否还存在很强的相关性。樊元等（2012）指出黄金与白银价格的变动方向与趋势基本一致，并建立了反映两者关系的回归方程。Christian Pierdzioch等（2015）用剩余增广最小二乘（RALS）检验黄金和白银价格的协整关系，结果表明两者没有长期的协整关系。李燕平等（2015）用VAR模型研究了白银价格的波动性，得出黄金价格对白银价格的波动影响最显著的结论。刘澄等（2007）考虑黄金和白银价格的线性比例，分析了两者的数理关系，并且建立了黄金价格与白银价格变动率的回归模型，但由于时间的可变性，使得这种方法有所局限。王维玮（2015）在分析全球白银供需状况的基础上，对白银价格进行了短期的宏观预测。本文基于黄金价格对白银价格有巨大影响，并且这种影响是动态的这一事实，选取纽约商业交易所（COMEX）公布的2008年1月至2015年4月白银（SI）和黄金（GC）的月收盘价，用黄金价格作为输入变量来研究白银价格这一输出变量，借助SAS软件建立反映黄金价格对白银价格动态影响的传递函数模型，并将回归模型、ARIMA模型和传递函数模型未来10年的预测结果与真实结果进行比较，从而对白银价格进行更准确的预测。

二、传递函数模型

ARIMA模型和回归模型在实际建模中发挥着重要作用。然而在实际中，一个时间序列未来的发展趋势不仅与自身过去的行为相关，而且还受另一个时间序列的影响，这使得ARIMA模型的应用受到限制，由于两序列之间的影响可能是同步的，也可能是滞后的，并且这种过程呈现出动态性，所以回归模型的结果也不尽人意。为了克服以上两种模型的弊端，本文引进由George E.P.Box和Gwilym M.Jenkins等提出的传递函数模型。

1、传递函数模型的原理

记时刻t的输入序列和输出序列分别为Xt，Yt，令

由于传递函数v（B）参数太多，并且计算过程冗杂，在实际中，我们用有理函数来近似表示：

其中，P（B）=1-ω1B-ω2B-…-ωsBs，Q（B）=1-δ1B-δ2B-…-δrBr，b表示Xt延后b期影响Yt，C为刻度参数，P（B），Q（B）分别是次数为s和r的滞后算子多项式。尤其当一个序列对另一个序列的影响同步（即b=0时），实际应用的传递函数模型可以写成如下形式：

2、传递函数模型的建立

传递函数模型的建立有预白噪声化和最小平方两种方法，本文用预白噪声化法，具体步骤如下：第一步，识别输入序列的适应性模型，并对其预白噪声化。第二步，计算两序列平稳化后的交互相关函数，识别初步传递模型。第三步，鉴别初步传递函数模型残差的白噪声性，确定最后的传递模型。

三、白银价格传递函数模型的建立

1、数据来源与描述

2018年7月22至29日在美国路易斯安纳州新奥尔良市举行了“新奥尔良国际钢琴比赛”。比赛结果如下：获得第一名的是中国的Ziang Xu；获得第二名的是韩国的Sung Chang；获得第三名的是韩国的Jae Weon Huh。此外，共有12位选手参加最后的决赛。

本文选用纽约商业交易所（COMEX）公布的2008年1月至2015年4月白银（SI）和黄金（GC）月收盘价，记Yt为t月份的COMEX白银月末收盘价，Xt为t月份的COMEX黄金月末收盘价。

图1、图2显示黄金价格Xt和白银价格Yt均呈现先上升后下降的趋势，并且两者呈现出非常强烈的正相关性。在这近8年间，有两个阶段比较引人关注：其一，2008年金融危机爆发，国际经济大幅下滑，白银价格有所下滑，黄金价格亦有小幅度下降。此后，黄金由于其储备货币及避险功能，价格大幅上涨，而白银价格持续低迷。其二，2010年至2011年，白银价格暴涨，一度接近其历史最高值，而黄金价格也持续上涨，但增长速率比白银价格要慢。2012年至2015年，国际经济复苏，美元价格回升，白银价格回落。

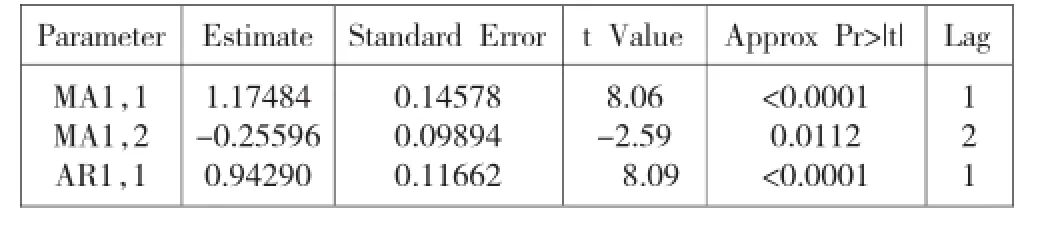
表1 ▽Xt模型的参数估计

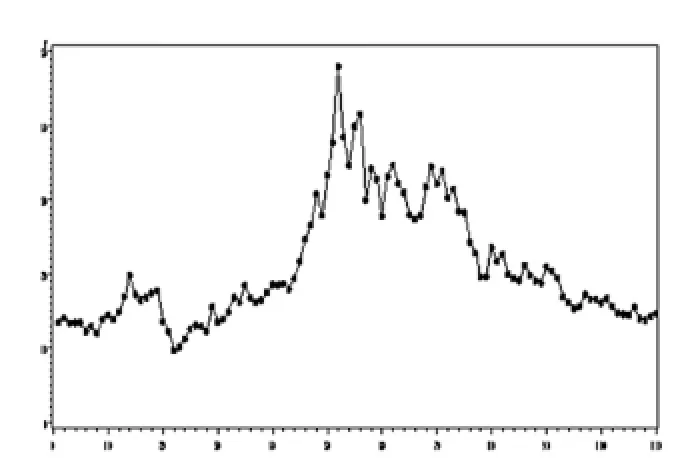
图1 黄金价格Xt时序图

图2 白银价格Yt时序图

表2 ▽Xt模型的残差白噪声检验

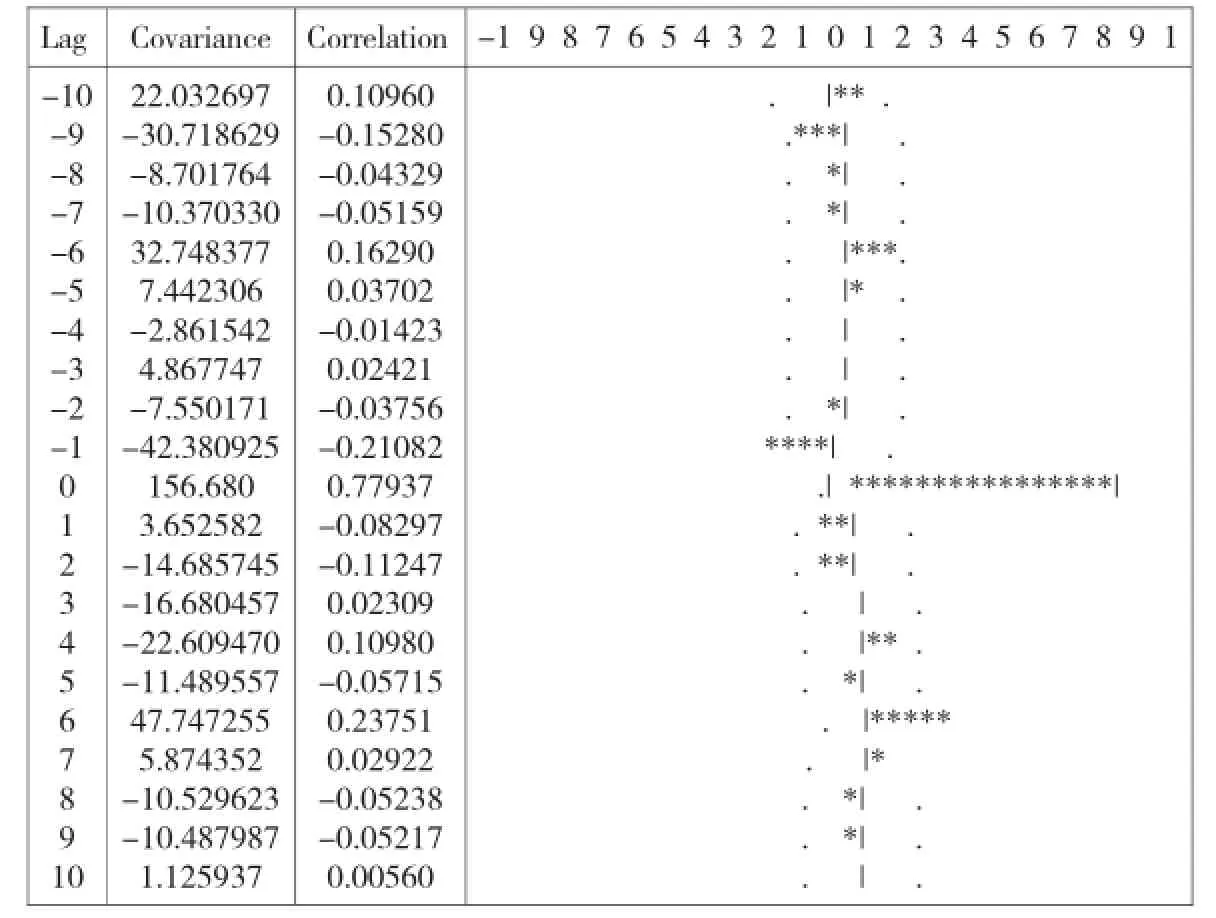
表3 ▽Xt与▽Yt的交互相关函数

表4 初步传递函数模型的参数估计

表5 初步传递模型残差的白噪声检验

表6 输入序列▽Xt与模型残差at的交互相关性检验

表7 Yt序列ARIMA模型的参数估计

2、建立传递函数模型

（1）识别Xt的适应性模型，并进行预白噪声化。由黄金和白银价格的时序图可看出其不平稳性，我们对两序列同时进行一阶差分，令▽Xt=Xt-Xt-1，▽Yt=Yt-Yt-1。

由表1和表2可知，▽Xt的适应模型为ARMA（1，2），

其中，序列at为白噪声序列。

（2）计算▽Xt与▽Yt的交互相关函数，识别初步传递模型。从表3可以看出，▽Xt和▽Yt的样本互相关函数在延迟0阶处显著不为零，说明▽Xt对▽Yt的影响是同期的，即b=0，我们取s=2，k=2提出如下模型：

根据表4，初步传递函数模型可写成：

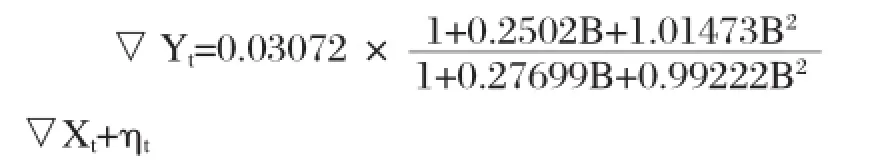
（3）检验ηt的白噪声性，确定最后的传递模型。由表5知，0.0511＞0.05，表明前面建立的传递函数模型残差at显著平稳，可认为是随机白噪声序列。由表6知，互相关函数显著为零，输入序列▽Xt与模型残差at相互独立，模型有效。最终得到的传递函数模型为：

四、传递函数模型与ARIMA模型、回归模型预测效果的比较

从形式上，传递函数模型可看作ARIMA模型与回归模型的结合，为了检验传递函数模型的预测效果，本文对单个序列Yt建立了ARIMA模型，并对Xt和Yt序列建立了回归模型。

1、ARIMA模型

由于本文研究的重点是传递函数模型，所以建立ARIMA模型的具体过程此处省略，最终模型建立如下：

表8 Yt序列ARIMA模型残差白噪声检验

表9 回归模型的参数估计

表10 三种模型与真实值的比较

表11 传递函数模型对2016年3月至2016年12月白银价格的预测

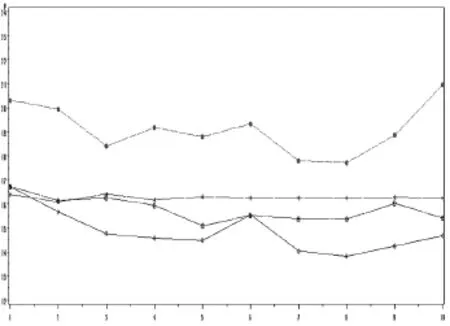
图3 三种模型的预测结果与真实值的比较图

其中，εt是白噪声序列。

表7显示，白银价格Yt序列拟合的ARIMA模型参数显著。表8表明Yt序列拟合的ARIMA模型残差为白噪声，模型可用于预测。

2、回归模型

根据刘澄等（2007）建立回归模型的方法，视Xt为自变量，Yt为因变量，先去除COOK距离大于0.04的强影响点（第51，52，53，55，56个观测值），再用最小二乘估算回归参数，最终建立Yt与Xt的一元回归方程为：

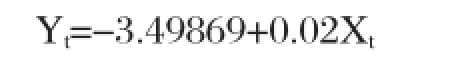
由表9可知，回归方程的参数显著，此结果与刘澄等（2007）建立的回归模型非常接近，可以用于对白银价格的预测。

3、三者预测结果与真实值的比较

为了评估传递函数模型的预测效果，我们将传递函数模型、回归模型、ARIMA模型对未来10期的预测结果与2015年 5月至2016年2月COMEX白银月收盘价真实值进行比较。

表10显示，在相对误差的意义下，传递函数模型的预测效果明显优于回归模型和ARIMA模型，所以笔者认为在对多变量时间序列建模时，使用传递函数模型更能准确把握未来发展趋势。图3则更直观地显示了传递函数模型优越的预测效果。

五、白银价格的分析与预测

黄金与白银价格两者之间存在相关关系，两序列一阶差分后平稳，并且交互相关系数显著为零，表明两者没有长期的协整关系。从拟合的结果来看，用黄金价格作为输入序列的传递函数模型在分析白银价格未来走势上具有很好的可信度。下面用传递函数模型对2016年3月至2016年12月的COMEX白银月收盘价进行长期的预测，由于建模过程跟之前的建模过程类似，此处略，预测结果见表11。

结果显示，2016年全球经济将仍处于修复期，上半年白银价格仍有继续下探的趋势，7—8月会降到全年的最低价，9月会有所上升，但是涨幅不是很大，10月会下跌，11—12月白银价格有所回升，但总体来看全年白银价格波动不大。

[1] Christian P.，Marian R.，Sebastian R.. Cointegration of the Prices of Gold and Silver：RALS-Based Evidence[J].Finance Research Letters，2015（15）.

[2] 李燕平、赵翔宇：基于VAR模型的白银价格影响因素分析[J].经济问题，2015，10（12）.

[3] 樊元、王群：黄金白银投资比较及价格影响因素分析[J].商业研究，2013，1（11）.

[4] 刘澄、张均东：国际黄金、白银价格变动的实证分析[J].特区经济，2007（12）.

[5] 王维玮：2014年白银市场分析及2015年市场展望[J].中国贵金属，2015（1）.

[6] 肖枝洪、郭明月：时间序列分析与SAS应用[M].武汉：武汉大学出版社，2009.

[7] 汪远征、徐雅静：传递函数模型在我国GDP数据分析中的应用[J].数学的实践与认识，2007，37（16）.

[8] 朱宗元、王秋霞：基于传递函数模型的我国社会消费品零售总额预测[J].统计与决策，2010，10（24）.

（责任编辑：刘冰冰）

国家自然科学基金项目，相依回归模型与扩散过程的统计推断及其应用，编号：1471105。