基于改进QR-PSO算法的压力传感器的动态补偿方法

魏 娟,张志杰,杨文杰,赵晨阳(中北大学仪器科学与动态测试教育部重点实验室,太原 030051)



基于改进QR-PSO算法的压力传感器的动态补偿方法

魏 娟,张志杰*,杨文杰,赵晨阳
(中北大学仪器科学与动态测试教育部重点实验室,太原 030051)

针对压力传感器在实际使用中动态特性难以满足测试需求这一问题,利用激波管对压力传感器进行动态标定,获取实验样本,依赖样本估计逆模型,提出了基于QR分解和改进粒子群算法构建补偿系统的设计方法。采用QR分解确定模型阶次,降低了简化传感器模型带来的动态补偿运算误差,并结合改进粒子群算法,高效、智能的确定补偿系数。通过实测样本对补偿系统进行重复性验证,结果表明压力传感器的动态响应性能显著地提高了,补偿效果令人满意。

压力传感器;QR分解;粒子群优化算法(PSO);动态补偿

在科学研究、测试计量、工业控制等研究开发领域,需要更多地结合动态测试,即深入、定量地测试和反应瞬态过程中各种参数的变化规律,同时对传感器的准确度、稳定性和抗干扰性提出了更高的要求[1-2]。但由于制作技术和工艺水平的限制,很难满足动态测量的需求。通过对传感器的动态特性进行补偿,可以提高传感器的响应速度、降低超调量、扩宽工作频带以达到动态测试需求[3]。

对传感器动态补偿方法多种多样,主要有两种:一是依赖传感器动态模型的动态补偿方法,如零极点配置法、反卷积法等,此方法需要确定传感器的动态模型,实现起来较为复杂[4]。二是不依赖传感器动态模型补偿方法,如本文中使用的粒子群算法,通过逆建模构建传感器补偿系统。粒子群算法(PSO)是一种随机全局优化算法,不依赖初始值,且具有较快速的收敛速度,但是在寻找最优解的过程中易受到补偿阶数的影响[5]。此处,利用传感器激波管标定的数据和实际理想输出,通过QR分解优先识别出补偿模型的阶数,再根据改进的粒子群算法进行求解得到补偿系数,构建补偿模型,改善传感器的动态响应特性。

1 压力传感器的动态校准

为得到压力传感器的动态性能指标,需要对压力传感器进行动态校准。激波管可以产生陡峭的上升沿、激波持续时间长、能够充分激励起传感器的动态特性,且具有可溯源性[6]。故常以激波管作为“理想”阶跃压力信号发生器对压力传感器进行标定,为补偿系统构建模型提供实验数据。

激波管可以产生上升沿小于1 μs、平台时间大于5 ms的阶跃压力信号,是理想的激励信号源。校准时,将压力传感器齐平安装在激波管端面。如图1所示,在激励信号的作用下,传感器产生响应信号,按照式(1)～式(3)对采集电路得到的测速传感器的响应数据进行处理,首先根据测速传感器之间的已知距离l,以及得到的输出信号波形计算出时间差t,激波入射速度v,求取马赫数Ma,计算待校准压力传感器感受到的反射激波的阶跃压力Δp。根据马赫数Ma和阶跃压力Δp的范围,可判断激波管所产生的阶跃信号是否理想,能否完全激励起待校准传感器;并判断用于建模的实测数据是否有效,能否为后续补偿系统构建模型提供有效、可靠的数据。

(1)

(2)

(3)

式中:aT为低压室的T℃时音速,β=0.003 66,p0为已知的低压室气压。

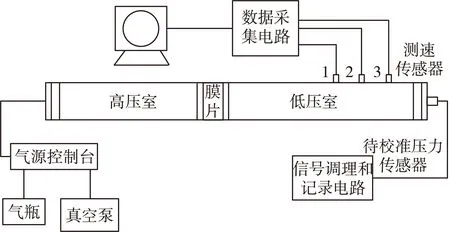
图1 激波管动态校准系统示意图

2 压力传感器动态补偿方法

以逆建模方式估计补偿模型,补偿原理如图2所示,在输出信号y后接补偿环节[7],达到扩宽传感器响应频带,提高传感器的响应速度等应用要求。

图2 传感器动态补偿示意图

图3给出基于改进PSO算法的传感器动态补偿的原理图。将传感器输出信号y(k)作为补偿系统的输入信号,“理想”阶跃信号r(k)作为参考信号,采用改进的粒子群算法构建补偿模型。根据得到的补偿系统参数构建符合要求的补偿滤波器,串接在原传感器系统之后,达到改善其动态特性的目的。

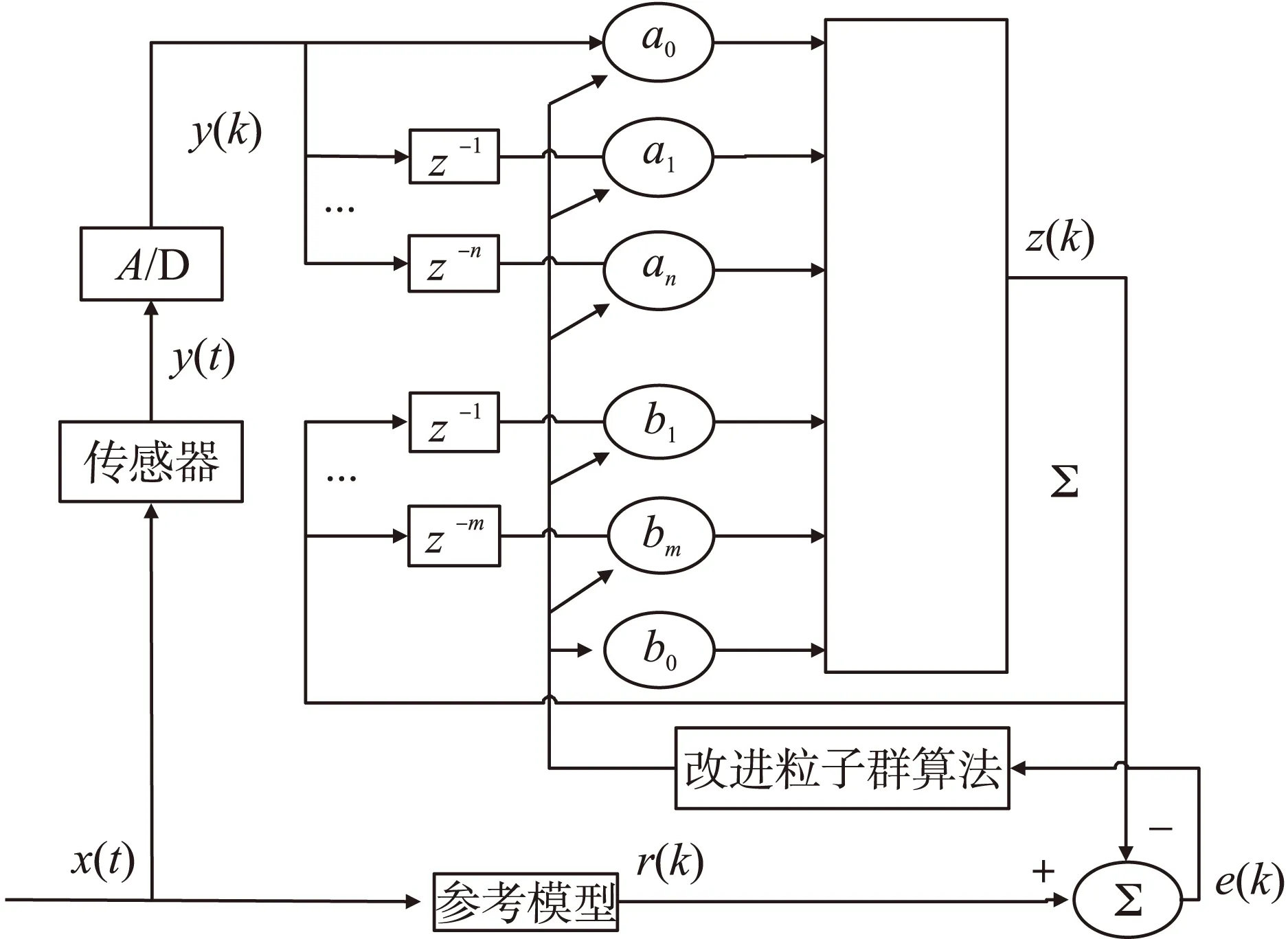
图3 传感器动态特性改善方法示意图

3 补偿模型建立

3.1QR分解确定模型阶次

对传感器的动态模型参数辨识前,需要先对模型的阶数进行确定。压力传感器一般等效为二阶系统,但在输入信号的激励下,输出信号在谐振点处容易发生震荡,引入动态误差[8]。为获得更好的补偿效果,通常将传感器阶数设置为较高阶次,但同时增加了设计的工作量且改善效果并不能明显提高。因此需要对传感器模型的阶数进行严格的验证,选取合适的阶数,获取良好的补偿效果[9]。

最基本且应用较为广泛的系统辨识方法是最小二乘法,本文为了提高辨识的效率和辨识结果的数值稳定性,采用效率与精度较高的QR分解来实现[10]。

通常认为传感器系统为单输入单输出的线性时不变系统,系统的差分方程为

y(k)+a1y(k-1)+…+any(k-n)=b1u(k-1)+…+bmu(k-m)+e(k)

(4)

式(4)可写成

y(k)=θWT(k)+e(k)

(5)

式(5)中

W(k)=[u(k-n) …u(k-1),y(k-n) …y(k-1)]

(6)

θ=[bm…b1,an…a1]

(7)

即

A(z-1)y(k)=B(z-1)u(k)+e(k)

(8)

式(8)中:y(k)为实验测试数据,u(k)为理想阶跃信号,e(k)为输出误差。

本文通过对实验数据进行QR分解,求取残差平方和,判别合适阶数。构建实验数据矩阵D={(u(k),y(k))|k=1,2,…,N}

式中:v为待检验的阶数,N为数据长度,对矩阵进行QR分解,可以得到如下矩阵

式中:m=2v+2,R′是一个m×m维的上三角方阵。计算R′阵对角线偶元素平方和数值即为各阶差分方程模型对应于最小二乘法估计的残差平方和[11]。通过比较各阶模型残差平方和的大小,确定补偿模型适合的阶数。

3.2 改进粒子群算法(PSO)确定补偿系数

粒子群算法是一种基于群体智能的全局优化计算技术,具有高精度的稳定性、并行性和全局搜素能力[5]。其原理是n个粒子构成初始种群,每个粒子随机初始化一个速度,每个粒子都对应优化问题的一个解,由目标函数计算出适应度,每个粒子通过不断调整自己的速度和位置,更替自己的最优位置和全局的最优位置,逐步搜素,直到求取最优解。

在D维搜素空间,记第i个粒子的位置Xi=(xi1,xi2,…,xiD),速度为Vi=(vi1,vi2,…,viD),搜索到的历史最优位置Pbest=(pi1,pi2,…,piD),整个粒子群搜索到的最优位置Pg=(pg1,pg2,…,pgD),各个粒子按照下式更新其速度和位置。

vid(n+1)=wvid(n)+c1r1d(n)(pid-xid(n))+c2r2d(n)(pgd-xid(n))

(9)

xid(n+1)=xid(n)+vid(n+1)

(10)

式中:w为惯性权,c1,c2为加速系数,r1d,r2d为在[0,1]内均匀分布的随机数,n为当前迭代次数。但惯性权值w选取的范围影响算法的搜索能力,较大的权值有利于全局搜索,而较小的权值会提高局部搜索,此处采用线性递减权值(LDIW)策略,以在全局和局部搜索之间取得最佳平衡,且收敛速度快、相对简单[12]。LDIW策略中惯性权值按照下式进行更新:

(11)

式中:N为最大允许迭代次数,i为当前的迭代次数,当选取wstart=0.95,wend=0.4时,PSO算法的性能会显著提高,相对于基本PSO算法,它对大多数测试函数的应用具有收敛速度快且求解精度高的优点[13]。适应度函数采用均方误差值进行比较进行。公式如下:

(12)

式中:yi为预测值,ki为理想输出,N为样本数目。

根据QR分解和改进的粒子群算法,可以得到补偿滤波器传递函数的阶数和系数,构建补偿系统传递函数。

4 压力传感器补偿结果

根据激波管标定数据,得到实验测试样本,此处所用实测数据长度N为1 000,待检验的阶数v为16,结合构建的“理想”阶跃信号进行QR分解,得到补偿模型的最佳阶数。从图4中可以看出,残差平方和值在2阶处有明显下降的趋势,之后缓慢下降近似趋于稳定值。基于补偿效果和硬件实现难易程度的考虑,本次建模中选取8阶。

图4 残差平方和随阶数变化折线图

将实测数据作为观测样本,构建“理想”阶跃信号作为目标样本,通过改进的粒子群算法得到补偿滤波器的系数。此处所用数据的数据长度N为1 000,采样频率为1 MHz,粒子群训练次数为3 000,初始粒子的个数为30,设置好所需参数之后,对实测数据进行训练,得到的补偿滤波器的传递函数为:

H(z)=(1.4488+0.4246z-1+0.4194z-2+0.8071z-3+0.1774z-4+0.3252z-5+0.0094z-6-0.0476z-7-0.0808z-8)/(1.5713-0.0170z-1+0.8315z-2+0.7035z-3+0.0584z-4+0.5005z-5-0.1093z-6+0.0388z-7-0.0859z-8)

将得到的系数构建补偿滤波器模型,绘制补偿前后系统的幅频特性图如图5所示,补偿结果表明,有效带宽由补偿前的72 kHz,扩宽到210 kHz。高频噪声控制很好,没有扩大,且一定程度地减小了传感器谐振频率对输出信号的影响,动态特性得到了明显的改善。绘制补偿前后信号对比图如图6所示。

图5 补偿前后幅频特性图

图6中,补偿前的输出信号上升时间为2.6 μs,响应时间为0.3 ms,超调量为37%。补偿后的输出信号上升时间为2.4 μs,响应时间为8.5 μs,超调量降低到4%,可以明显看到输出信号的动态特性得到了明显的改善。

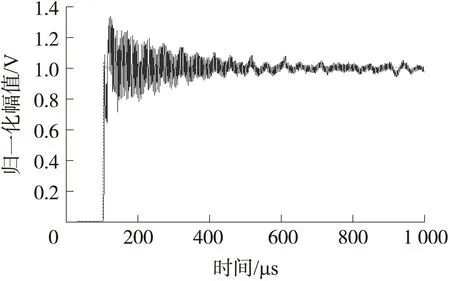
图6 补偿前后信号对比图

在用激波管对压力传感器进行动态标定的过程中,同一支传感器需要多次激励得到多组数据。为验证已建立补偿系统的改善性能,将同一支传感器的其余多组数据加载到补偿系统,得到补偿后输出信号图如图7,补偿后信号的超调量均由之前的40%左右降到了4%,响应时间由之前的0.3 ms左右改善到2.5 μs,上升时间均在2.6 μs左右,动态补偿结果明显。实验结果表明该补偿模型补偿效果明显,实用性强。

图7 多组数据补偿前后对比图

5 结论

压力传感器在使用过程中,存在响应频带不足,超调严重等问题,难以满足实际动态测试需求。为提高压力传感器的动态响应特性,本文根据激波管标定的实验数据,进行逆建模,构建补偿传感器补偿模型。依据简单、灵活的QR分解确定补偿滤波器的阶数,权衡补偿效果和硬件实现难易程度,选择合适的补偿阶数。利用改进粒子群算法计算补偿系统的系数,该方法具有快速收敛性和高精度,能在局部和全局中寻找最佳值。根据实验数据的仿真测试结果,可以看到补偿之后动态特性改善明显。该补偿模型实现简单,补偿精度较高,动态特性改善明显,易于硬件实现,可广泛应用于实际测试工程中。

[1] 朱照. 传感器动态特性模拟及动态补偿滤波器的DSP实现[D]. 太原:中北大学,2010.

[2] 郭士旭,余尚江,陈晋央,等. 压电式压力传感器动态特性补偿技术研究[J]. 振动与冲击,2016(2):136-140.

[3] 杨文杰,张志杰,赵晨阳,等. 基于零极点配置理论的压力传感器动态特性补偿[J]. 科学技术与工程,2016(2):78-82+99.

[4] 轩春青,轩志伟,赖富文. 压力传感器测试系统的动态校准及特性分析[J]. 传感技术学报,2015,28(7):982-986.

[5] 赖富文,张志杰,张建宇,等. 基于动态特性补偿的冲击波测试数据处理方法[J]. 爆炸与冲击,2015(6):871-875.

[6] 刘一江,孟立凡,张志杰,等. 冲击波测试系统中传感器动态补偿装置[J]. 传感技术学报,2012,25(11):1516-1521.

[7] 刘砚. 基于模糊逆模型的自适应逆控制及其应用研究[D]. 燕山大学,2012.

[8] 戴先中,殷铭,王勤. 传感器动态补偿的神经网络逆系统方法[J]. 仪器仪表学报,2004(5):593-596.

[9] 轩春青,轩志伟,陈保立. 基于最小二乘与粒子群算法的压力传感器动态补偿方法[J]. 传感技术学报,2014,27(10):1363-1367.

[10] 孙延鹏. QR分解技术在递推系统辨识中的应用[D]. 北京:北京交通大学,2008.

[11] 黄俊钦. 测试系统动力学[M]. 北京:国防工业出版社,2013:12.

[12] 刘杨,田学锋,詹志辉. 粒子群优化算法惯量权重控制方法的研究[J]. 南京大学学报(自然科学版),2011,47(4):364-371.

[13] 吴健. 传感器动态补偿滤波器及其硬件实现方式研究[D]. 太原:中北大学,2012.

魏 娟(1993-),女,山西运城人,硕士研究生,主要从事动态测试,动态信号的实时获取、存储与处理,18234040047@163.com;

张志杰(1965-),男,山西五台人。现任中北大学教授、博士生导师,仪器科学与技术学科带头人之一,主要从事动态测试理论、技术与应用,信号处理理论与技术的研究。教育部仪器科学教学指导委员会协作委员,zhangzhijie@nuc.edu.cn。

The Dynamic Compensation Method Based on Improving QR-PSO Algorithm for Pressure Sensor

WEI Juan1,ZHANG Zhijie*,YANG Wenjie1,ZHAO Chenyang
(Key laboratory for instrumentation Science and Dynamic Measurement,Ministry of Education,North University of China,Taiyuan 030051,China)

Aiming at the problem that the dynamic characteristics of the pressure sensor can not meet the requirements of the test in practical application,using the shock tube to calibrate the pressure sensor dynamically,obtain the experimental samples,and then estimate the inverse model. A design method of constructing compensation system based on QR decomposition and improving particle swarm optimization(PSO)algorithm.The QR decomposition is used to determine the order of the model,which reduces the dynamic compensation operation error caused by the simplifying the sensor model,combined with the improved particle swarm optimization algorithm,the compensation coefficient is determined efficiently and intelligently. By verifying the repeatability of the compensation system through the measured samples,the experimental results show that the dynamic response of the pressure sensor is improved significantly and the compensation effect is satisfactory.

pressure sensor;QR decomposition;particle swarm optimization(PSO)algorithm;dynamic compensation

2016-09-30 修改日期:2016-12-09

TP212.6

A

1004-1699(2017)04-0550-05

C:7230;7220

10.3969/j.issn.1004-1699.2017.04.011