一种基于迭代优化的安全定位算法*

滕 云,刘宏立(湖南大学电气与信息工程学院,长沙 410082)



一种基于迭代优化的安全定位算法*

滕 云,刘宏立*
(湖南大学电气与信息工程学院,长沙 410082)

由于无线传感网络节点往往部署在恶意环境中,节点不能获得准确的位置信息,导致网络运行的安全性受到破坏。针对无线传感网络在恶意环境中的安全定位问题,提出了一种新的基于牛顿迭代法的安全定位算法。首先建立了安全定位模型,然后对迭代过程中梯度矢量进行了分析,并且利用差分阀值法改进和优化了按百分比过滤的异常检测过程,最后通过剩余锚节点信息和牛顿迭代法对未知节点实现高精度定位,进一步提高了节点定位精度。仿真结果证明,牛顿迭代法在定位应用上优于梯度下降法,并且优化后的安全定位算法具有更好的定位精度和鲁棒性。

无线传感器网络;安全定位;牛顿迭代法;异常检测;差分阀值法;

随着网络技术和无线通信技术的迅猛发展,无线传感网络[1]WSN(Wireless Sensor Network)成为了当今炙手可热的信息获取和处理技术。因为其具有功耗低,组网快捷的特点而被运用到很多的民用和军事领域,它在定位方面更是具有价格低廉,定位精准,布置网络方便,无需维护的特点,使其被广泛的应用各个方面,如森林防火,海洋探测,军事监测[2],环境监控[3]等。

目前的WSN节点定位算法主要分为两类:距离无关(range-free)的定位算法[4]和基于距离(range-based)的定位算法[5]。range-based定位算法由于定位精度高,得到了研究人员的广泛关注。到达时间(ToA)[6]、到达时间差(TDoA)[7]、到达角度(AoA)、和接收信号强度(RSSI)[8]是最常用的测距技术。基于RSSI的定位算法由于实现简单、无需额外的硬件设施而被广泛的应用。但是,由于WSN一般部署在无人值守的区域,传输信道的广播特性,使其很容易受到攻击者的各种恶意攻击,使网络中的节点不能够准确的定位

对于在恶意环境下的无线传感网络安全定位问题,研究人员已经从不同的方面提出了一些传感器节点定位的安全策略[9],如有的方法采用一系列的包括时间、空间和一致性的检验技术来抵御针对距离的欺骗攻击[10]。文献[11]针对WSN定位中遇到的独立攻击,结合最速下降法和牛顿迭代法提出了一种抗独立攻击的安全定位算法,通过恶意锚节点检测技术和最速下降法选出最优锚节点数据,并利用牛顿迭代法实现了快速高精度的三维安全定位。文献[12]提出了一种名为BRS的安全定位算法,使用信誉系统筛选锚节点,并利用加权泰勒展开式的最小二乘算法来获得最终的定位位置,该算法有效的减轻了恶意锚节点对网络节点定位的影响。但是利用信誉机制筛选锚节点会给网络节点带来很大的能量消耗,影响了网络运行效率。文献[13]根据统计方法提出了基于最小二乘法和最小中位数二乘法算法,通过基于中值距离的测量和计算方式,容忍WSN中对定位的恶意攻击。

本文提出的安全定位算法是一种过滤算法,结合牛顿迭代和优化的异常检测方式,根据梯度矢量的差分阀值过滤掉网络中的恶意锚节点,对未知节点进行高精度迭代定位。本文对文献[14]提出的异常检测的过滤方式进行了改进,利用差分阀值取代了该文献中的根据百分比过滤的方式,并且使用了定位性能更好的牛顿迭代法进行定位计算。由于过滤算法方式的改进和定位方法的不同使得在定位精度上有一定区别,仿真结果表明本文所提出的算法能得到更好的定位精度。

1 安全定位模型

假设一个部属在二维空间R2的无线网络,网络中有n个锚节点和一个目标节点,锚节点位置已知,其坐标可以表示为(xi,yi);目标节点u位置未知,其坐标为(x,y)。假设目标节点能够和所有的锚节点之间进行通信,每个锚节点都会发送一个包含自身位置信息和ID的信标报文给目标节点,目标节点接收到这些信息后,采用一定的定位算法计算出自己的位置信息。令这些锚节点分别为M1,…,Mn,在这n个锚节点中,部分锚节点可能是恶意锚节点,这些恶意锚节点会发送错误信标和位置信息给节点N,而诚实锚节点完全按照定位协议如实地发送自己的信息给节点N。令k表示恶意锚节点的数目,并且网络无法预知k的大小。

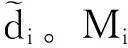
(1)

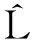
(2)

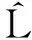
(3)

那么,定义代价函数

(4)

可以证明λ(L)是一个凸函数,因此,定位问题就等价于寻找使代价函数λ(L)达到最小值的点L0。

2 基于迭代的安全定位算法

2.1 基于牛顿迭代安全定位算法

针对上述安全定位模型分析,λ(L)是一个凸函数,这个凸性使得其能够使用牛顿迭代法对式(4)求取非线性最小值点。设第k次迭代以后得到的估计坐标为L(k),在L(k)处将代价函数λ(L)按二阶泰勒级数展开

(5)

式中:右上角的H表示埃尔米特转置。求解第k次的梯度向量

(6)

gi(k)是第i个锚节点对应的梯度矢量,对代价函数求解二阶偏导,

(7)

得到的H(k)是L(k)处代价函数λ(L)的海森矩阵。式(5)对L求导并令导数为零,可求出下一个迭代结果为

L(k+1)=L(k)-H-1(k)g(k)

(8)

式中:H-1(k)是海森矩阵H(k)的逆矩阵。这个迭代方程就是最优化理论中牛顿法迭代公式。

根据牛顿迭代理论可以证明,经过少量的迭代以后,牛顿迭代计算估计值收敛于LS解。当网络中存在一部分锚节点是恶意锚节点时,所得到的LS解就不准确。恶意锚节点的数目越多,所估计位置的误差就越大。因此仅仅通过牛顿迭代运算不能在恶意环境下得到理想的节点估计值,需要利用异常检测找出网络中的恶意锚节点,并且将其滤除掉才能极大减小恶意攻击对定位的影响。

2.2 异常检测

异常检测是为了减少恶意攻击对定位精度的影响。图1表示了一个包含3个锚节点的异常检测过程,当梯度向量‖g(k)‖小于预先设定的门限阈值时,梯度矢量模值‖gi(k)‖大的锚节点会被认为是恶意锚节点而被滤除掉。设{‖g1(k)‖,…,‖gi(k)‖,‖gi+1(k)‖,…,‖gn(k)‖}是关于力矢量的从小到大的有序排列,若对于某一个i,有‖gi+1(k)‖-‖gi(k)‖>β,其中β为差分阈值,则去除{‖gi+1(k)‖,…,‖gn(k)‖}的所有力矢量,用剩余的力矢量计算梯度g(k),再根据式(8)进行下一步迭代。按照力矢量模值的相对大小以及差分阈值β的选择来对恶意锚节点进行过滤。

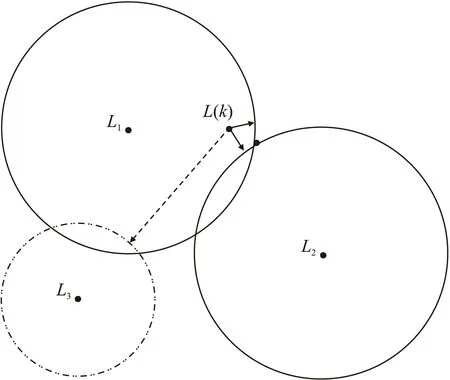
图1 异常检测过程示意图

3 性能分析

为了分析牛顿迭代算法在定位中的性能,针对3个参数对牛顿迭代法和梯度下降法进行比较。控制仿真参数的一致性,仿真条件参照文献给出:30个锚节点随机分布在大小为60 m×60 m的区域中,测量噪声标准差η=2 m,梯度向量模值门限阈值为0.9,初始迭代点L‖0‖在区域中随机选取,恶意锚节点数占总锚节点数的30%,即9个恶意锚节点。所有的仿真结果都通过1 500次运行取平均值得到,异常检测阶段去除50%的锚节点。

图2 牛顿迭代法平均迭代次数曲线

收敛速度是迭代运算中至关重要的参数,因为它决定了运算效率,特别是应用在WSN中时,计算效率越高,整个网络的工作效率就越高。于是仿真了牛顿迭代法在不同攻击强度下的平均迭代次数。从图2可以看到,该方法收敛时的迭代最大次数不超过18次。而文献[15]仿真显示梯度下降法需要200次迭代才能收敛,因此牛顿迭代法的收敛速度非常快,计算效率是梯度下降的10倍。

第2个参数是定位误差。从图3可以看到,不论攻击强度多大,牛顿迭代法的定位误差都小于梯度下降法。

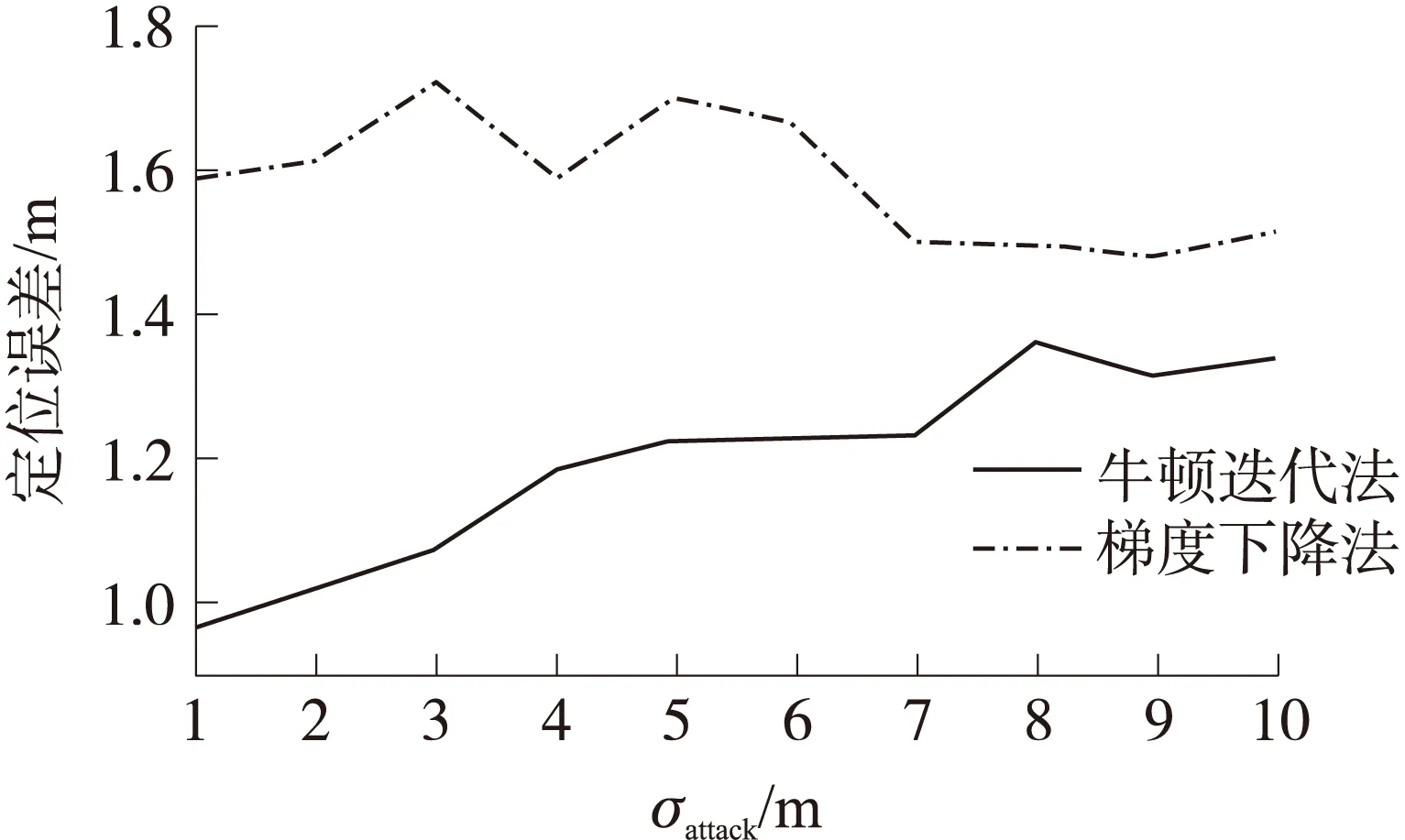
图3 攻击强度与定位误差关系图

由于在迭代计算的过程中,有可能出现不收敛的情况,这种情况会使得最后的计算结果误差相当大,因此稳定性也是影响定位的重要参数。最后仿真了在攻击强度σattack=10 m的条件下,牛顿迭代法和梯度下降法1 500次的平均定位误差。图4可以看出,牛顿迭代法的收敛概率近似为1,而梯度下降法有时会出现很大的定位误差。因此,梯度下降法的收敛性不能得到保证,其稳定度较差,而牛顿迭代法的稳定性更好。

图4 定位误差蒙特卡洛实验曲线(σattack=10 m)

差分阈值β的大小选择会直接影响定位误差的大小,图5显示了差分阈值β的大小与定位误差的关系。从图中可以看到,差分阈值β与定位误差曲线大致呈抛物线形,β=1.5时定位误差最小。

图6表示出了基于差分阈值异常检测和固定百分比异常检测的比较结果。从图中可以明显看到,不论从攻击强度还是恶意锚节点数来看,基于差分阈值的异常检测结果都明显好于固定百分比异常检测结果。

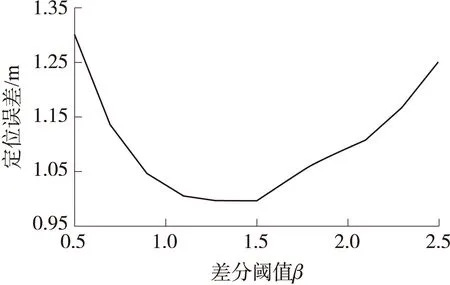
图5 差分阈值与定位误差关系图

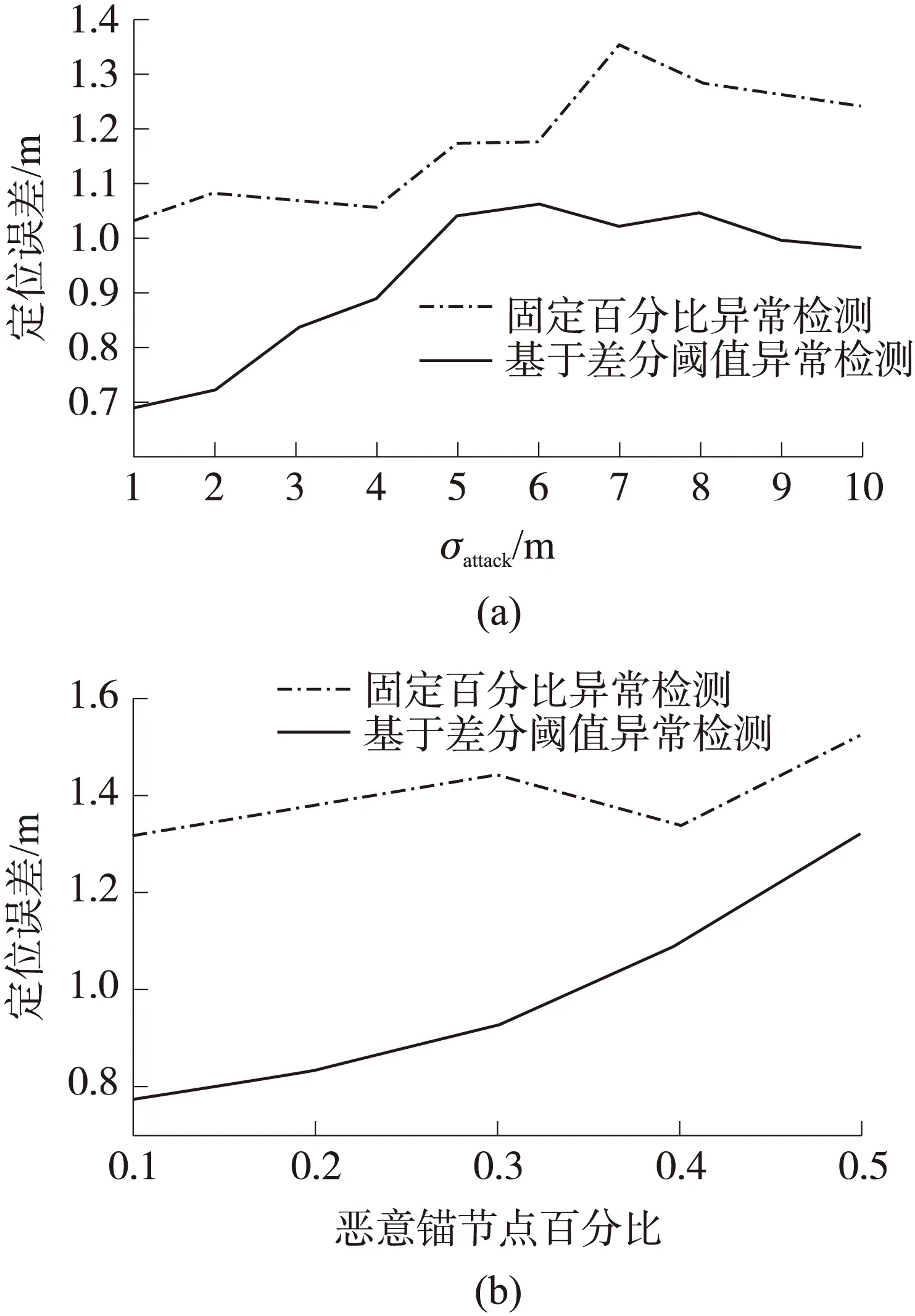
图6 基于差分阈值和固定百分比异常检测比较图

4 结束语

本文提出了一种基于牛顿迭代法的无线传感器网络安全定位算法。该算法在定位精度、收敛次数和稳定性方面都要优于梯度下降法。同时,本文还对异常检测阶段作了分析及改进,针对异常检测过滤固定百分比锚节点的不足,提出了可以自适应调整过滤锚节点数目的基于差分阀值的安全检测法,从而进一步提高算法的定位精度。

[1] Kuriakose J,Joshi S,Raju R V,et al. A Review on Localization in Wireless Sensor Networks[M]//Advances in Signal Processing and Intelligent Recognition Systems. Springer International Publishing,2014:599-610.

[2] Demigha O,Hidouci W K,Ahmed T. On Energy Efficiency in Collaborative Target Tracking in Wireless Sensor Network:A Review[J]. Communications Surveys and Tutorials,IEEE,2013,15(3):1210-1222.

[3] 孙启永,张文,李海波,等. 基于微电极阵列和无线传感器网络的水环境重金属检测系统研究[J]. 传感技术学报,2013,26(7):907-911.

[4] Chen C C,Chang C Y,Li Y N. Range-Free Localization Scheme in Wireless Sensor Networks Based on Bilateration[J]. International Journal of Distributed Sensor Networks,2013,2013.

[5] Cheng L,Wu C,Zhang Y,et al. A Survey of Localization in Wireless Sensor Network[J]. International Journal of Distributed Sensor Networks,2012,2012.

[6] Vaghefi R M,Schloemann J,Buehrer R M. NLOS Mitigation in TOA-Based Localization Using Semidefinite Programming[C]//2013 10th Workshop on Positioning Navigation and Communication(WPNC). IEEE,2013:1-6.

[7] Lin L,So H C,Chan F K W,et al. A New Constrained Weighted Least Squares Algorithm for TDOA-Based Localization[J]. Signal Processing,2013,93(11):2872-2878.

[8] Livinsa Z M,Jayashri S. Performance Analysis of Diverse Environment Based on RSSI Localization Algorithms in WSNS[C]//2013 IEEE Conference on Information and Communication Technologies(ICT). IEEE,2013:572-576.

[9] 叶阿勇,许力,林晖. 基于RSSI的传感器网络节点安全定位机制[J]. 通信学报,2012,33(7):135-150.

[10] Chen H,Lou W,Wang Z. A Novel Secure Localization Approach in Wireless Sensor Networks[J]. EURASIP Journal on Wireless Communications and Networking,2010,2010:1-12.

[11] 陈宜,蒋朝惠,郭春. 一种抗独立攻击的WSN三维安全定位算法[J]. 传感技术学报,2015,28(11):1702-1707.

[12] Yu N,Zhang L,Ren Y. BRS-Based Robust Secure Localization Algorithm for Wireless Sensor Networks[J]. International Journal of Distributed Sensor Networks,2013,2013.

[13] Li Z,Trappe W,Zhang Y,et al. Robust Statistical Methods for Securing Wireless Localization in Sensor Networks[C]//Proceedings of the 4th International Symposium on Information Processing in Sensor Networks. IEEE Press,2005:12.

[14] Garg R,Varna A L,Wu M. An Efficient Gradient Descent Approach to Secure Localization in Resource Constrained Wireless Sensor Networks[J]. IEEE Transactions on Information Forensics and Security,2012,7(2):717-730.

[15] Garg R,Varna A L,Wu M. Gradient Descent Approach for Secure Localization in Resource Constrained Wireless Sensor Networks[C]//2010 IEEE International Conference on Acoustics,Speech and Signal Processing. IEEE,2010:1854-1857.

滕 云(1992-),男,湖南常德人,湖南大学硕士研究生,研究方向为无线传感网络定位和安全,1090317073@qq.com;

刘宏立(1963-),男,湖南常德人,湖南大学教授,博士生导师,研究方向为无线传感网络、移动通信系统与软件无线电、智能信息处理与传输技术,hongliliu@hnu.edu.cn。

A Secure Localization Algorithm Based on Iterative Optimization Method*

TENG Yun,LIU Hongli*
(College of Electrical and Information Engineering,Hunan University,Changsha 410082,China)

Because wireless sensor network nodes are often deployed in malicious environment,the node cannot get accurate location information,which leads to the destruction of network security. For the problem of secure location of wireless sensor networks in malicious environment,a new security localization algorithm based on Newton iteration method is proposed. Firstly,the security localization model is established,then the gradient vector is analyzed in the process of iteration,and the anomaly detection process is improved and optimized by using the differential threshold method. Finally,the unknown node is realized high-precision positioning result by residual information of anchor node and Newton iteration method,and further improving the node positioning accuracy. The simulation results show that Newton iterative method is better than gradient descent method in location application,and the optimized security location algorithm has better location accuracy and robustness.

wireless sensor network;secure localization;Newton iteration method;anomaly detection;differential threshold algorithm

项目来源:中央国有资本经营预算项目(财企[2013]470号);中央高校基本科研项目(2014-004);国家自然科学基金项目(61172089);湖南省科技计划项目(2014WK3001);中国博士后科研基金项目(2014M562100);湖南省科技计划重点项目(2015JC3053)

2016-07-04 修改日期:2016-12-16

TN212.9

A

1004-1699(2017)04-0570-05

C:7230

10.3969/j.issn.1004-1699.2017.04.015