WSN中DV-Hop节点定位算法的改进

任克强,李亚杰(江西理工大学信息工程学院,江西 赣州 341000)



WSN中DV-Hop节点定位算法的改进

任克强*,李亚杰
(江西理工大学信息工程学院,江西 赣州 341000)

为降低传统DV-Hop算法对未知节点估算距离的误差,提升WSN中的未知节点定位精度,提出一种基于未知节点估算距离修正的DV-Hop改进算法。该改进算法首先对节点的平均每跳距离进行修正,并根据节点分布和节点间邻居关系的特点引入节点远离度的概念,以区分未知节点和邻居锚节点的距离,降低估算距离的误差;然后对最小二乘法的误差进行修正,并利用邻居节点的通信范围限制关系对未知节点估算坐标的误差进行修正,以进一步减小未知节点的定位误差。实验结果表明,与传统DV-Hop算法及相关文献相比,改进算法可以有效减小未知节点估算距离的误差,提升未知节点定位的精度。

无线传感器网络;节点定位;DV-Hop算法;估算距离;误差修正

在无线传感器网络WSN(Wireless Sensor Network)中,许多应用都依赖传感器的自我定位,如海水监测、交通控制、地质勘测、抗震救灾等,这取决于准确获取传感器节点的位置信息[1]。获取WSN中节点位置坐标的算法依据是否需要测量节点之间的相互距离可分类成基于测距和无需测距的定位算法[2];在低成本和低能耗等要求约束下,后者不依赖特殊硬件,相比于前者更具有优势[3]。

DV-Hop定位算法是一种广泛应用的无需测距定位算法,但当WSN中传感器节点分布不均匀和不规则时,DV-Hop算法存在定位误差较大的缺陷[4]。为了使定位的结果更加准确,相关研究者分别对其进行了不同程度的改进。文献[5]通过引入距离矫正因子的概念以修正未知节点到锚节点的距离,使其更接近实际值,达到了减小定位误差的目的。文献[6]根据跳数阈值选择合理的平均跳距来估计距离,同时利用质心算法和最小二乘法综合估计定位坐标,有效改善了定位精度。文献[7]采用多个节点通信半径值进行多次节点信息广播,精确了未知节点到锚节点的跳数信息,降低了定位误差,但增加了节点间通信的开销。文献[8]将网络中全部锚节点平均跳距最大值与最小值的平均值作为全网平均跳距,最后通过细菌觅食算法(BFO)来定位未知节点,有效地提高了传感器节点分布不规则时的定位精度。文献[9]通过距离三角不等式来约束多跳距离误差,并采用加权双曲线法来代替最小二乘法计算坐标,在一定程度上提升了定位准确度,但使用了额外的硬件设施。文献[10]使用RSSI测距模型并对传感器节点进行限跳处理,然后对锚节点优化组合,最后采用质心估算法定位未知节点坐标,在减小定位误差的同时有效地减小了节点间通信信息量,但限跳会导致一些待定位节点因不能与锚节点通信而无法得到其位置坐标。文献[11]通过对误差距离加权与修正,选择合理的跳段距离并使用遗传算法计算未知节点位置,使定位结果更加准确。文献[12]提出一种新的平均跳距求解方法,首先未知节点获取所有邻居锚节点的平均跳距,通过该跳距求出邻居锚节点间相互距离并与实际值比较,引入百分比误差作为加权系数的参考依据来计算未知节点的平均跳距,提高了定位性能。

针对传统DV-Hop算法在随机网络中表现出的局限性,本文对其不合理的方面进行了分析研究和改进,提出一种基于未知节点估算距离修正的改进算法,使得节点间估算距离更接近实际值,以提升传统DV-Hop算法的定位精度。

1 DV-Hop算法

DV-Hop算法主要包括以下3个步骤[13]:

①计算节点间最小跳数

相邻节点间互相交换信息,使得网络中所有节点均取得每个锚节点的坐标和与其间的最小跳数。

②计算节点间跳段距离

(1)

(2)

式中:Hopsizei为锚节点i的平均每跳距离,dij和hij分别为锚节点i、j之间的距离值和跳数,(xi,yi)和(xj,yj)分别为锚节点i、j的位置坐标。

锚节点将计算出的平均每跳距离作为校正值向网络广播,每一个未知节点只保留最先获得的校正值,最后将校正值和到其他锚节点的跳数相乘得到该未知节点到其他锚节点的跳段距离。未知节点k和锚节点j之间的跳段距离dkj:

dkj=Hopsizei×hkj

(3)

式中:Hopsizei为k最先保留的校正值,hkj为k、j间的跳数。

③计算未知节点坐标

当待定位节点通过式(3)取得不少于3个跳段距离值时,其位置坐标可以通过极大似然估计法来求解。

如果待估算节点位置坐标为(x,y),到锚节点i的估计距离为di,(i=1,2,…,n),i的位置坐标为(xi,yi),(i=1,2,…,n),可得到方程组:

(4)

将式(4)中前(n-1)个等式分别与第n个等式相减可以得到AX=b形式的线性方程组,其中:

(5)

(6)

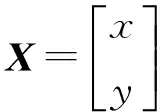
(7)

由最小二乘法,解得:

X=(ATA)-1ATb

(8)

2 DV-Hop算法分析与改进

DV-Hop算法定位过程中,未知节点与锚节点的距离并不是实际环境中两点之间的距离,而是采用平均每跳距离与跳数相乘求出的跳段距离来估计的,平均每跳距离是根据锚节点的分布情况计算出的,因而导致在WSN节点分布不均匀和不规则时,必然存在较大的定位误差。因此,本文从平均每跳距离、未知节点和锚节点的估算距离、最小二乘法引起的误差以及未知节点定位坐标值误差4个方面对DV-Hop算法进行了分析和修正改进。

图1 节点通信示意图

2.1 平均每跳距离的修正

根据DV-Hop算法原理可知,为使得节点间跳数最小,节点在与相距较远的节点通信时,会途经靠近通信范围边沿的节点。例如在图1中,A、B、C和D分别为WSN中的4个传感器节点,B、C均在A的最大通信半径范围内,为使得A与D之间通信时的跳数最小,A与D通信时则会途经更靠近通信范围边沿的C,而不经过B。

对于传感器节点均匀分布的WSN环境,节点的一跳距离长度更接近于通信半径的大小,由式⑴可知,平均跳距是由锚节点间实际距离总和除以其间跳数总和得出的,实际环境中节点随机分布,若锚节点间相距过近,如图1中节点A和B,则平均每跳距离值的计算误差会偏大,进而影响定位效果。为减少因锚节点相距过近而引起的误差,对由式⑵计算的dij进行以下修正:

(9)

2.2 未知节点到锚节点距离的修正

在DV-Hop算法定位过程中,待定位节点与各个锚节点的估计距离是采取同一个平均跳距值乘以对应的跳数得出的结果,这样会造成一定的误差[14]。在图1中,设节点B、C、D是锚节点,A是待定位节点,则A到B、C都是一跳,则根据式(3)计算出的A分别到B、C的距离是相等的,但实际上是不相等的,若按照相等的距离进行定位计算,显然是不合理的,导致定位结果不准确。另一方面,假定A的平均跳距值是从B获得的,大小为HopsizeB,若此值存在较大误差,则A到其他锚节点的估算距离值的误差会随着跳数的增加而被累积,且HopsizeB无法代表整个网络的分布情况;例如在图1中,在估算A与D的距离时采用HopsizeB,显然忽视了D周围的分布情况。

①未知节点与邻居锚节点距离的修正

为了区分不同未知节点与同一个邻居锚节点的估计距离,本文引入节点远离度的概念,用来表征未知节点与邻居锚节点相离远近的程度:

(10)

式中:εik为未知节点k与其邻居锚节点i的远离度,其值的大小和k、i间的距离正相关;Seti和Setk分别为i和k的邻居节点标号集合,crad(Seti∪Setk)为Seti、Setk并集中所有元素个数,crad(Seti∩Setk)为Seti、Setk交集中所有元素个数。

下面用图2举例,说明节点远离度的计算过程。A为锚节点;B、C分别为节点A单跳范围内的未知节点;粗实线大圆、细实线大圆和虚线大圆分别为节点A、B和C的单跳通信范围;空心小圆圈为其它传感器节点。A和B的邻居节点标号集合分别为SetA和SetB。可以算出,crad(SetA∪SetB)为21,crad(SetA∩SetB)为7,B与A的远离度εAB=21/7=3,C与A的远离度εAC=17/12≈1.42。远离度εAB>εAC说明B和A相离更远,两者的距离更接近通信半径,C和A相离更近。

图2 远离度计算说明图

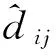
(11)

式中:εik为k与i的远离度,εimax为i所有邻居节点与i的远离度最大值。

②未知节点与非邻居锚节点距离的修正

(12)

式中:Hopsizei为k在DV-Hop算法第2)步获取的校正值,Hopsizej为j的平均跳距,hkj为k到j的跳数。

2.3 最小二乘法误差的修正

在利用最小二乘法求解过程中,将式(4)中前(n-1)个等式分别与第n个等式相减可得出式(6),从而式(6)中每一项均包含dn,若dn的值误差偏大,则必然给最后的定位结果带来一定的误差[15]。考虑到此过程中存在的问题,本文将式(4)中的n个等式重新按d1,d2,…,dn的值从大到小降序排列,使得第n个等式中dn的值最小,进而降低式(6)中向量b的误差,然后按式⑻求解得出定位坐标。

为了便于分析比较,本文将通过以上改进后的DV-Hop算法称为本文算法1。

2.4 未知节点坐标值误差的修正

未知节点由本文算法1计算得出的坐标X′与实际坐标X相比仍然存在一定误差,此误差体现在未知节点和锚节点的距离上,例如X′与X分别和每个锚节点相距远近程度是有差异的。为简化计算量,只考虑跳数是否为1的差异,即节点是否为邻居关系的差异,实际中节点应满足要求:对于具有邻居关系的两个节点,节点间距离不超过通信半径,相反,对于不具有邻居关系的两个节点,节点间距离大于通信半径[16],所以对X′为满足实际情况进行修正。

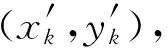
(13)

(14)

(15)

式中:(xj,yj)(j=1,2,…,n)为锚节点坐标,Lx和Ly分别为网络区域横坐标和纵坐标的最大值,对式⒂求解得到最后的修正位置坐标,称为本文算法2。

未知节点k误差修正的流程如图3所示。

下面以图4为例,说明未知节点k误差的修正过程。图中节点1、2、3和4均代表参与k定位计算的锚节点,空心小圆代表k的真实位置,空心三角为本文算法1定位得出的估算位置,用k1表示,由式(13)可得,Dk=(-1,-1,1,1),-1表示k1和锚节点1、2不为邻居关系,1表示k1和锚节点3、4为邻居关系。由式(14)可得,Hk=(-1,1,-1,1),表示k实际位置和锚节点1、3不为邻居关系,和锚节点2、4为邻居关系。Dk≠Hk表明估算位置k1不够准确,与实际位置存在误差,应使其为满足Hk所表示的关系进行修正,即与锚节点1保持非邻居关系不变,与锚节点4保持邻居关系不变,同时离开锚节点3使它们不为邻居关系,接近锚节点2使它们为邻居关系。满足条件修正距离最小的点为图中空心方框位置k2,即通过式(15)的计算会将k1位置坐标修正到k2位置,达到减小定位误差的目的。

图3 未知节点k坐标修正流程图

图4 未知节点k坐标修正举例

3 实验结果与分析

使用MATLABR2015b工具对DV-Hop算法、文献[11]算法、本文算法1和本文算法2进行实验仿真,并对实验结果进行对比和分析。实验仿真环境:在100m×100m的WSN环境中任意安放100个节点,包括锚节点和未知节点,且锚节点数量+未知节点数量=100,节点通信半径为R。

评价定位效果的标准为平均定位误差error和相对定位误差aerror:

(16)

aerror=error/R

(17)

图5是通信半径R=30m和R=35m时锚节点数目的变化对4种算法平均定位误差影响的实验结果。从结果可以看到,4种算法在锚节点数量依次递增且通信半径不变的情况下,平均定位误差都表现为递减变化,刚开始下降幅度较大,以后下降逐渐趋于缓慢。本文算法1平均定位误差在锚节点数量为5时和文献[11]算法接近,以后随着锚节点数量的增多均优于文献[11]算法;本文算法2是对本文算法1坐标误差修正的结果,从图5中可以看到达到了进一步减小误差的效果。图5(a)中锚节点数量为40时,本文算法2平均定位误差相比文献[11]算法和DV-Hop算法分别下降约2.7m和5.4m;通过图5(a)与图5(b)对比可以观察到,锚节点数量相同情况下,通信半径从30m变大为35m会使4种算法的平均定位误差都略有提升,原因在于通信半径增大使得锚节点平均跳距增大,进而使未知节点到锚节点的估计距离和实际值偏差变大,影响定位效果;但随着锚节点数量的增多,通信半径增大对本文两种算法的影响较小。

图5 不同锚节点数量的平均定位误差比较

图6是通信半径R=30m、R=35m和R=40m时锚节点数量的变化对4种算法相对定位误差影响的实验结果。从结果可以看到,在通信半径不变的情况下,4种算法的相对定位误差和图5变化趋势一致,都表现为先快速下降而后缓慢下降。在锚节点数量为5情况下本文算法1的相对定位误差与文献[11]算法差别比较小,以后随着锚节点数量递增均优于文献[11]算法和DV-Hop算法。图6(a)中本文算法2的定位性能相比文献[11]算法和DV-Hop算法分别提升5.0%～9.7%和12.8%～18.6%;由图6(a)、图6(b)和图6(c)对比可以看到,锚节点数量相同条件下,通信半径增大会使4种算法相对定位误差都表现出小幅度下降,这是因为通过式(17)计算平均相对误差时,通信半径在分母,使得计算结果偏小。

图6 不同锚节点数量的相对定位误差比较

图5和图6表明本文算法的定位性能优于文献[11]算法和DV-Hop算法,这是由于本文通过计算远离度对未知节点到锚节点的距离进行修正,并依据节点邻居关系对估算坐标值进一步修正,使其更接近实际值,相比于文献[11]算法和DV-Hop算法,本文算法的定位性能得到了有效提升。

图7是通信半径R=40m、锚节点数量n=25时DV-Hop算法和本文算法2的每个未知节点的定位误差。从图7中可以看到,两者定位误差差距较大,DV-Hop算法在11.5m左右波动,而本文算法2在4.5m左右波动,且有30.7%节点的定位误差在3m以内;因此,本文算法2不仅减小了定位误差,且稳定性也得到较好地提升。

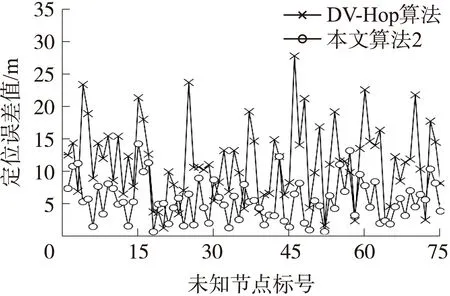
图7 未知节点的定位误差比较图

图8 未知节点的实际位置与定位位置比较

图8是R=50m、锚节点数量n=30时DV-Hop算法和本文算法2的每个未知节点的定位位置和实际位置,图中黑色小圆点表示实际坐标位置,空心小圆表示定位估计坐标位置,且图8(a)与图8(b)中黑色小圆点坐标位置相同。从图8(a)中可以看到,DV-Hop算法存在一部分节点的估计坐标位置超出了WSN节点部署区域范围的情况,这使得这些节点的估计坐标位置和实际位置距离相差过大,造成平均定位误差偏大的结果;而从图8(b)中可以看到,本文算法2不存在节点的定位位置超出WSN节点布署区域范围的情况,这是由于式(15)的约束作用,保证了所有节点的定位位置均在WSN节点部署区域范围内,而且相比DV-Hop算法显著提升了总体定位效果。

4 结束语

针对在随机分布网络环境中传统DV-Hop算法的局限性,对引起定位误差的来源进行研究和分析,提出一种改进的DV-Hop算法。改进算法从锚节点平均每跳距离的计算、未知节点到锚节点距离的计算、最小二乘法求解未知节点坐标以及坐标修正4个方面对传统DV-Hop算法进行了改进,并在不同锚节点数量和不同节点通信半径的WSN环境下进行了算法定位性能比较实验。实验结果表明,本文改进算法的平均定位误差和相对定位误差均优于传统DV-Hop算法及相关文献,有效提升了DV-Hop算法的节点定位性能。如何进一步减小未知节点定位位置与实际位置的误差是后续研究的重点工作。

[1] Xu C X,Chen J Y. Research on the Improved DV-Hop Localization Algorithm in WSN[J]. International Journal of Smart Home,2015,9(4):157-162.

[2] Safa H. A Novel Localization Algorithm for Large Scale Wireless Sensor Networks[J]. Computer Communications,2014,45(3):32-46.

[3] 曹欲晓,严奎,徐金宝. 一种最优锚节点集合上的两重粒子群优化DV-Hop定位算法[J]. 传感技术学报,2015,28(3):424-429.

[4] Fang X. Improved DV-Hop Positioning Algorithm Based on Compensation Coefficient[J]. Journal of Software Engineering,2015,9(3):650-657.

[5] Wu L,Hou Z,Tan C,et al. Improved DV-Hop Localization Algorithm Based on Distance Correction of Anchor Nodes[J]. International Journal of Future Generation Communication and Networking,2016,9(10):269-278.

[6] 向满天,王胜,杨友华. 基于阈值机制与距离校正的WSN改进DV-Hop定位算法[J]. 传感技术学报,2016,29(6):920-926.

[7] 刘士兴,黄俊杰,刘宏银,等. 基于多通信半径的加权DV-Hop定位算法[J]. 传感技术学报,2015,28(6):883-887.

[8] Zhao Q S,Hu Y L. An Improved DV-Hop Localisation Algorithm[J]. International Journal of Wireless and Mobile Computing,2016,10(1):20-25.

[9] 周玲,康志伟,何怡刚. 基于三角不等式的加权双曲线定位DV-Hop算法[J]. 电子测量与仪器学报,2013,27(5):389-395.

[10] 夏少波,邹建梅,朱晓丽,等. 基于跳数区域划分的DV-Hop改进算法[J]. 传感技术学报,2014,27(7):964-969.

[11] 程超,钱志鸿,付彩欣,等. 一种基于误差距离加权与跳段算法选择的遗传优化DV-Hop定位算法[J]. 电子与信息学报,2015,37(10):2418-2423.

[12] Wang Y,Fang Z,Chen L. A New Type of Weighted DV-Hop Algorithm Based on Correction Factor in WSNs[J]. Journal of Communications,2014,9(9):699-705.

[13] Zhang W,Yang X,Song Q. DV-Hop Localization Algorithm Based on RSSI Correction[J]. Journal of Software Engineering,2015,9(1):188-194.

[14] Zhang J,Guo N,Li J. An Improved DV-Hop Localization Algorithm Based on the Node Deployment in Wireless Sensor Networks[J]. International Journal of Smart Home,2015,9(10):197-204.

[15] 朱敏,刘昊霖,张志宏,等. 一种基于DV-Hop改进的无线传感器网络定位算法[J]. 四川大学学报(工程科学版),2012,44(1):93-98.

[16] Shang F,Lan L,Dong M. Position Location Scheme Using Nonlinear Programming Based on RSSI and DV-Hop[J]. International Journal of Hybrid Information Technology,2015,8(5):1-10.

任克强(1959-),男,教授,硕士研究生导师,主要研究方向为图像与视频处理、无线传感器网络、信息隐藏,jxrenkeqiang@163.com;

李亚杰(1992-),男,硕士研究生,主要研究方向为无线传感器网络。

Improvement of DV-Hop Node Localization Algorithm in WSN

REN Keqiang*,LI Yajie
(School of Information Engineering,Jiangxi University of Science and Technology,Ganzhou Jiangxi 341000,China)

In order to reduce the estimation error of the traditional DV-Hop algorithm,an improved DV-Hop algorithm based on modification of estimation distance was proposed to enhance the localization accuracy of unknown nodes in WSN. Firstly,the improved algorithm modified average distance per hop for nodes,and degree of distance among notes was introduced according to the nodes distribution and the characteristics of neighbor relation between nodes,so as to distinguish the distance between unknown nodes and anchor nodes,and to reduce the error of the estimation distance. Then,the error of the least squares method was modified,and the constraint relationships of communication range between neighbor nodes were utilized to modify the error of the estimation coordinates for unknown nodes,which could further reduce the error of locating unknown nodes. The experimental results show that compared with the traditional DV-Hop algorithm and the related reference,the improved algorithm can effectively reduce the error of the estimation distance for unknown nodes,and improve the localization accuracy of unknown nodes.

wireless sensor network;node localization;DV-Hop algorithm;estimation distance;error modification

2016-07-26 修改日期:2016-12-05

TP393

A

1004-1699(2017)04-0611-07

C:6150P

10.3969/j.issn.1004-1699.2017.04.022