垂线偏差对空中对准航向误差的影响研究*

夏家和,成果达,吉翠萍(西安飞行自动控制研究所,西安 710065)



垂线偏差对空中对准航向误差的影响研究*

夏家和*,成果达,吉翠萍
(西安飞行自动控制研究所,西安 710065)

针对性分析了垂线偏差变化对空中对准航向精度的影响。首先给出了常用空中对准降阶滤波模型,分析了垂线偏差变化影响空中对准航向误差的机理。然后通过实测离线数据测试验证了垂线偏差对空中对准航向误差的影响。最后通过误差协方差分析方法仿真了降阶滤波模型在真实世界中的滤波性能。离线测试及仿真结果表明:在给定条件下垂线偏差变化率对航向误差的影响相对其他未建模惯性测量组件误差是主要的,对航向对准误差影响较大,可达0.15°。在中高精度应用中为保证在不同空域内空中对准航向精度考虑采用高精度重力场模型对垂线偏差进行补偿是必要的。

捷联惯导;空中对准;协方差分析;垂线偏差

工程应用中重力加速度的补偿一般采用简化正常重力模型计算,忽略扰动重力。在中低精度惯导系统应用中,惯性测量组件误差是主要误差源,相对来说扰动重力对系统的影响可以忽略。随着惯性器件精度的不断提高及高精度惯性导航系统需求的发展,扰动重力已然成为高精度惯导一项不可忽略的误差源。重力扰动分为垂线偏差和重力值异常两部分,由于高度通道一般工作在阻尼状态,因此垂线偏差的影响大于单纯重力异常的影响。不少公开文献分析了垂线偏差对惯导系统的影响,包括地面罗经对准、导航及组合导航系统的影响[1-2]。文献[1]指出垂线偏差是高精度惯性导航系统的一项主要误差源,导出了初始对准阶段姿态的稳态误差值,对比了不同地区垂线偏差引起的导航误差。文献[2]通过对某海域重力异常的计算,分析扰动重力矢量引起的惯性导航系统位置与速度误差量级的大小及特性。但目前公开研究不涉及垂线偏差对动基座对准如空中卫星辅助对准的影响[3-6]。如文献[3]在进行空中对准误差分配分析时,提及重力模型误差,但没有深入对垂线偏差的影响进行分析。本文针对性分析垂线偏差对空中对准航向误差的影响,首先分析了垂线偏差影响空中对准航向误差的机理,然后通过实测数据离线对比了某次试飞试验数据补偿垂线偏差前后的航向对准精度,最后通过协方差分析方法分析了降阶空中对准算法在给定场景下的工作性能。分析结论对空中对准工程方案设计及简化有一定的借鉴意义。

1 空中对准算法

对于捷联惯导系统,导航坐标系选为东北天地理坐标系,降阶空中对准算法一般考虑其数学平台误差、速度误差、位置误差、陀螺随机常值漂移以及加速度计随机常值偏置,认为惯性测量组件的其他误差项及惯性系统与辅助卫星导航系统之间的时空差异已经得到很好的校正。空中对准的滤波状态向量x为:

x=[φT(δvn)Tδp(εb)T(b)T]Tδp=[δLδλδh]T

(1)

根据捷联惯导误差方程和器件误差参数模型,可列写出降阶空中对准的状态方程为[7]:

(2)

以惯性导航系统与卫星导航系统的速度、位置差作为量测量,量测方程为:y=[δvnδLδλδh]T=[06×3I6×606×6]x+v

(3)

v为量测噪声。式(2)和式(3)就组成了常用空中对准的降阶卡尔曼滤波模型。

2 垂线偏差影响

垂线偏差是由于地球地表形状不规则、地球内部质量分布不均匀等地理自然因素引起的实际重力方向与该位置点正常重力的小角度偏差。实际重力与正常重力的关系可表示为:

(4)

式中:δgn为重力扰动部分;η为卯酉面垂线偏差,绕北向轴为正;ξ为子午面垂线偏差,绕东向轴为正;式(2)中降阶空中对准滤波模型速度误差状态并未考虑重力模型误差影响,若考虑其影响相应的速度误差方程为:

(5)

重力水平分量对导航解算的影响一定程度上可等效为加计零位误差。地面静止对准时等效的加计零位不变,对对准精度的影响可参考文献[8-9]。垂线偏差随着载体位置(纬度、经度、高度)变化,空中对准时与地面对准不一样,载体位置变化较快,因此对准过程中垂线偏差在变化,会引对准过程中等效加计零位的变化,其中等效北向加计零位的线性变化影响航向对准精度。

图1 空中对准期间垂线偏差引起的水平重力分量

3 试验测试及仿真分析

通过离线实测数据对比测试及误差协方差仿真分析垂线偏差变化对空中对准航向误差的影响进行分析。

3.1 试验测试

为测试垂线偏差影响,选取某次咸阳-汉中航线试飞时垂线偏差变化较大区域的一段时间长度为600s的实测数据,数据包括原始400Hz惯性测量组件数据(角增量、速度增量)、卫星导航数据及其同步计数。试验用惯导系统位置精度0.8nm/h(CEP),陀螺漂移重复性0.007 °/h,加计零位重复性3×10-5gn。试验时载机飞行速度约220km/h,期间飞机基本处于平飞状态。在没有航线实测垂线偏差数据情况下,利用EGM2008(2 190阶)全球重力场模型进行重力向量计算。EGM2008地球重力场球谐模型是美国国家宇航局于2008年公布,将阶次完全至2 159(球谐模型的阶扩展至 2 190,次扩展至2 159),空间分辨率提高到了9km,在分辨率和精度方面都有了很大的提高[10-11]。采用EGM2008重力模型计算得到垂线偏差引起的重力水平分量如图 1所示。

由图1可知,重力北向分量在对准过程中基本呈线性变化,在600s时间变化约-1×10-4gn。以地面EIA对准后导航解算的航向作为参考,采用传统简化重力模型(即不考虑垂线偏差)和EGM2008模型(考虑垂线偏差)进行空中对准的航向误差比较如图2所示。

图2 垂线偏差补偿与否航向对准误差比较

由图2可知,不考垂线偏差比考虑垂线偏差航向对准误差大约0.15°。补偿垂线偏差后,系统航向对准误差在0.05°以内,可满足航空惯导位置误差漂移率1.5nm/h(CEP)的应用要求。垂线偏差补偿与否航向差约0.15度,相应数值与等效北向加计零位斜坡误差造成的航向误差相对应。

3.2 协方差仿真分析

误差协方差仿真分析是评估降阶卡尔曼滤波算法在真实环境下工作性能的有效方法[12]。协方差仿真提供了一种系统统计性能的仿真手段,通过协方差仿真可以避免通过大量的单次仿真进行统计而获得系统性能的预估。通过协方差仿真可以评估在特定任务场景下各项误差的贡献,据此可分析哪些误差在系统中是主要误差源,并且在后续系统实现中通过技术手段予以降低,以获得满足需求的导航系统性能[13]。

协方差分析时,采用正常重力模型对重力进行补偿。设计的15维降低滤波器如第2节所示。真实世界还包含重力模型误差(垂线偏差引起)及其他惯性测量组件误差状态。

为模拟3.1节测试场景,仿真时假定垂线偏差引起的重力东向、北向分量模型为:

(6)

这里针对重力北向分量的线性变化影响进行分析,式(6)中gE,gN,α对应初始方差阵的初值取为0,β对应的初始方差阵取为(-1.0×10-3/600)2。

具体真实世界的惯性测量组件误差状态仿真参数列于表1。由于对准时间短,惯性测量组件误差状态按随机常值建模。

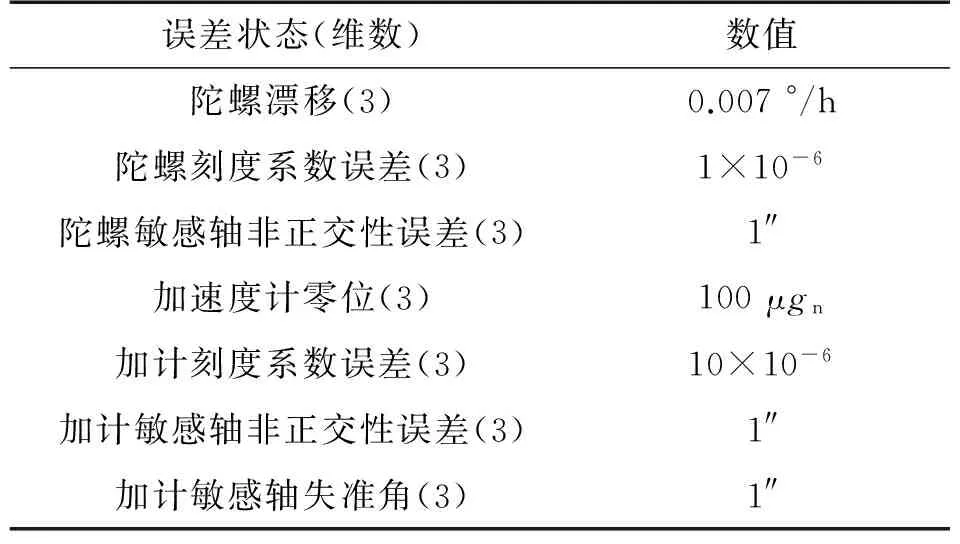
表1 真实世界惯性测量组件误差状态

真实世界在降阶模型的基础上增加仿真重力模型状态及表1所示的其他误差项,状态为34维。降阶空中对准滤波器的参数设置同真实世界。降阶空中对准滤波算法自身估计的航向误差(降阶滤波器协方差阵对应元素的根号值)和其在真实世界中工作的航向误差(协方差分析计算协方差阵对应元素的根号值)对比如图3所示。

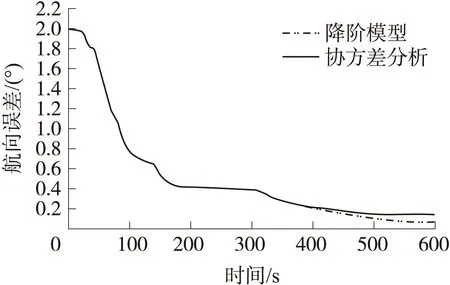
图3 降阶滤波器及真实协方差分析估计航向误差对比

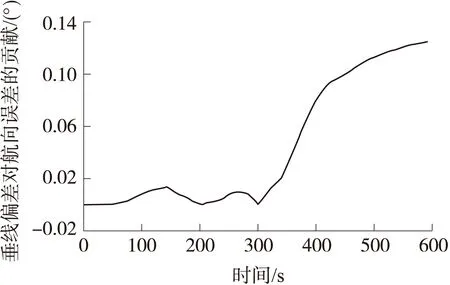
图4 垂线偏差引起的航向误差

由图3可知,由于滤波模型偏差降阶滤波器计算的方位角误差过小,对其工作性能的估计过于乐观,对比图2可知真实误差相对要大。相对的,降阶空中对准模型在真实世界的协方差分析结果可以较真实的反映滤波器工作性能。进一步的,单独协方差仿真了垂线偏差引起的航向误差,仿真结果如图4所示。

由图3、图4可知,垂线偏差对设定条件下空中对准航向误差影响是主要,而其他惯性测量组件误差是可忽略的。

4 结论

空中对准过程中垂线偏差变化的影响等效于加计零位变化,其中重力北向分量的线性变化将导致航向对准误差。实测离线数据测试结果显示采用EMG2008重力模型补偿垂线偏差后,在垂线偏差变化较大空域内的空中对准航向精度明显改善。误差协方差仿真分析进一步验证了在直飞情况下,垂线偏差变化率对航向误差的影响相对其他未建模惯性测量组件误差是主要的,对航向对准误差影响较大,制约后续纯惯性导航精度。因此在中高精度应用中为保证在不同空域内的空中对准精度考虑采用高精度重力场模型对垂线偏差进行补偿是必要的。

[1] 赵忠,王鹏. 高精度惯性导航系统垂线偏差影响与补偿[J]. 中国惯性技术学报,2013,21(6):701-705.

[2] 李姗姗,吴晓平,王凯. 扰动重力矢量对惯性导航系统的误差影响[J]. 大地测量与地球动力学,2010,30(3):142-146.

[3] 翁浚,秦永元,严恭敏,等. 空中对准方案的误差分配分析方法(英文)[J]. 中国惯性技术学报,2015,23(5):570-574.

[4] 朱长征,居永忠. 影响天文导航系统定位精度的两个因素分析[J]. 宇航学报,2010,31(10):2309-2313.

[5] 梅春波,秦永元,游金川. SINS基于非线性量测的大失准角初始对准算法[J]. 宇航学报,2016,37(3):291-297.

[6] 夏家和,秦永元,游金川. 摇摆状态下基于非线性误差模型的惯导对准研究[J]. 宇航学报,2010,31(2):410-415.

[7] 秦永元. 惯性导航[M]. 北京:科学出版社,2006.

[8] Britting K R,Palsson T. Self-Alignment Techniques for Strapdown Inertial Navigation Systems with Aircraft Application[J]. Journal of Aircraft,1970,7(4):302-307.

[9] 吴枫,秦永元,周琪,等. 基于重力矢量积分的SINS对准算法误差分析(英文)[J]. 传感技术学报,2013,26(3):361-366.

[10] 刘晓刚,吴晓平,赵东明,等. EGM96和EGM2008地球重力场模型计算弹道扰动引力的比较[J]. 大地测量与地球动力学,2009,29(05):62-67.

[11] Simon A Holmes,Nikolaos K Pavlis,Steve C Kenyon,et al. The Development and Evaluation of the Earth Gravitational Model 2008(EGM2008)[J]. Journal of Geophysical Research:Solid Earth(1978-2012),2012,117(B4).

[12] Paul G Savage. Strapdown Analytics[M]. Maple Plain,Minn:Strapdown Associates,2000.

[13] Jay Farrell. Aided Navigation:GPS with High Rate Sensors[M]. Electronic Engineering New York:McGraw-Hill,2008.

夏家和(1981-),男,博士,中航工业自控所高级工程师,研究方向为捷联惯导及组合导航,ftn2@163.com;

成果达(1988-),男,硕士,中航工业自控所工程师,研究方向为捷联惯导,dhcgdc@126.com。

Study on the Influence of the Deflections of the Vertical on the In-Flight Alignment Heading Error*

XIA Jiahe*,CHENG Guoda,JI Cuiping
(AVIC Xi’an Flight Automatic Control Research Institute,Xi’an 710065,China)

The influence of deflections of the vertical(DOV)on the in-flight alignment heading error is analyzed. Firstly,the reduced order in-flight alignment filtering model is presented,and the mechanism of the DOV influence on in-flight alignment heading error is analyzed. Then,comparative test are carried out by real off-line test data. Finally,the performance of the reduced order in-flight alignment filtering model is evaluated by error covariance analysis simulation. Off-line test and simulation results show that the heading error caused by DOV can reach 0.15°,which is main error source compared to other unmodeled IMU error under the given simulation condition. Employing a high-fidelity gravity field model to compensate the DOV error is necessary to ensure the in-flight alignment heading accuracy in different airspace.

strapdown inertial navigation;in-flight alignment;covariance analysis;DOV

项目来源:国家863高新技术计划项目(2015AA2060)

2016-10-9 修改日期:2016-11-22

U666.1

A

1004-1699(2017)04-0566-04

C:7630;7230

10.3969/j.issn.1004-1699.2017.04.014