删繁就简凸显本质，退回原点推导公式——以一道坐标系中旋转难题为例

☉浙江宁波市曙光中学 王海燕

删繁就简凸显本质，退回原点推导公式
——以一道坐标系中旋转难题为例

☉浙江宁波市曙光中学 王海燕

最近一次的中考复习模考卷中，我们选用了2016年河南省中考把关题，该题的最后一问有一定的难度，虽然也有少数学生解答出来，但是解法单一，且该解法对原题中的直角三角形有较大的依赖作用，备课组内几经讨论仍然没有生成较好的、更为自然的解法，后来大家求助网络，在某初中数学大群里开展研讨，得到不少有益的提示，使得我们对该题最后一问有了更为深入的认识，并且总结出坐标系中某一个点旋转前后对应点坐标之间的关系.本文梳理这次研讨，并针对命题与教学作出一些必要的反思.

一、写在前面

（1）求抛物线的解析式；

（2）当△BDP为等腰直角三角形时，求线段PD的长；

（3）如图2，将△BDP绕点B逆时针旋转，得到△BD′P′，且旋转角∠PBP′=∠OAC，当点P的对应点P′落在坐标轴上时，请直接写出点P的坐标.

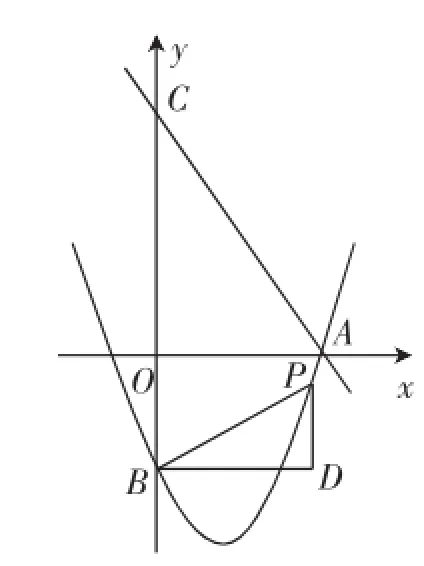
图1

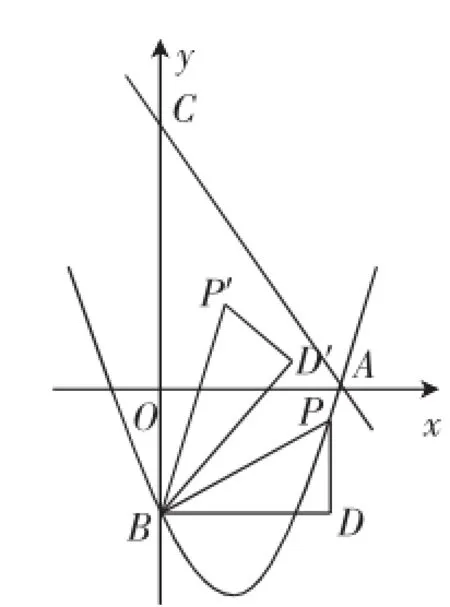
图2

思路解析：

（2）常规思考：要确定点P的位置（一般要进行分类），按点P在BD上方或下方，在y轴左侧或右侧可确定三种不同情况：①点P在y轴右侧且在BD上方；②点P在y轴右侧且在BD下方；③点P在y轴左侧.然后再有序解决问题：由△BDP是等腰直角三角形可知BD=PD，由点P′D′B的坐标分别表示出BD和PD的长，由BD=PD建立方程模型，从而求出m值，即得到PD的长.上面的思路可以看成是在黑暗中的摸索，当思路稍显明确之后，我们把上述思路简化表述：

简化思路：首先由△BDP为等腰直角三角形解读出PD=BD，设P用含参数m的式子表示PD、BD，得化为两个一元二次方程解得

另解突破：如果深刻认识到△BDP为等腰直角三角形，可直接读出直线BP的解析式为y=x-2或y=-x-2，把这两条直线的解析式分别与抛物线联立，得方程组

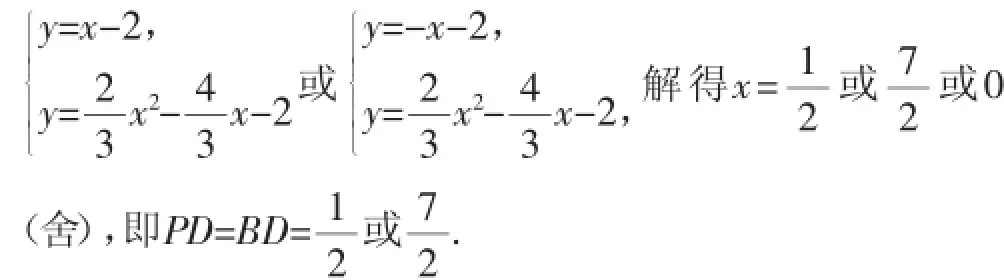
（3）常规思考：先分类思考点P的位置，可按点P在y轴左侧或右侧，旋转后点P′落在x轴或y轴,分为三种情况（如图3～5）：①点P在y轴左侧且点P′只能落在x轴上；②点P在y轴右侧且点P′落在x轴上；③点P在y轴右侧且点P′落在y轴上.接着尝试构造相似或全等的直角三角形，利用相似或三角函数建立方程突破.具体解析如下：

图3

先解读两个特殊角的三角函数值.由OA=3，OC=4，得AC=5.又∠PBP′=∠OAC，则sin∠PBP′=另外，还要记住在上一问中我们就已得出的PD=

①如图3，当点P′落在x轴上时，过点D′作D′N⊥x轴于N，交BD于点M，∠DBD′=∠ND′P′=∠PBP′，ND′-MD′，注意后者对应的图形是图4.

图4

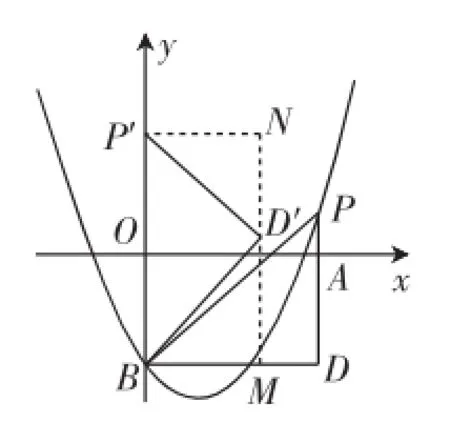
图5

②如图5，当点P′落在y轴上时，过点D′作D′M⊥x轴交BD于点M，过点P′作P′N⊥y轴，交MD′的延长线于点N，∠DBD′=∠ND′P′=∠PBP′，P′N=BM，即

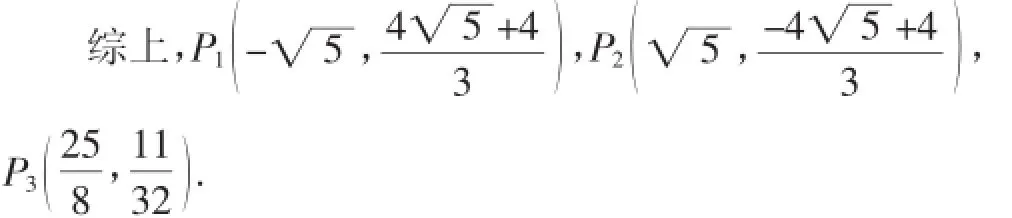
解后反思：上述解法过分依赖△BPD，而问题的本质却只是线段BP绕点B旋转后的探究.可简化如图6所示

删繁就简，简化问题：在平面直角坐标系xOy中，点P是抛物线动点，该抛物线与y轴交于点B（0，-2），将线段BP绕点B逆时针旋转α角后，得到线段BP′，若tanα=当点P′落在坐标轴上时，求点P的坐标.

简化思考，发现性质：如图7，在平面直角坐标系xOy中，若将P（x，y）绕坐标原点逆时针旋转θ角得到点P′（x′，y′）.

图7

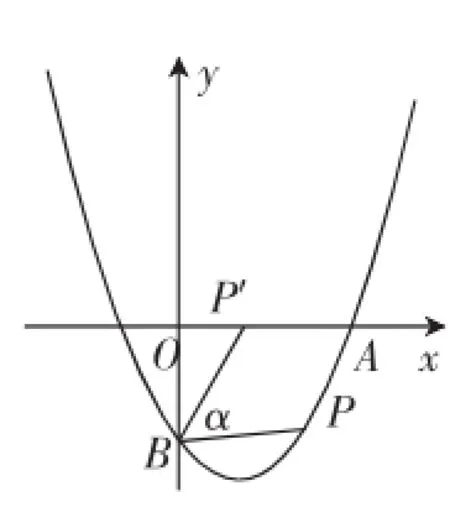
图6

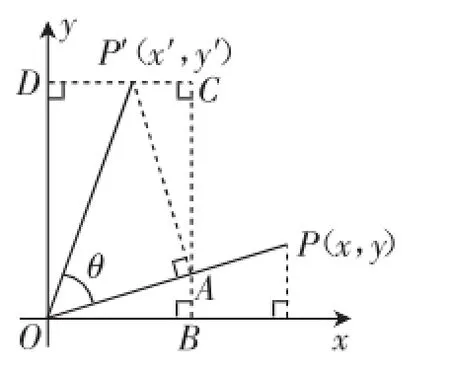
图8

在图8中，构造矩形OBCD，设OP=OP′=r，则：

成果扩大，归纳性质：我们可延续上述方法，推导并总结出平面直角坐标系中点的旋转公式如下：任意点A（x，y）按旋转中心（a，b）逆时针旋转θ角得到点A′（x′，y′），则A′（x′，y′）的坐标计算公式为：

x′=（x-a）·cosθ-（y-b）·sinθ+a，y′=（x-a）·sinθ+（y-b）· cosθ+b.

二、关于命题和解题教学的相关思考

1.命题时应该尽可能追求解法多样，满足不同学生的思维风格.

在我们研讨该题时，老师们多数认为第（3）问解法思路窄化，由常规思路不易切入，且对第（2）问中的直角三角形有一定的依赖，如果懂得及时删减无关线条的，反而会丢失必要的辅助工具（辅助直角三角形），使得问题的求解陷入僵局.而在考场上再去推导、演算出上面我们总结出来的旋转点坐标之间的规律或公式，则时间上往往并不能保证.我们认为，命题组在预设这类考题时，不能出于个性化的喜好，而以窄化的思路切入问题，对不同思维风格的学生要兼顾，也即命题人心中要时刻装着学生，时刻预设学生可能会怎样想，怎样想会更自然.

2.解题教学时要重视引导学生看清问题本质，传递“以退为进”策略.

解题教学时我们针对较为复杂的习题，常常要求学生懂得排除干扰，凸显问题本质，上面我们也是在这样的思考下开展的凸显本质图形（如图6）.然而根据图6，会失去原考题中那个直角三角形BPD的帮助，反而不利于构造处理.这时如果不能果断后退，退到图7，构造图8来辅助思考出旋转前后对应点的坐标关系式，则思路难以接通.所以，解题教学时，我们要向学生传递“以退为进”的策略，正所谓“解题要善于退，退到最简单的地方，再迎上去.”也想起那句著名的禅诗《插秧诗》，摘录如下，作为本文的结束：

手把青秧插满田，低头便见水中天.六根清净方为道，退步原来是向前.

1.王友峰.专业自主增设内容，回看陈题洞察结构—九年级“探究四点共圆”教学设计与解读［J］.中学数学（下），2016（12）.

2.付小飞.明辨并列与递进，引导分离和聚焦——2016年江苏苏州中考第28题解析与教学思考［J］.中学数学（下），2016（7）.

3.罗增儒.数学的领悟［M］.郑州：河南科学技术出版社，1997.

4.章建跃.“题型+技巧”的危害［J］.中小学数学（高中版），2010（11）.

5.郑毓信.多元表征与概念教学［J］.小学数学教育，2011（10）.