对一道期末考试题的研究与拓展

☉浙江绍兴市柯桥区平水镇中 沈岳夫

对一道期末考试题的研究与拓展

☉浙江绍兴市柯桥区平水镇中 沈岳夫

对试题的研究是教师在教学和复习中经常做的一件事，通过研究把蕴含其中的数学思想方法揭示出来，挖掘出隐含的问题的本质属性.不但可以提高学生的空间想象能力、逻辑思维能力、分析和解决问题的思维技能，优化数学思维品质，而且可以培养学生探索创新的能力.本文以嵊州市2016学年第一学期期末学业成绩调研测试八年级数学试题第26题（压轴题）为例，作一些探索.

一、试题呈现

题目：已知△ABC是等腰直角三角形，∠BAC=90°，AB=AC，点D是边BC上的一个动点（不运动至点B、C），点E在BC所在的直线上，连接AD、AE，且∠DAE=45°.

（1）若点E是线段BC上一点，如图1，作点D关于直线AE的对称点F，连接AF、CF、DF、EF.

①求证：△ABD≌△ACF；

②若BD=1，DE=2，求CE的长.

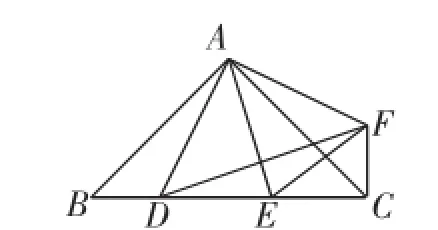
图1

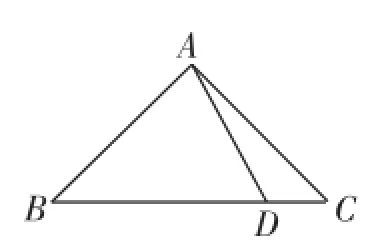
图2

此题以直角三角形为依托，全面考查全等三角形、轴对称图形及勾股定理等知识点，综合性较强.在中考复习时，笔者选择此题作为家庭作业，结果在批阅时大大出乎我的意料，发现第（2）题“卡壳”现象较严重，不少学生无从下手.那么该题如何解？有何规律？笔者愿以此文与各位同仁探讨.

【评析】这是一道典型的两边相等的大角夹其半角的试题，即两个图形中同一个顶点上的两个角有倍半关系，且倍角的两邻边相等.只要抓住变中不变的本质，就会使题目的证明迎刃而解.三个问题难度由浅入深，层层递进，学生的思维需要拾级而上，三个问题所表现的功能泾渭分明，清晰可见，问题之间确立的关系起承转合，水到渠成.第（1）题中的第①问谓“起”，问题的起源，起点低，容易上手，激发了学生进一步探究的信心；第②问谓“承”.承上启下，把第①问中的证明三角形全等过渡到计算线段长度，为第（2）题的设置作好铺垫；第（2）题谓“转”.峰回路转，问题考查的能力、基本思想和呈现方式都发生了很大变化，在求解时需积累感悟第（1）题的求解经验：先画出∠DAE=45°，作出对称图形，然后分类思考，即点E在点D的左侧与右侧的情形，这是破解第（2）题的关键.当然这些念头其实是由第（1）题迁移而来，是一种顺势而为，是一种经验的“喷薄”.

二、对第（2）题的研究与拓展

波利亚在《怎样解题》中指出“当我们的问题比较困难时，我们可能很有必要进一步把问题再分解成几部分，并研究其更细微的末节”.所以，研究几何图形，一个基本的方法就是认真分析条件，寻找与之相关的基本图形，并利用这个基本图形的暗示作用来获得或推理相关的结论.

就第（2）题而言，通过阅读题中条件，容易让我们想到熟悉的“半角”模型.何谓“半角”模型？如图3，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是BC、CD上的点，且∠EAF=，这样的图形我们叫“半角”模型.

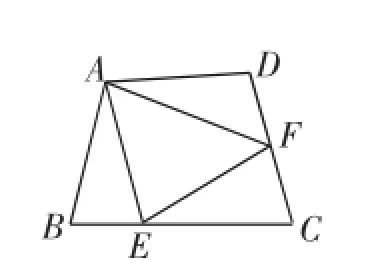
图3

“半角”模型是几何中的一个常见图形，因为“半角”模型便于迁移，并且结论异彩纷呈，涉及的解决问题的方法灵活多样，因此，它常常是各地命题者追逐的对象和日常教学研究的对象.

1.“半角”模型的特殊图形探究.

（1）如图4，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，求证：EF=BE+DF.

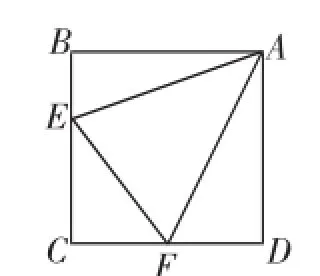
图4

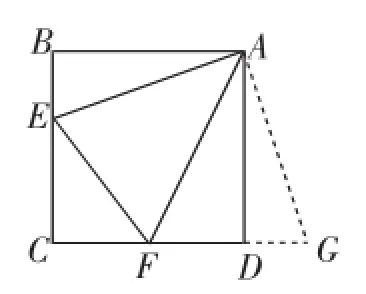
图5

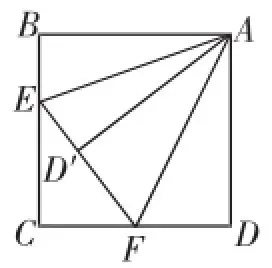
图6

简析：解决该问题的常规思路是截长补短法，如果我们从图形变化的角度来思考会更有数学的味道.思路1：如图5，把△ABE绕点A逆时针旋转90°得到△ADG，再证△AEF≌△AGF，进而求证.思路2：如图6，把△ADF沿AF对折，点D落在D′处，连接ED′，可证△ABE≌△AD′E，进而求证.以上给我们提供了解决“半角”模型的常用方法和思路.

（2）如果我们再连接对角线BD，交AE、AF于点M、N，如图7，求证：MN2=BM2+DN2.

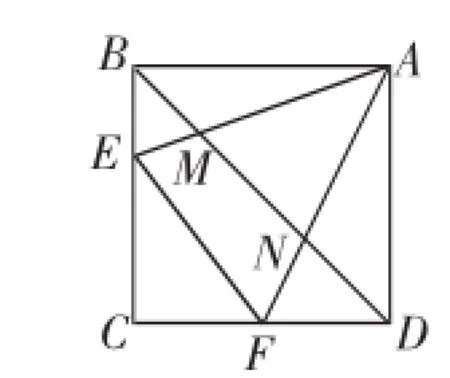
图7

图8

简析：如图8，把△ABM绕点A逆时针旋转90°到△ADM′，连接NM′，易证△ANM≌△ANM′，因为△NM′D为直角三角形，利用勾股定理进而求出关系，这里也可以选择轴对称思路来分析，此处不再赘述.

如果我们再把上述图形抽取变形，就可建立下面的基本模型：

（3）如图9，等腰直角三角形ABC中，∠BAC=90°，AB=AC，点M、N在边BC上，且∠MAN=45°，求BM、MN、NC之间的数量关系.

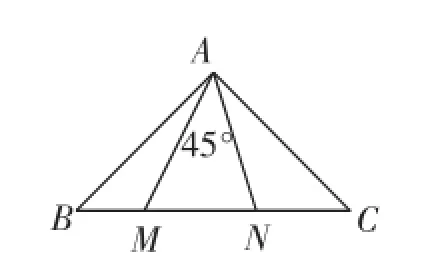
图9

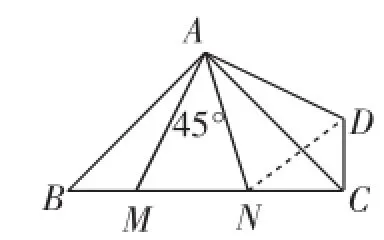
图10

简析：如图10，我们依然把△ABM把绕点A逆时针旋转90°得到△ACD，可以证得△AMN≌△ADN，把线段BM、MN、NC转化到了△DCN中.由于∠DCN=∠ACD+∠ACB=45°+45°=90°，所以由勾股定理，可得DN2=CD2+ CN2，即MN2=BM2+NC2.这样我们就得到了“半角”模型的又一个基本结论.

（4）如图11，等腰直角三角形ABC中，∠BAC=90°，AB= AC，点D在边BC上，点E在边BC的延长线上，且∠DAE= 45°，求DE、BD、CE之间的数量关系.

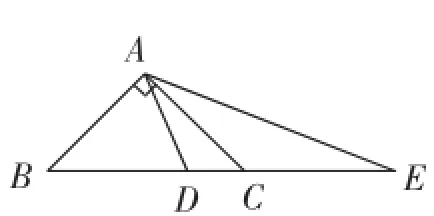
图11

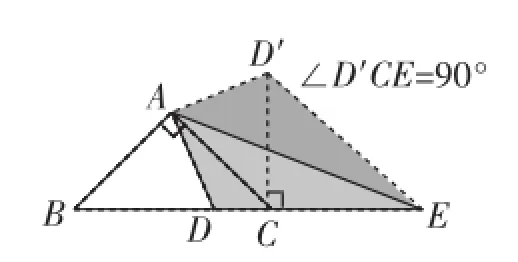
图12

简析：如图12，我们先把△ADE沿AE翻折得到△AD′E，易知△ADE≌△AD′E，从而可证△BAD≌△CAD′，进而知∠ACD′=45°，∠BCD′=90°，BD=CD′，所以把线段DE、BD、CE转化到了△CD′E中.由于∠D′CE= 90°，所以由勾股定理，可得D′E2=D′C2+CE2，即DE2=BD2+ CE2.这样我们就得到了“半角”模型的一个变式.

（5）如图13，等腰直角三角形ABC中，∠BAC=90°，AB=AC，点D在边BC的延长线上，且∠DAE=45°，EA的延长线交CB于点F.求DF、BD、CF之间的数量关系.

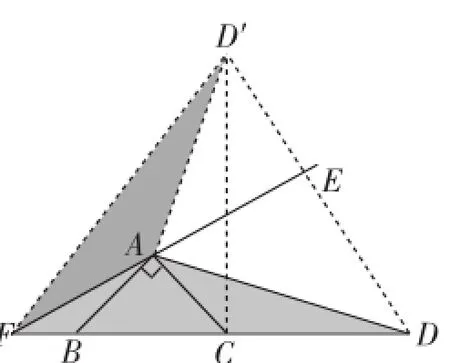
图14

图13

简析：如图14，我们先把△FAD沿AE翻折得到△FAD′，则FD=FD′.由题意可证△BAD≌△CAD′，进而知∠ACD′=45°，∠BCD′=90°，BD=CD′，所以把线段DF、BD、CF转化到了△CD′F中，由于∠D′CF=90°，所以由勾股定理，可得D′F2=D′C2+CF2，即DF2=BD2+CF2.这样我们就得到了“半角”模型的又一个变式.

上述问题是直角夹45°这一特殊的“半角”模型，我们由特殊延伸到一般，又会怎样呢？

2.“半角”模型的一般图形探究.

（6）如图15，等腰三角形ABC中，AB=AC，∠BAC=α，点M、N在边BC上，∠MAN=，BM=x，NC=y，MN=z，求x、 y、z的数量关系.

图15

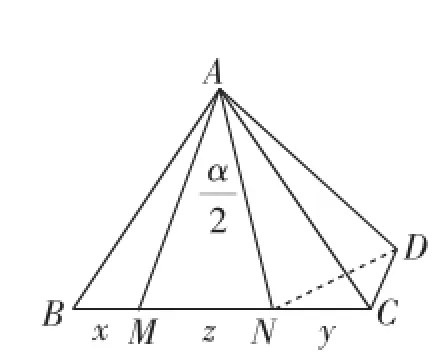
图16

在这里我们依然可以采用旋转变换的方式，如图16，把线段x、y、z转化到△DCN中，利用三角函数，可得到一般化的结论：z2=x2+y2+2xycosα（有兴趣的老师可以证一下，这里不再赘述），从而，α=90°其实就是“半角”模型的一种特殊情况，这也是问题的本质所在.

3.第（2）题的解题思路.

当点E在点D的左侧时，可仿照图9、图10的思路，求得CE=3；当点E在点D的右侧时，可仿照图11、图12的思路，求得所以CE=3或

4.“半角”模型的巩固提升题.

郑毓信教授曾说过：“知识求连，方法求变.”变则灵动，变则鲜活，变出智慧，变出情趣，“变”打开了学生获取解题方法的有效通道.进行有效试题“变式”可以链接不少中考试题，进一步感悟、理解问题的本质、数学思想方法，提升分析、思考、研究问题的思维能力.

1.（2011年咸宁市）（1）如图17，在正方形ABCD中，△AEF的顶点E、F分别在BC、CD边上，高AG与正方形的边长相等，求∠EAF的度数.

（2）如图18，在Rt△ABD中，∠BAD=90°，AB=AD，点M、N是BD边上的任意两点，且∠MAN=45°，将△ABM绕点A逆时针旋转90°至△ADH的位置，连接NH，试判断MN、ND、DH之间的数量关系，并说明理由.

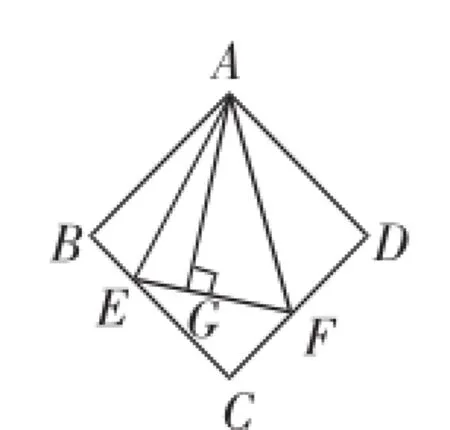
图17

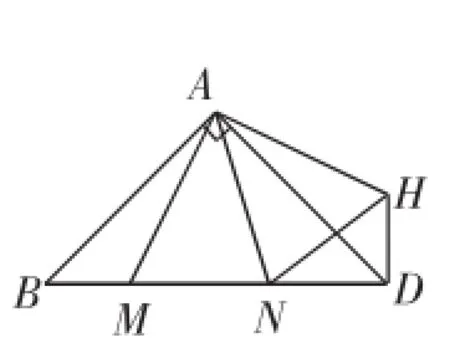
图18

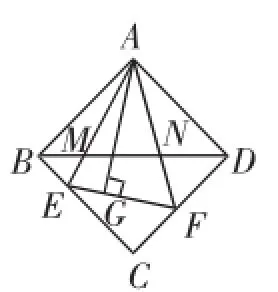
图19

（3）如图19，在图17中，连接BD分别交AE、AF于点M、N，若EG=4，GF=6，求AG、MN的长.

2.（2016年淄博市）如图20，正方形ABCD的对角线相交于点O，M、N分别是边BC、CD上的动点（不与点B、C、D重合），AM、AN分别交BD于点E、F，且∠MAN始终保持45°不变.

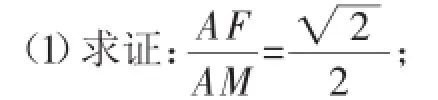
（2）求证：AF⊥FM；

（3）请探索：在∠MAN的旋转过程中，当∠BAM等于多少度时，∠FMN=∠BAM？写出你的探索结论，并加以证明.

图20

三、三点感悟

1.关注方法，为学生夯实知识保驾护航.

基本数学思想是贯穿数学问题的一条隐线，对解题起着高屋建瓴的指导作用.正如罗增儒教授认为的，题目的结论告诉我们向何方前进、预告需知，并引导解题方向.弄清了结论就等于弄清了行动目标，也就随身带了纠正偏差的指南针.上述题目的解法由结论的特殊形式能够想到勾股定理和直角三角形，这需要广泛的联想（即转化的前提）；再通过变换思想（翻折和旋转）将共线的三线段转化到一个三角形中，最终达到优化图形结构、整合图形信息的目的.这些都需要学生积极参与、独立思考、合作交流，才能逐步感悟.

2.立足模型，为学生能力提升铺路搭桥.

帮助学生积累数学活动经验是数学教学的重要目标，是提高学生数学素养的重要标志.此文所举的试题及相关问题题设中通常含有两边相等的大角夹其半角的特征，解法几乎都适用.因此，在平时的教学中，应紧紧抓住高效的中考题，努力挖掘试题的价值，不断引导学生对自己的解题过程进行反思、联想、总结，将高效的中考题发散，层层深入，化题为型，凝题成链，结题成网，让这类试题成为学生巩固知识、探究问题、发展能力、掌握思想方法的重要渠道，真正实现由“明一理”到“通一类”的飞跃，为学生的能力提升铺路搭桥.

3.问题领路，为学生思维升华拓展空间.

学起于思，教学活动的主线是解决问题.因此，教学过程应注重问题引导学生，围绕知识的核心，以数学知识再发现为线索，精心设置问题串，引导学生独立思考和探索，积累数学思维经验.笔者通过这些拾级而上、环环相扣的问题，在以方法、策略为主线，按由特殊到一般的顺序逐次展开的同时，激发学生的参与意识.同时，在循序渐进的设问和释问的过程中，使学生的思维逐渐驶入纵深处，使得课堂更加精彩.

1.叶纪元.解决一类中考题的利器：旋转、轴对称［J］.中学数学教学参考（中），2013（6）.

2.曹嘉兴.挖掘隐含结论提升解题能力［J］.中学数学（下），2013（2）.

3.沈岳夫.巧用45°特殊角妙解综合试题［J］.中国数学教育（初中版），2011（7/8）.

4.沈岳夫.对2014年浙江省绍兴市中考第23题的研究与拓展［J］.中国数学教育（初中版），2015（5）.