TMS:一种新的海量数据多维选择Top-k查询算法
刘显敏 李建中 高 宏
(哈尔滨工业大学计算机科学与技术学院 哈尔滨 150001) (xxhan1981@163.com)
TMS:一种新的海量数据多维选择Top-k查询算法
刘显敏 李建中 高 宏
(哈尔滨工业大学计算机科学与技术学院 哈尔滨 150001) (xxhan1981@163.com)
在许多应用中,Top-k是一种十分重要的查询类型,它在潜在的巨大数据空间中返回用户感兴趣的少量数据.Top-k查询通常具有指定的多维选择条件.分析发现:现有算法无法有效处理海量数据的多维选择Top-k查询.提出了一个基于有序列表的TMS(top-kwith multi-dimensional selection)算法,有效计算海量数据上的具有多维选择的Top-k结果.TMS算法利用层次化结构的选择属性网格对原数据表执行水平划分,每一个分片的元组以面向列的模式存储,并且度量属性的列表根据其属性值降序排列.给定多维选择条件,TMS算法利用选择属性网格确定相关网格单元,有效减少需要读取的元组数量,提出双排序方法执行多维选择的渐进评价,并提出有效剪切操作来剪切不满足多维选择条件和分数要求的候选元组.实验结果表明:TMS算法性能优于现有算法.
TMS算法;有序列表;选择属性网格;渐进选择评价;剪切操作
在许多应用中,Top-k是一种十分重要的查询类型,它在潜在的巨大数据空间中返回用户感兴趣的少量数据[1-2].通常,Top-k查询指定2个组件来反映用户的查询兴趣:评分函数F和多维选择P.根据定义的评分函数F,Top-k查询从满足P的数据空间中返回k个分数最大的元组.
由于在实际应用的重要性,Top-k查询已经获得研究人员的广泛关注[1].但是,现有的大多数工作都忽略了Top-k查询的多维选择,仅仅考虑有效计算全部元组的Top-k结果.当然,研究人员也提出了几种算法来处理多维选择Top-k查询.Bruno等人[3]将Top-kselection查询映射为范围查询,但是该方法实际上是计算多维空间上的k最近邻查询,不同于本文讨论的多维选择Top-k查询.Stupar等人[4]考虑处理基于集合选择的Top-k查询,即预先给定需要的元组ID集合,然后计算满足条件的查询结果.该方法的要求过于特殊,而且只考虑有一个度量属性的情况.Dong等人[5]提出ranking cube的方法来处理多维选择Top-k查询,该方法将data cube的思想和排序操作结合在一起来有效返回查询结果,但是该方法假设多维选择总是涉及到分类属性,并且在实际应用中构建和维护ranking cube的代价过于昂贵.综上所述,现有算法在海量数据上无法有效计算一般情况的多维选择Top-k查询.
本文提出一个新的基于有序列表的算法TMS(top-kwith multi-dimensional selection)来有效处理海量数据多维选择Top-k查询.该算法利用层次结构的选择属性网格对数据表进行水平划分,并且存储为面向列模式.TMS算法对度量属性对应的度量列表分片按照其属性值降序排列,保持选择属性对应的选择列表分片的原有顺序.给定多维选择,TMS算法根据网格结构快速确定相关的网格信息.在读取度量列表分片的元组时,本文提出双排序方法渐进地执行多维选择评价,从而减少了查询处理涉及到的IO费用.本文提出分数剪切操作和多维选择剪切操作,尽早丢弃那些不满足分数要求或者多维选择条件的候选元组.本文提出分数剪切的数学分析,来获得优化的剪切效果.本文的实验结果表明,和现有方法相比,TMS算法可以获得较大的性能优势.
本文的主要贡献有4点:
1) 提出一个新的基于有序列表的TMS算法,该算法利用选择属性网格来有效处理海量数据上多维选择Top-k查询;
2) 提出基于双排序的方法来有效执行渐进选择评价;
3) 提出有效的分数剪切和选择剪切操作,提出分数剪切操作的理论分析来获得优化剪切效果;
4) 实验结果表明:TMS算法与现有方法相比具有较大的性能优势.
1 预备知识
1.1 问题定义

多维选择Top-k查询:给定表T、多维选择P和评分函数F,多维选择Top-k查询在TP(T中满足P的元组集合)中返回一个k子集R,使得∀t1∈R,∀t2∈TP-R,F(t1)≥F(t2).
典型的多维选择Top-k查询SQL语句如下所示:
select * fromTwherel1≤S1≤u1andl2≤S2≤u2and… andld≤Sd≤udorder byw1×A1+w2×A2+…+wm×Amlimitk.
其中,lj和uj分别表示P在选择属性Sj指定的下界和上界.本文经常用到的符号如表1所示:

Table 1 The Symbol Notation
我们给出本文用到的位置索引的定义.
定义1. 给定表T,元组t∈T的位置索引是a,如果t是T的第a个元组.
我们用T(a)来表示表T中位置索引为a的元组,用T[a,…,b]表示位置索引大于等于a且小于等于b的元组集合,用T[a,…,b].Ai表示T[a,…,b]中元组的属性Ai的集合.
1.2 传统的有序列表Top-k查询算法
自从Fagin等人[6]的先驱性工作,利用有序列表来处理Top-k查询已经成为研究人员自然的选择[7-10].我们先介绍在不考虑多维选择情况下的有序列表Top-k查询算法.由于其较好的性能,本文采用LARA算法[7]为例来讨论有序列表Top-k算法.

由于LARA算法没有考虑多维选择的问题,下面我们提供2种方法来对其进行扩展.
1) 类树索引.一种直观的想法是以元组位置索引为键值在选择属性上构建类树索引.在LARA算法执行时,对于当前一轮获得的度量列文件ALi元组(pi,ai),根据类树索引和pi的值来判断元组T(pi)是否符合P,如果符合,那么对于该元组的处理类似于传统LARA算法,否则直接丢弃该元组,然后继续读取该列文件,直到获得一个满足条件的元组或文件遍历完毕.类树索引的问题在于,由于度量列文件ALi是根据属性值降序排列的,每次索引判断可能引起一个磁盘随机seek操作,在海量数据上执行时,这必然引起较多的大范围随机IO操作,严重影响算法的效率.因此,本文不再讨论这种方法.
下面我们扩展现有的LARA算法来处理多维选择.假设选择属性也存储为列文件形式,S1,S2,…,SD存储为选择列表集合{SL1,SL2,…,SLD},每个选择列表SLj(1≤j≤D)的模式为SLj(PI,Sj),其中Sj表示元组在对应选择属性的值,注意,这里的SLj的元组根据Sj的值升序排列,并在SLj.Sj上构建B+树.
2) 批量方法LBE(LARA with batch evalua-tion).该方法采用批量方法来处理多维选择.对读取度量列表之前,LBE算法先利用构建的B+树对SL1,SL2,…,SLd依次执行范围扫描操作,来获得满足多维选择的位向量B.∀t=T(pi),如果t满足P,那么位向量B的第pi位置为1,否则位向量B的第pi位置为0.接下来,LBE算法对度量列表执行元组读取操作,对于当前获得的ALi元组(pi,ai),LBE算法利用B的第pi位判断该元组是否符合P,如果满足条件则对该元组的处理类似于LARA算法,否则直接丢弃该元组,继续读取该度量列表,直到获得一个满足条件的元组.
2 有序列表Top-k算法的性能分析
为方便分析,我们假设表T的属性均匀独立分布.
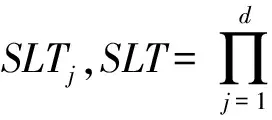
在海量数据上,表T维护大量元组,并且用户提交的查询通常只涉及一小部分元组,n的值较大而SLT的值较小.根据以上的描述,LBE算法存在3个问题:
1) LBE算法需要从SLj(1≤j≤d)中读取n×SLTj个元组;
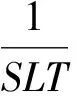
3) LBE算法需要维护一个n-bit的位向量,在海量数据上该位向量需要占据较多的内存空间.针对存在的问题,我们提出新的TMS算法有效处理海量数据多维选择Top-k查询.
3 TMS算法
3.1 算法概述
多维选择P实际给出一个查询子空间,如果在读取度量列表ALi(1≤i≤m)时,算法可以快速定位其对应行元组落入该子空间的元组,那么算法就可以较好地处理多维选择Top-k查询.本文采用选择属性网格来分布表T的元组,将对应网格的元组维护为列存储形式.基于选择属性网格的划分过程其实是把表T的Ai对应的度量列表ALi(1≤i≤m)划分为度量列表分片.给定多维选择条件P,算法可以根据网格结构来确定相关分片,也就确定了相关的度量属性列表分片.通常,与P相关的度量列表分片集合只是初始度量列表的一部分,从而有效减少读取不满足多维选择的元组的费用.本文还提出基于双排序的渐进多维选择评价方法来判断读取的度量属性是否符合P.为进一步减少双排序方法中需要评价的度量属性值的数量,本文提出有效的多维选择剪切操作和分数剪切操作.下面,我们分别介绍TMS算法的基本执行过程.
3.2 选择属性网格

图1给出的是D=2和MXH=2的SAL最底层划分情况,叶节点的编号表示其在兄弟节点中的次序.令TSAL(tncode)表示TSAL中编号tncode的节点.例如,具有编号“0100”的叶节点是编号“01”的节点的第1个孩子,而编号为“01”的节点是根结点的第2个孩子.
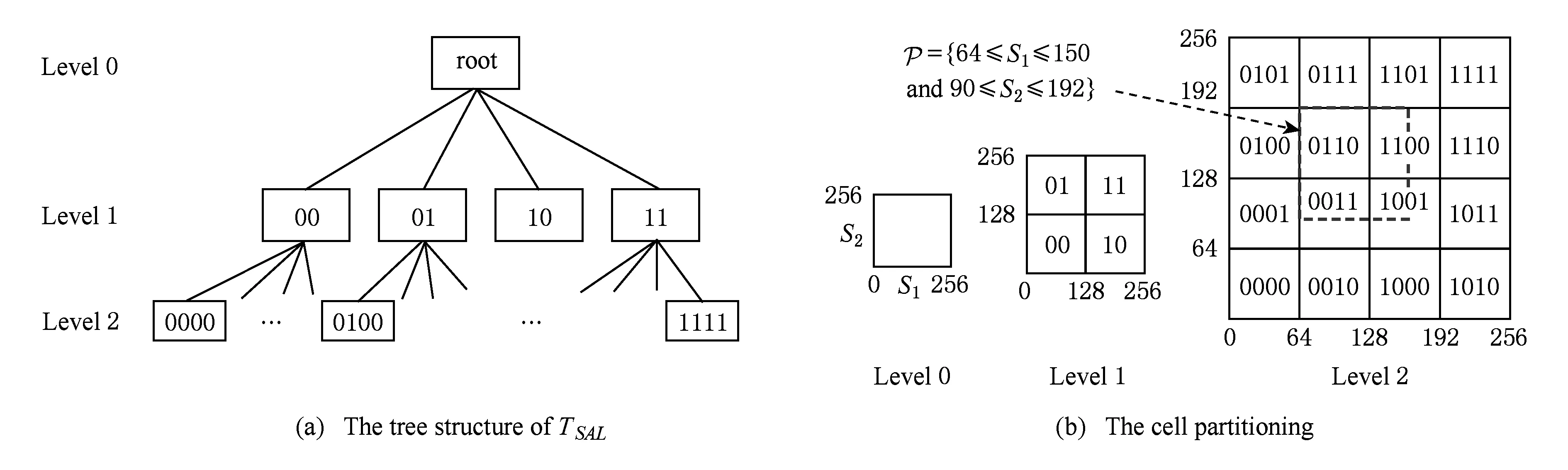
Fig. 1 The illustration of cell partitioning in SAL图1 选择属性网格底层划分
给定树结构TSAL,TMS算法顺序扫描表T,将表T的元组划分为(2D)MXH组分片,每一组分片维护着其选择属性落入对应子空间的元组集合.注意,TMS算法只将元组存储到TSAL的叶节点对应的分片,因此,TMS算法只维护表T的水平划分的单个副本.∀t∈T,TMS算法从根节点TNrt开始,根据元组t的选择属性值来决定该元组应当落入哪个子节点的子空间,令该元组落入根节点的第(b1b2…bD)2+1个子节点,其位bj(1≤j≤D)的取值如下定义:
该过程自TSAL的根节点开始执行,直到找到叶节点TNlf,元组t输出到TNlf对应的分片.对于每一个元组,TMS算法只需要进行MXH次判断就可以确定应当放入的分片.我们将叶节点对应的分片存储为面向列的格式,其中,度量列表分片和选择列表分片的模式分别为(PI,Ai,PIptn)和(PI,Sj).这里,PI表示对应元组在表T的位置索引,PIptn表示元组在对度量列表分片中的元组排序前的位置索引.
分片划分完毕后,TMS算法对每个叶节点对应的度量列表分片执行排序操作,使得度量列表分片的元组根据Ai降序排列,但对选择列表分片不排序.
3.3 查询处理
3.3.1 确定相关子空间
在执行查询处理时,TMS算法根据多维选择P来确定相关的子空间.对于P中任何未出现的选择属性Sj,我们通过在P中添加选择条件minSj≤Sj≤maxSj来扩展.这里,minSj和maxSj分别表示选择属性Sj的最小值和最大值.
给定多维选择P,TMS算法对TSAL执行层次遍历来确定不和P相离的叶节点.对于获得的叶节点TNlf,其处理方式如下:1)TNlf.hcube和P部分相交,TNlf插入到数组AP;2)TNlf.hcube被P包含,TNlf插入到数组AF.这里,AP维护其子空间和P部分相交的叶节点集合,AF维护其子空间被P包含的叶节点集合.
给定AP,令NAP表示AP的元素数量,TMS算法获得d个具有NAP个元素的数组PS1,PS2,…,PSd,其中,PSj(1≤j≤d)维护和Sj对应的相关选择列表分片,还获得m个具有NAP个元素的数组PR1,PR2,…,PRm,其中,PRi(1≤i≤m)维护和Ai对应的相关有序度量列表分片.
给定AF,令NAF表示AF的元素数量,TMS算法获得m个具有NAF个元素的数组FR1,FR2,…,FRm,其中,FRi(1≤i≤m)维护和Ai对应的相关有序度量列表分片.
3.3.2 多维选择评价
在执行过程中,TMS算法需要从PRi和FRi中按照降序顺序读取满足条件的度量属性Ai的值.在读取度量列表分片时,TMS算法渐进地计算当前读取的元组的多维选择评价结果.∀(pi,ai,piptn)∈PRi[h],T(pi).Sj的值出现在PSj[h](1≤j≤d)的第piptn个元组中,TMS算法需要读取PS1[h],PS2[h],…,PSd[h]的第piptn个元组来获得T(pi)的选择属性S1,S2,…,Sd的值,可以判断T(pi)是否满足P.如果对获得的每个来自PRi[h]的元组都根据其piptn的值来跳转到对应选择列表分片的指定位置进行多维选择评价,必然影响查询处理的效率.本文提出一个基于双排序的渐进评价方法,尽量采用磁盘顺序读取操作评价来自PRi的元组是否满足P.
双排序方法是:在每轮的元组读取操作中,TMS算法用大小为NAP的最大堆结构PMHi来读取PRi中当前最大的度量属性Ai的值,并且在内存中维护一个缓冲区PBi,令其大小为SZi.TMS算法分别读取PRi的每个分片的一个元组来填充PMHi,并不断读取PMHi的根节点元组来填充PBi.在填充PBi时,我们并不对来自PRi的元组执行多维选择评价,而是填充操作完成后批量地对PBi的元组执行多维选择评价.

假设PMHi的当前根节点元组t(PI,Ai,PIptn)∈PRi[h],将元组t填充到PBi时,执行t.PIptn+=OA[h].填充完毕后,TMS算法根据属性PIptn对PBi执行升序排序操作.根据定理1,排序后PBi中来自PRi[h]的元组连续存储,而这些元组对应的选择属性顺序存储在选择属性列表分片PSj[h](1≤j≤d).
定理1. 双排序方法的第1次排序后,PBi中来自PRi[h] (1≤h≤NAP)的元组连续存储,且这些元组对应的选择属性Sj(1≤j≤d)顺序存储在选择列表分片PSj[h].
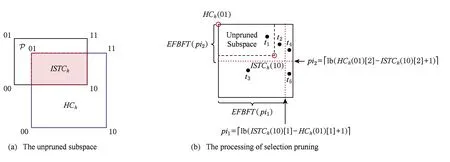
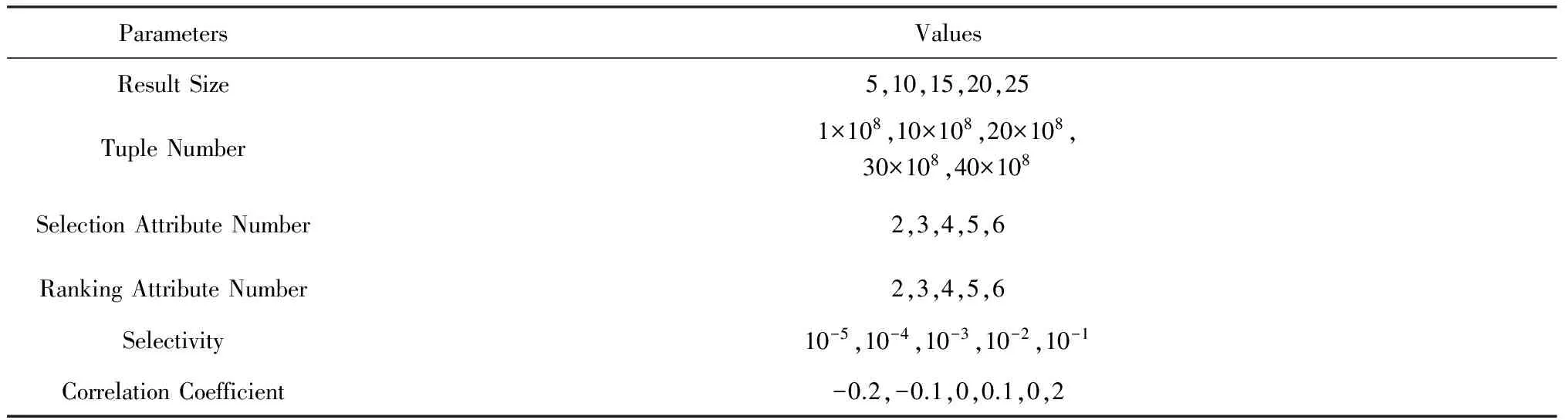
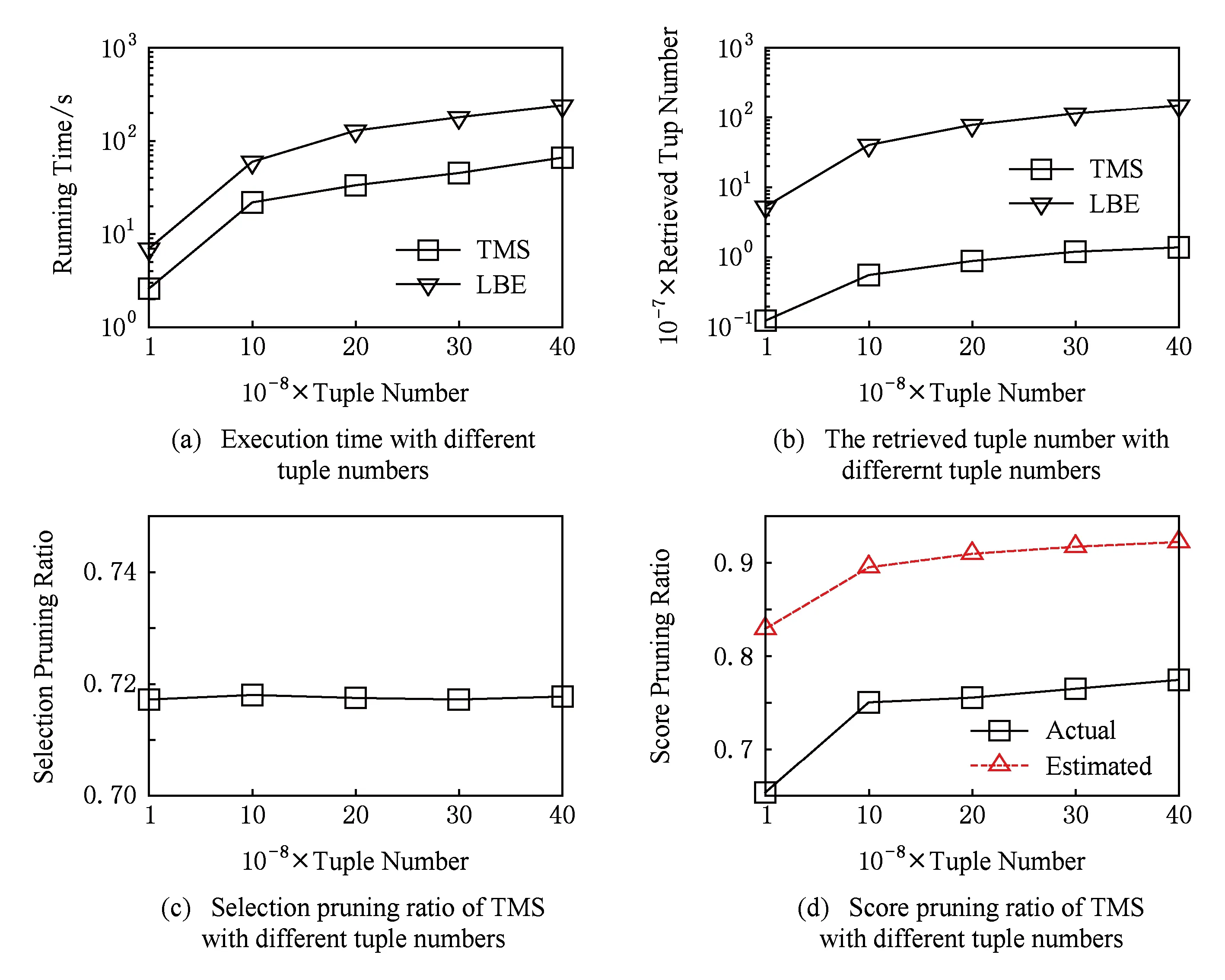
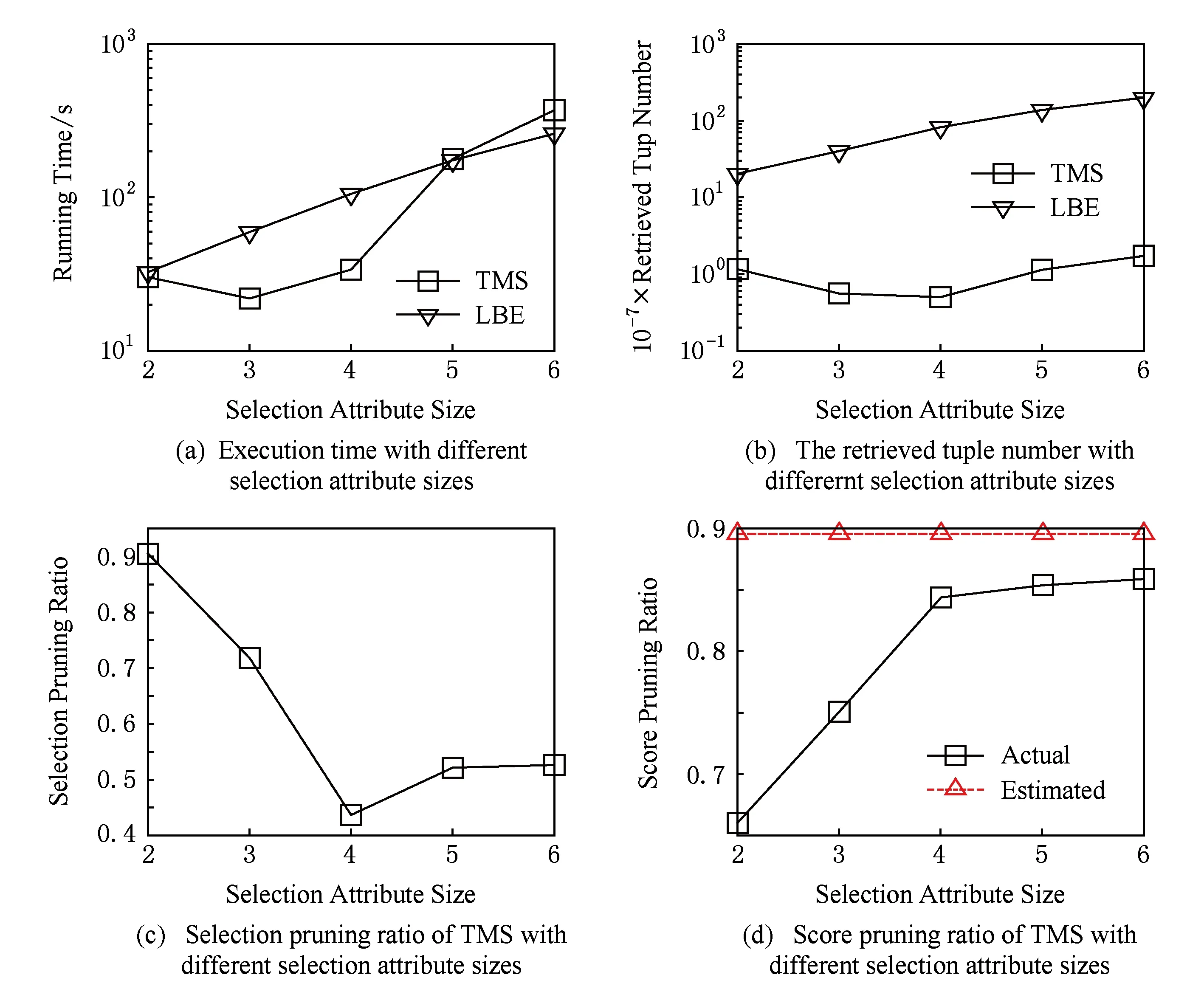
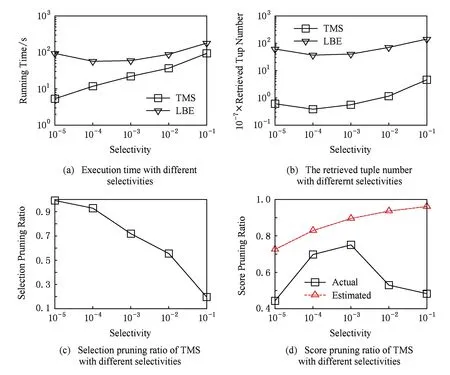
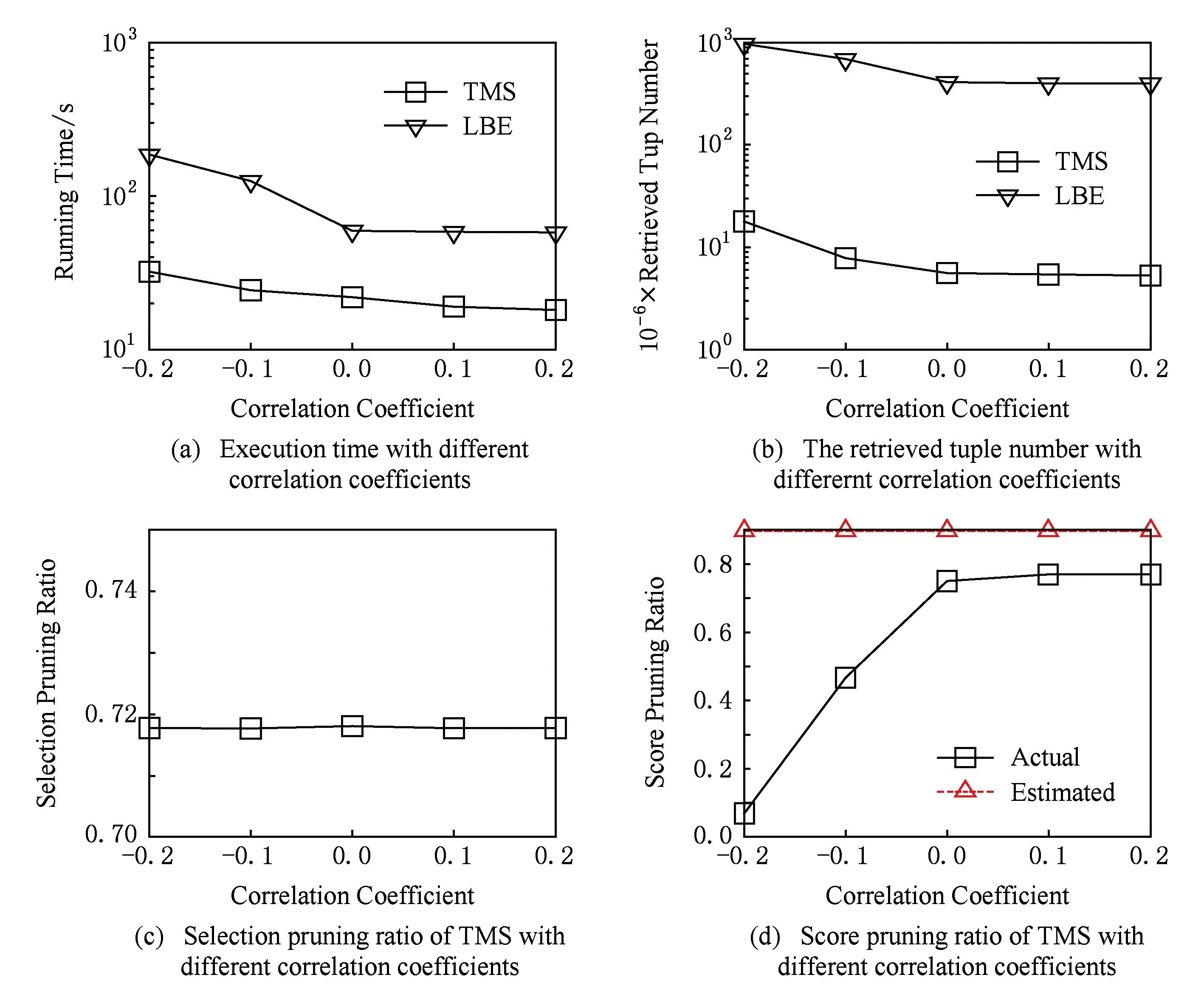
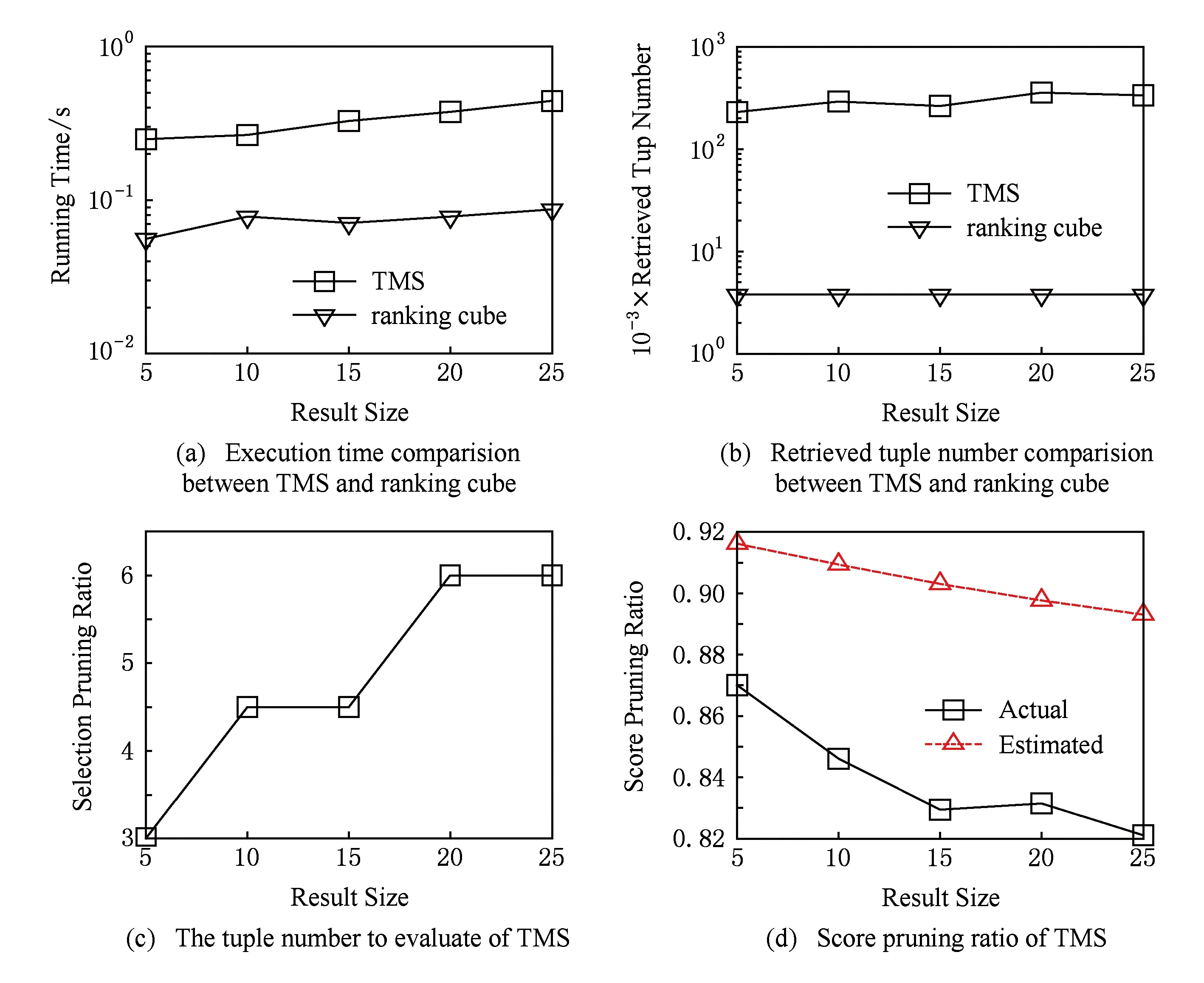
证明. 给定1≤h1 很明显,t1.PIptn 证毕. 在第1次排序后,令PBi[bh,…,eh]表示PBi中来自PRi[h]的元组.在评价多维选择时,TMS算法按照P[S1],P[S2],…,P[Sd]的顺序依次对PBi的元组执行多维选择评价,尽量利用对单个文件的顺序扫描来提高磁盘处理效率.在评价P[Sj]时,TMS算法从头开始扫描PBi中的元组,如果bh≤eh,TMS算法根据PBi[bh,…,eh]的PIptn属性的值,选择性地获得选择列表分片PSj[h]的第PIptn-OA[h]个元组来评价PBi[bh,…,eh]的对应元组的P[Sj]评价结果.在完成对P[S1],P[S2],…,P[Sd]的评价后,TMS算法根据Ai的值对PBi执行降序排序,我们就完成对PBi的元组的多维选择评价. 为返回分片集合FRi当前最大的属性Ai的值,TMS算法维护大小为NAF的最大堆结构FMHi.初始时,TMS算法读取FRi的每个分片的一个元组来填充FMHi. 在读取下一个满足条件的度量属性Ai的值时,TMS算法顺序读取PBi直到获得一个满足条件的元组t1,比较FMHi的当前根节点元组t2(假设t2∈FRi[h]),如果t1.Ai≤t2.Ai,TMS算法就获得t2作为当前轮的度量属性Ai的值,并读取FRi[h]的下一个元组填充FMHi,否则TMS算法就获得t1作为当前轮的度量属性Ai的值.如果PBi的元组被读取完毕,TMS算法重新执行填充操作.元组读取操作不断执行,直到返回查询结果或者相关度量列表分片的元组被遍历完毕. 下面,我们讨论如何确定缓冲区PBi的大小SZi的优化值.根据系统的性能和日常负载,系统首先设置缓冲区大小的上限MXSIZE,要求SZi≤MXSIZE. 下面,我们估计PDi的值,假设表T的属性均匀独立分布,数值选择属性的值域是[0, 1]. 令DPNOP表示没有多维选择情况下TMS算法的扫描深度,令NFh表示分片FRi[h]的元组数量,SELh表示分片PRi[h]对应的子空间和P相交的空间比例,TMS算法在FRi上的扫描深度FDi计算如下: 在其执行过程,TMS算法不需要读取选择列表分片集合PSj(1≤j≤d)的所有元组,只是选择性地读取指定位置的选择属性值来给出度量列表的候选元组的多维选择评价结果.很明显,需要执行多维选择评价和维护的度量列表候选元组的数量直接影响着TMS算法的性能.下面,我们在算法中提出剪切操作来有效减少需要处理的元组数量. 3.4 剪切操作 3.4.1 多维选择剪切 给定相关的度量列表分片集合PRi和FRi(1≤i≤m).∀t1∈FRi[h],t1肯定满足多维选择P,但是∃t2∈PRi[h],t2可能不满足P.这部分提出多维选择剪切策略来尽早丢弃那些不满足P的度量列表分片的候选元组. 考虑度量列表分片PRi[h](1≤i≤m),令其对应的选择属性子空间和多维选择P部分相交的子空间是ISTCh,那么多维选择剪切规则定义如下: ∀t(PI,Ai,PIptn)∈PRi[h],如果∃j(1≤j≤d),PSj[h](PIptn).Sj不在区间ISTCh[Sj]内,那么t不满足多维选择,其中PSj[h](PIptn).Sj表示文件PSj[h]中位置索引为PIptn的元组的Sj属性. 本文限制SAL的最大层次MXH,叶节点维护的选择属性子空间无法进一步划分,多维选择剪切方法就是在最底层的选择属性子空间中丢弃那些不满足条件的度量列表候选元组.本文采用指数间距前向bloom filter表和指数间距后向bloom filter表来有效实现多维选择剪切. 定义2. 给定选择列表分片PSj[h]及其对应的选择属性子空间HCh,EFBFTj,h和EBBFTj,h分别表示PSj[h]上的指数间距前向和后向bloom filter表,如果它们满足条件:1)|EFBFTj,h|=|EBBFTj,h|=lb(HCh[Sj].upp-HCh[Sj].low+1); 2)EFBFTj,h(b)表示在PSj[h].Sj∈[HCh[Sj].low,HCh[Sj].low+2b)的PSj[h]元组上利用属性PIptn构建的bloom filter,EBBFTj,h(b)表示在PSj[h].Sj∈(HCh[Sj].upp-2b,HCh[Sj].upp)的PSj[h]元组上利用属性PIptn构建的bloom filter. 我们可以分别将PSj[h]的元组按照选择属性Sj的值升序和降序排列,从而有效构建EFBFTj,h和EBBFTj,h. 已知,一个D维子空间SDS有2D个顶点,令该子空间的左下方和右上方的坐标分别是(bl1,bl2,…,blD)和(tr1,tr2,…,trD),给定子空间SDS的某一坐标为(cod1,cod2,…,codD)的顶点,其编号(b1b2…bD)定义如下: 令SDS(b1b2…bD)表示子空间SDS中具有编号为(b1b2…bD)的顶点,令SDS(b1b2…bD)[j]表示该顶点第j个坐标的值. Fig. 2 The illustration of selection pruning图2 选择剪切操作示例图 3.4.2 分数剪切 分数剪切操作利用评分函数单调性来剪切候选元组,从而减少多维选择评价和元组维护的费用. 先考虑一个简单模型来讨论分数剪切,即:查询不涉及多维选择,表T的元组数量是n2,并且表T的属性均匀独立分布.其中,我们为度量属性Ai(1≤i≤m)构建有序列表ALi.当执行Top-k查询时,我们对AL1,AL2,…,ALm执行round-robin扫描操作,且扫描深度是sdend=dp(n2,m,k).如图3所示,分数剪切操作需要确定存在深度exdep(≤sdend)和分数剪切深度spdep,使得ALi[1,…,exdep]有k个候选元组(pii,1,ai,1,ptni,1),(pii,2,ai,2,ptni,2),…,(pii,k,ai,k,ptni,k)满足存在条件:所有1≤k′≤k和1≤i′≤m(i′≠i),pii,k′∈πPI(ALi′[1,…,spdep]). Fig. 3 The illustration of score pruning图3 分数剪切示例图 给定exdep和spdep,∀t(PI,Ai,PIptn)∈ALi[(exdep+1),…,sdend],如果对所有1≤i′≤m(i′≠i),t.PI∉πPI(ALi′[1,…,spdep]),算法不需要维护候选元组t.因为,根据评分函数的单调性,T(t.PI)的分数肯定低于在ALi中满足存在条件的那k个元组的分数. 根据对简单模型的讨论,下面介绍如何在相关的度量列表分片集合上执行分数剪切.这里,我们同样假设度量属性A1,A2,…,Am均匀独立分布,需要注意的是,均匀独立分布假设只是为了计算方便,而并不影响TMS算法的执行. 已知,在不考虑多维选择时,TMS算法的优化分数剪切深度是spdepopt,我们需要计算在相关的度量列表分片上的分数剪切深度,换句话说,要获得spdepopt个满足多维选择的Ai属性的值需要从PRi和FRi分别读取的元组数量. 在对度量列表分片的扫描过程中,∀t1(PI,Ai,PIptn)∈PRi[h],如果所有1≤i′≤m并且i′≠i,t1.PI∈πPI(PRi′[h][1,…,pnph]),我们称t1满足存在条件,∀t2∈FRi[h],如果所有1≤i′≤m并且i′≠i,t2.PI∈πPI(FRi′[h][1,…,pnfh]),我们称t2满足存在条件. 令获得k个满足条件的元组时PRi[h1](1≤h1≤NAP)和FRi[h2](1≤h2≤NAF)扫描深度分别为edph1和edfh2,pnph1和pnfh2分别表示根据以上方法计算的PRi[h1]和FRi[h2]上的分数剪切深度,分数剪切规则定义如下: 给定度量列表分片集合PRi和FRi(1≤i≤m):1)∀t1∈PRi[h1][edph1+1,…,NPh1],如果对于所有1≤i′≤m并且i′≠i,t1.PI∉πPI(PRi′[h1][1,…,pnph1]),那么t1可以被剪切; 2)∀t2∈FRi[h2][edfh2+1,…,NFh2],如果对于所有1≤i′≤m并且i′≠i,t2.PI∉πPI(FRi′[h2][1,…,pnfh2]),那么t2可以被剪切. 本文采用指数间距bloom filter表来有效实现分数剪切. 定义3. 给定具有n个元素的度量列表Ri(PI,Ai,PIptn),EGBFTi是Ri上的指数间距bloom filter表,如果它满足条件:1)|EGBFTi|=lbn;2)EGBFTi(b)表示在Ri[1,…,2b]的PI属性上构建的bloom filter(1≤b≤lbn). 3.5 处理高维选择属性 本节介绍TMS算法如何处理高维选择属性的情况. 给定选择属性S1,S2,…,SD,选择属性网格SAL的第MXH层的子空间数量是(2D)MXH.如果D的值较大,TMS算法将生成大量的子空间,这也将导致文件系统的较大的维护费用,此外,给定同样的多维选择P,较大的D值也将使得TMS算法涉及到较多的相关分片.例如,给定D=12,MXH=3,TMS算法需要维护68 719 476 736个子空间. 在深入研究高维选择属性之前,我们先给出2个观察[5]: 观察1. 虽然选择属性的维度可能较大,但是提交的查询通常只涉及到较小数量的选择属性. 观察2. 在实际应用中,选择属性的查询频率通常服从Zipfian分布. 为处理高维选择属性,我们限制用来构建单个选择属性网格的选择属性数量,将S1,S2,…,SD划分成大小为GS的组,即G1={S1,S2,…,SGS},G2={SGS+1,SGS+2,…,SGS+GS},…,GDGS={SD-GS+1,SD-GS+2,…,SD},并且为每一个组构建选择属性网格.在这种情况下,TMS算法将维护数据表T的个副本,但是有效减少了需要维护的总的子空间数量.例如给定GS=3,MXH=3以及D=12,TMS算法只需要维护4个组,并且每个组只需要生成512个子空间. 根据观察2,如果磁盘空间大小有限,我们甚至可以不需要为每个组都构建选择属性网格,而是只选择具有较高查询频率的几个组.这样,我们不但可以有效减少需要的磁盘空间,而且还可以满足绝大多数的查询需求.例如给定GS=3,z=2以及D=12,只为第1个组构建选择属性网格也可以覆盖87%的查询. 给定多维选择P,TMS算法首先计算P和G1,G2,…,GDGS的交.不失一般性,令G1是具有和P最多的公共选择属性的组.例如给定G1={S1,S2,S3},G2={S4,S5,S6},G3={S7,S8,S9}以及G4={S10,S11,S12},P={(l1≤S1≤u1) and (l2≤S2≤u2) and (l4≤S4≤u4)},TMS算法将在G1构建的选择属性网格上执行.因为P中不包括S3,TMS算法利用{(l1≤S1≤u1)且(l2≤S2≤u2)且(minS3≤S3≤maxS3)}来确定相关子空间集合.当然,此时所有的相关子空间都是和P部分相交.接着,采用如3.3节和3.4节的方法来计算Top-k结果. 4.1 实验设置 本节评价算法的性能.我们利用Java语言实现TMS算法,jdk版本为jdk-7u21-windows-x64, 实验在LENOVO ThinkCentre工作站上执行(Intel®CoreTMi7-3770 CPU @ 3.40 GHz (8 CPUs)+32 GB memory+64bit Windows 7).实验所用的数据集合存储于Seagate Expansion STBV3000300 (3 TB).实验比较TMS算法、LBE和ranking cube的性能.实验不比较文献[3-4]中的方法,其原因在于,文献[3]中的方法实际上是计算多维空间上的k最近邻查询结果,文献[4]中的方法则只考虑只有一个数值属性的查询,并且要求预先给定需要的元组ID集合,从而文献[3-4]的方法从本质上不同于本文考虑的问题.对于TMS算法,考虑到文件系统的负载,选择属性网格的最大层次设置为3. 我们从不同方面评价TMS算法的性能:元组数量n、结果数量k、涉及到的选择属性数量d、涉及到的评价属性数量m、选择度s和相关系数p.实验参数设置如表2所示: Table 2 Parameter Settings 实验用来评价具有数值选择属性的表的Top-k查询如下: select * fromTwherel1≤S1≤u1andl2≤ S2≤u2and … andld≤Sd≤udorder byA1+ A2+…+Amlimitk. 其中,lj和uj分别表示多维选择在属性Sj上的上界和下界值. 类似地,实验用来评价具有类别选择属性的表的 Top-k查询如下: select * fromTwhereS1=a1andS2=a2 and … andSd=adorder byA1+A2+…+ Amlimitk. 其中,aj是属性Sj的特定值.当然,在类别选择属性上,选择属性网格结构不需要划分整个的数据空间,而是根据不同的属性组合来对数据表执行水平划分. 4.2 实验1:结果数量的效果 给定n=10×108,s=0.001,m=3,d=3,p=0,实验1评价不同结果数量下TMS算法的性能.如图4(a)所示,TMS算法比LBE算法快2.79倍.随着需要返回更多的结果数量时,LBE算法的执行时间增长较快,从48.956 s增长到68.598 s.相对而言,TMS算法的执行时间增长幅度较小,这是由于选择评价的费用占据了总的执行费用的大部分.如图4(b)所示,LBE算法读取的元组数量比TMS算法多71.68倍.这里,读取的元组数量是度量列表中读取的元组数量和选择列表中读取的元组数量之和.剪切操作的效果如图4(c)和图4(d)所示,其中,选择剪切比是被选择剪切操作丢弃的元组数量和读取的所有元组数量的比值,分数剪切比是被分数剪切操作丢弃的元组数量和未被选择剪切操作丢弃的元组数量的比值.由于选择属性和度量属性的独立分布,这里的分数剪切效果可以反应真实的分数剪切效果.如图4(c)和图4(d)所示,选择剪切操作可以丢弃72%的元组,分数剪切操作可以丢弃70%~77%元组.图4(d)中虚线表示理论的分数剪切比例.分数剪切的剪切比随着结果数量的增加而降低,这符合理论分析的结果. Fig. 4 The effect of result size图4 结果数量的效果 4.3 实验2:元组数量的效果 给定k=10,s=0.001,m=3,d=3,p=0,实验2评价不同元组数量下的TMS算法性能.如图5(a)所示,TMS算法比LBE算法快3.37倍.如图5(b)所示,LBE算法的读取的元组数量比TMS算法多80.99倍.图5(c)给出选择剪切比例基本保持在72%;图5(d)所示的分数剪切比例表示,分数剪切比在65%~78%之间.我们可以看到,随着元组数量的增加,分数剪切比逐渐增大,这也符合理论分析的结果. 4.4 实验3:选择属性数量的效果 给定n=10×108,k=10,s=0.001,m=3,p=0,实验3评价不同选择属性数量下的TMS算法性能.实验3假设多维选择在涉及到的选择属性上具有相等的选择度.在确定相关网格单元时,如果多维选择中的属性数量少于构建SAL使用的属性数量(例如多维选择不包括Sj属性,算法在多维选择条件上增加minSj≤Sj≤maxSj),否则,算法直接忽略选择条件上多余的选择属性.需要注意的是,这只是在确定相关网格单元,不影响算法的正确执行.如图6(a)所示,TMS算法比LBE算法快1.72倍.我们看到TMS算法的执行时间随着选择属性增大而迅速增长,给定选择度,更多的选择属性使得每个选择属性上的选择度增大,从而增加了涉及到的网格单元的数量.如图6(b)所示,LBE算法读取的元组数量比TMS算法多97.89倍.如图6(c)所示,多维选择涉及到更多的网格单元也使得选择剪切比例的下降.由于选择属性和度量属性的独立性,如图6(d)所示,当选择属性数量增大时,分数剪切比表现出增长趋势,但是真实剪切比仍然没有达到理论剪切比. Fig. 5 The effect of tuple number图5 元组数量的效果 Fig. 6 The effect of selection attribute size图6 选择属性数量的效果 4.5 实验4:度量属性数量的效果 给定n=10×108,k=10,s=0.001,d=3,p=0,实验4评价不同度量属性数量下的TMS算法性能.如图7(a)所示,TMS算法比LBE算法快3.98倍.随着涉及到的度量属性数量的增加,2个算法的执行时间都快速增长.如图7(b)所示,LBE算法读取的元组数量比TMS算法多137.96倍.根据计算公式dp(n,m,k),TMS算法的扫描深度与度量属性数量成指数关系,这也解释了TMS算法的读取的元组数量的快速增长.选择剪切操作的效果如图7(c)所示,其剪切比例基本保持在72%.根据3.4.2节的分析,更多的度量属性使得分数剪切比例下降,如图7(d)所示,实验结果符合理论分析结果. Fig. 7 The effect of ranking attribute size图7 度量属性数量的效果 4.6 实验5:选择度的效果 给定n=10×108,k=10,m=3,d=3,p=0,实验5评价不同选择度下的TMS算法性能.如图7(a)所示,TMS算法比LBE算法快5.88倍.当选择度增大时,LBE算法的执行时间首先下降,然后逐渐增加.这是由于,当选择度较小时,评价多维选择条件的费用较小,而读取有序度量列表的费用则较大,反之亦然.因此,图8(a)中的LBE算法的变化趋势是这2个因素的整合结果.当然,当选择度较大时,TMS算法涉及到更多的网格单元,从而增加了TMS算法的执行费用.如图8(b)所示,LBE算法读取的元组数量比TMS算法多72.11倍,并且读取元组数量的变化趋势类似于图8(a)的变化趋势.如图8(c)所示,更大的选择度使得查询涉及到更多的网格单元,从而减少了选择剪切比例.如图8(d)所示,分数剪切比首先增加,然后下降.这是由于,更大的选择度使得更多的元组满足查询条件,根据3.4.2节的分析,更多的元组满足查询条件也使得分数剪切比例增加,这解释了s=10-5到s=10-3的变化趋势,但是,随着选择度进一步提高,相关的网格单元的数量也增长较快,分配到每个单元的剪切深度就相应减少,采用EGBFT元组执行分数剪切操作使得剪切深度扩展到2的最小的指数间距上界,从而降低分数剪切比例. 4.7 实验6:相关系数的效果 给定n=10×108,k=10,s=0.001,m=3,d=3,实验6评价不同相关系数下的TMS算法性能.如图9(a)所示,平均来看,TMS算法比LBE算法快3.99倍.很明显,随着相关系数的增大,2个算法的执行时间都下降,但是下降的速率不同,这取决于不同算法的执行方法.如图9(b)所示,LBE算法读取的元组数量比TMS算法多73.22倍.如图9(c)所示,选择剪切比例基本维持在72%.从图9(d)看到,随着相关系数从负值增大到正值,分数剪切的比例迅速增大,从不到10%增长到接近80%. Fig. 8 The effect of selectivity图8 选择度的效果 Fig. 9 The effect of correlation图9 属性相关的效果 4.8 实验7:和ranking cube的比较 给定n=10×108,d=3,m=3,p=0,实验7比较在不同结果数量下的TMS算法和ranking cube算法的性能.在实验7中,选择属性是类别类型的,并且每个选择属性的基数设置为8,那么满足多维选择条件的元组比例是1512.在ranking cube的每个单元中,元组根据基于几何的划分来进行组织,我们为每个度量属性的值域设置8个等长的桶.为提供ranking cube的优化性能,我们只保留每个元组的查询处理需要的属性.如图10(a)所示,ranking cube比TMS算法快4倍.图10(b)解释了ranking cube的执行时间的优势的原因,该算法的IO费用比TMS算法少了一个数量级.图10(c)给出了需要执行多维选择评价的元组数量,我们看到,该数值随着结果数量的增加而增大.由于在类别选择属性上,相关的元组都满足多维选择,所以实验7不提供多维选择剪切的结果.如图10(d)所示,虽然随着结果数量的增加其剪切比例降低,TMS算法的分数剪切可以丢弃超过82%的候选元组. Fig. 10 The comparison with ranking cube图10 和ranking cube的比较 作为多个领域中一种重要的数据操作,Top-k查询得到了研究人员的广泛关注[1].在海量数据环境中,Fagin等人[6]提出NRA算法来处理只支持顺序读的Top-k查询.研究人员也提出一系列对于NRA算法的改进,包括LARA算法[7]、TBB算法[8]和TKEP[9]等.研究人员还提出利用索引结构[11-13]或者视图[14-15]来处理Top-k查询.但是,大多数的现有方法都没考虑多维选择Top-k查询问题. Bruno等人[3]把Top-k查询转换为数据库上的范围查询,从而可以利用现有数据库技术来直接回答Top-k查询,该方法实际上执行的是kNN查询,不同于本文考虑的多维选择查询.Stupar等人[4]考虑处理基于集合选择的Top-k查询,即预先给定需要的元组ID集合,然后计算满足条件的查询结果.但是,该方式只考虑一个数值属性的情况,而且基于集合的选择条件也过于特殊.Dong等人[5]考虑具有类别选择属性和数值度量属性的多维选择Top-k查询,在选择属性上构建ranking cube来分布元组,每个单元内的元组采用基于几何信息划分方式组织成不同基本块.查询处理阶段,算法从最可能包括查询结果的基本块开始扫描,从而快速计算查询结果.但是,ranking cube方法只能处理类别选择属性,无法处理一般情况下(数值选择属性)的多维选择Top-k查询. 本文分析发现,现有方法无法有效处理海量数据上多维选择Top-k查询.因此,本文提出一个新的基于有序列表的TMS算法,该算法利用层次化的选择属性网格来对数据执行水平划分,并且每个网格单元对应的分片按列模式存储.给定多维选择,TMS算法首先确定相关的网格单元,这有效减少了需要读取的元组数量.TMS算法利用双排序方法来渐进评价度量列表分片元组的多维选择结果,并提出有效的选择剪切和分数剪切操作来进一步减少需要处理的元组数量.本文实验表示TMS算法比现有算法具有较大的优势. [1]Ilyas I, Beskales G, Soliman M. A survey of top-kquery processing techniques in relational database systems[J]. ACM Computing Survey, 2008, 40(4): Article No 11 [2]Han Xixian, Li Jianzhong, Gao Hong. Efficient top-kretrieval on massive data[J]. IEEE Trans on Knowledge and Database Engineering, 2015, 27(10): 2687-2699 [3]Bruno N, Chaudhuri S, Gravano L. Top-kselection queries over relational databases: Mapping strategies and performance evaluation[J]. ACM Trans on Database Systems, 2002, 27(2): 153-187 [4]Stupar A, Michel S. Being picky: Processing top-kqueries with set-defined selections[C]Proc of the 21st ACM Int Conf on Information and Knowledge Management. New York: ACM, 2012: 912-921 [5]Dong Xin, Han Jiawei, Cheng Hong, et al. Answering top-kqueries with multi-dimensional selections: The ranking cube approach[C]Proc of the 32nd Int Conf on Very Large Data Bases. New York: ACM, 2006: 463-474 [6]Fagin R, Lotem A, Naor M. Optimal aggregation algorithms for middleware[J]. Journal of Computer and System Sciences, 2003, 66(4):614-656 [7]Mamoulis N, Yiu M, Cheng K, et al. Efficient top-kaggregation of ranked inputs[J]. ACM Trans on Database Systems, 2007, 32(3): Article No 19 [8]Pang H, Ding Xuhua, Zheng Baihua. Efficient processing of exact top-kqueries over disk-resident sorted lists[J]. The VLDB Journal, 2010, 19(3): 437-456 [9]Han Xixian, Li Jianzhong, Yang Donghua. Supporting early pruning in top-kquery processing on massive data[J]. Information Processing Letter, 2011, 111(11): 524-532 [10]Han Xixian, Li Jianzhong, Gao Hong. An efficient top-kdominating algorithm on massive data[J]. Chinese Journal of Computers, 2013, 36(10): 2132-2145 (in Chinese)(韩希先, 李建中, 高宏. 一种有效的海量数据top-kdomi-nating查询算法[J]. 计算机学报, 2013, 36(10): 2132-2145) [11]Heo J, Cho J, Whang K. Subspace top-kquery processing using the hybrid-layer index with a tight bound[J]. Data & Knowledge Engineering, 2013, 83: 1-19 [12]Zou Lei, Chen Lei. Pareto-based dominant graph: An efficient indexing structure to answer top-kqueries[J]. IEEE Trans on Knowledge and Data Engineering, 2011, 23(5): 727-741 [13]Lee J, Cho H, Hwang S. Efficient dual-resolution layer indexing for top-kqueries[C]Proc of the 28th IEEE Int Conf on Data Engineering. Los Alamitos, CA: IEEE Computer Society, 2012: 1084-1095 [14]Das G, Gunopulos D, Koudas N, et al. Answering top-kqueries using views[C]Proc of the 32nd Int Conf on Very Large Data Bases. New York: ACM, 2006: 451-462 [15]Xie Min, Lakshmanan L, Wood P. Efficient top-kquery answering using cached views[C]Proc of the 16th Int Conf on Extending Database Technology. New York: ACM, 2013: 489-500 Han Xixian, born in 1981. PhD, associate professor. His main research interests include massive data management and data intensive computing. Liu Xianmin, born in 1984. PhD, lecturer. His main research interests include massive data computing and data quality management. Li Jianzhong, born in 1950. Professor, PhD supervisor. Fellow member of CCF. His main research interests include data-intensive computing, wireless sensor networks and CPS. Gao Hong, born in 1966. Professor, PhD supervisor. Her main research interests include data-intensive computing, wireless sensor networks and CPS. TMS: An Novel Algorithm for Top-kQueries with Multi-Dimensional Selections on Massive Data Han Xixian, Liu Xianmin, Li Jianzhong, and Gao Hong (SchoolofComputerScienceandTechnology,HarbinInstituteofTechnology,Harbin150001) In many applications, top-kquery is an important operation to return a set of interesting points among potentially huge data space. Usually, a multi-dimensional selection is specified in top-kquery. It is found that the existing algorithms cannot process the query on massive data efficiently. A sorted-list based algorithm TMS (top-kwith multi-dimensional selection) is proposed to process top-kquery with selection condition on massive data efficiently. TMS employs selection attribute lattice (SAL) of hierarchical structure to distribute tuples and obtains a horizontal partitioning of the table. Each partition is stored in column-oriented model and the lists of ranking attributes are arranged in descending order of attribute values. Given multi-dimensional selection, the relevant lattice cells are determined by SAL and this reduces the number of the retrieved tuples significantly. Double-sorting operation is devised to perform progressive selection evaluation. The efficient pruning is developed to discard the candidates which do not satisfy selection condition or score requirement. The extensive experimental results show that TMS has a significant performance advantage over the existing algorithms. top-kwith multi-dimensional selection (TMS) algorithm; sorted list; selection attribute lattice (SAL); progressive selection evaluation; pruning 2015-06-30; 2015-10-29 国家“九七三”重点基础研究发展计划基金项目(2012CB316200);国家自然科学基金项目(61502121,61402130,61272046,61190115,61173022,61033015);山东省自然科学基金项目(ZR2013FQ028);山东省科技重大专项基金项目(2015ZDXX0210B02) This work was supported by the National Basic Research Program of China (973 Program) (2012CB316200), the National Natural Science Foundation of China (61502121, 61402130, 61272046, 61190115, 61173022, 61033015), the Natural Science Foundation of Shandong Province of China (ZR2013FQ028), and the Major Projects of Science and Technology of Shandong Province (2015ZDXX0210B02). TP311
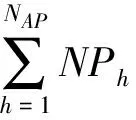

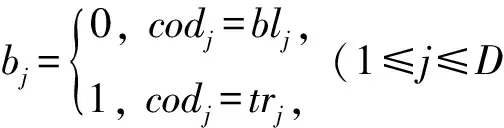
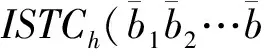







4 性能评价


5 相关工作
6 结 论





