支持室内障碍空间的DSP-Topk查询优化算法研究
李博涵 张 潮 李东静 许建秋,2 夏 斌 秦小麟,2
1(南京航空航天大学计算机科学与技术学院 南京 210016)2(江苏省软件新技术与产业化协同创新中心 南京 210016)3 (江苏易图地理信息科技股份有限公司 江苏扬州 225000) (bhli@nuaa.edu.cn)
支持室内障碍空间的DSP-Topk查询优化算法研究
李博涵1,2,3张 潮1李东静1许建秋1,2夏 斌1秦小麟1,2
1(南京航空航天大学计算机科学与技术学院 南京 210016)2(江苏省软件新技术与产业化协同创新中心 南京 210016)3(江苏易图地理信息科技股份有限公司 江苏扬州 225000) (bhli@nuaa.edu.cn)
多目标优化查询是目前移动对象数据管理的研究热点.多目标优化查询过程中,用户关心的目标对象属性可能依赖于其他移动对象,因此移动对象之间的相互影响将导致目标对象属性存在不确定性.已有的多目标优化算法需要遍历所有目标对象,且不能有效支持目标对象属性的动态变化.基于以上问题,提出了一种有效的应用于障碍空间的多目标优化算法DSP-Topk (dynamic and support pruning Topk),该算法采用可视区域模型处理障碍空间中移动对象的距离计算,利用基于最大夹角差的可视区域方法,提高了计算距离的效率.进而,利用动态调整机制解决目标对象属性的不确定性,预处理的裁剪策略提高了算法效率.实验结合商场真实商品数据集进行测试,与已有的Topk和DS-Topk算法对比表明:所提算法在查询效率上有显著提高,验证了算法的有效性.
移动对象;多目标优化;不确定性;裁剪;动态调整
随着定位技术和无线传感器网络技术的不断发展,位置服务在人们的日常生活中扮演着越来越重要角色[1].位置服务的质量依赖于对移动对象数据的有效管理,这里的移动对象是广义上的移动对象,指含有不断变化属性的数据对象,属性包含空间属性和非空间属性[2].多目标优化查询是移动对象数据管理中的研究热点,如Topk[3],Skyline[4],NN[5],KNN[6]等.多目标优化查询可以帮助用户解决在一定条件约束下,希望查询结果在多个目标下达到最优的问题[7].
已有的移动对象数据管理研究主要集中在室外,包括自由空间中的移动对象和基于路网约束的移动对象[8-9].然而有数据统计表明人们活动的区域和时间约有80%处于室内环境,如办公楼、商场、地铁站等,因此针对移动对象在室内环境下的研究具有现实意义[10].在室内环境中移动对象多目标优化查询具有众多的应用场景.比如众多的大型商场和购物中心,如南京万达广场占地面积达39万m2、一站式购物中心达27万m2、商场内的店铺多达1 000家.如何在众多店铺中帮助顾客找到距离近、优惠多、顾客评价好的店铺;在火车站、机场、医院等人群密集的场所发生意外情况时,帮助人们在距离、安全系数等目标约束下选择1个最佳的逃生方式和路线.这些都属于室内移动对象多目标优化查询的研究范畴.还有一些多目标优化查询的过程中,用户对某些关心的目标属性设置了约束条件.如在进行店铺推荐过程中用户希望所推荐的店铺距离自己当前位置100 m以内,在这里100 m就是用户针对距离这个目标提出的阈值.
室内环境相对于室外,空间拓扑结构更加复杂,移动对象之间的距离计算难度更大,传统的距离算法已不能很好地适应于室内环境[11].近年来,针对障碍空间中的移动对象数据管理已经取得了一定的成果,提出了3D几何网络模型(3D geometric network model)[12]和基于连通图(accessibility base graph)的门模型[13]等代表性模型,这些模型很好地将现实物理世界抽象为简单易懂的几何模型,但是这些模型忽略了移动对象与障碍空间的位置关系,导致没有障碍物阻挡的移动对象之间的距离也需要通过复杂的计算得到结果,降低了算法的性能.可视区域模型区分了移动对象与障碍空间的位置关系,但是已有的可视区域生成算法(如多次穿越障碍算法MTO)[14]需要连续扫描,重复穿越障碍空间导致可视区域生成算法效率较低.
在移动对象多目标优化查询研究方面,已有的移动对象多目标优化算法只能返回1个最优解候选集(如Skyline查询)或者需要遍历所有目标对象(如Topk查询)从而导致效率较低.另外在查询过程中,移动对象之间的互相影响可能导致目标对象的属性值发生改变,存在着不确定性,因此使用静态的原始数据会导致查询结果的不准确.如何将移动对象多目标优化查询适应于室内障碍环境,特别当目标对象属性发生动态改变时还能准确提供最优化查询结果成为研究的出发点.针对这些问题,提出了一种改进的适用于障碍空间的移动对象多目标优化查询算法DSP-Topk(dynamic and support pruning Topk).算法利用基于最大夹角差的可视区域算法计算移动对象之间的最短距离,确定移动对象的空间属性,此外DSP-Topk支持目标对象属性值的动态变化,采用预处理的裁剪策略避免对所有目标对象进行遍历,提高算法效率.
本文主要贡献有3点:
1) 采用预处理的裁剪策略和对候选集的动态调整方法得到改进的多目标优化查询算法DSP-Topk;
2) 为更好地适应室内障碍环境,利用基于最大夹角差的可视区域算法,提高了移动对象之间距离计算的性能,使得DSP-Topk算法能很好地解决室内障碍环境中移动对象多目标优化查询问题;
3) 结合商场真实的商品数据集进行测试,检验了算法的有效性.
1 相关工作
1.1 障碍空间中的距离计算
室内环境的空间方向、拓扑和距离关系由于障碍物的存在而变得更加复杂.不同于室外环境,在室内环境下移动对象之间距离相对较近,移动对象的距离之间受到障碍物的约束,当移动对象之间有障碍物的阻挡时,不能简单地将距离抽象为2点之间的欧氏距离进行近似计算[15].文献[13]提出基于连通图的室内空间模型,以门作为节点记录各个门之间最短距离,计算2个对象最短距离时,只需找到与目标对象最近的1扇门,将移动对象与门之间的距离和门所记录的距离相加就是2个移动对象之间的最短距离.文献[16]在欧氏空间中提出了确定对象的安全区域概念,所谓安全区域即空间中某一些目标对象结果集对应的1个空间范围,1个室内空间可以有多个安全区域.在安全区域内,所有查询对象具有相同的最近邻查询结果.当查询点在安全区域内移动时,不再需要重复查询.因而预先生成安全区域可以节省大量的实时计算开销,但不足之处是对于那些空间位置范围变化较大的移动对象需要不断更新安全区域.文献[14,17-18]提出可视区域的概念,在可视区域内查询对象与目标对象之间的最短距离不受障碍空间的影响,但是传统的可视区域算法效率较低.如多次穿越障碍算法MTO需要连续扫描查询对象和障碍空间,重复穿越障碍空间导致算法效率较低.
1.2 多目标优化查询
生活中,许多问题都是有相互冲突和影响的多个目标组成.人们经常会遇到使多个目标在给定区域同时尽可能最佳的优化问题,也就是多目标优化问题.优化问题存在的优化目标超过1个并需要同时处理,就成为多目标优化问题.传统的移动对象多目标优化的问题通常有3种解决方法[19]:
1) Pareto方法(Skyline查询)[20],改进的Skyline查询算法,如NN[5],BBS[21-22]等.Skyline查询返回1个最优解的候选集,但是当返回的结果规模较大时,并不能很好地为用户提供决策.
2) 词典序的方法,它为目标对象的不同属性设置了不同级别的优先级,在进行选择的过程中,按照优先级从高到低进行比较,如果高级别属性值相同,再比较低一级的属性值,直到得到结果.这种方法的优点在于最终能给用户1个确定的结果,但是在某些特殊情况下,这种方法并不能返回理想结果.比如有A,B两个待比较对象,它们分别有a,b,c三个属性,属性的优先级为a>b>c.其中A对象只是在a属性上略优于B对象,但在b和c属性上远远差于B,此刻词典序的方法仍然认为最优选择是A,但是在现实中用户可能更加倾向于选择B.
3) 将多目标优化问题转化为单目标优化问题,将不同的属性用一种统一的参考量来描述,用户可以对不同的属性依据自己的偏好设置不同的权值,然后对不同对象之间进行计算,找出最佳选择.后续有学者不断改进Topk算法,如DS-Topk相比于Topk只在最终对候选目标对象进行排序选择,DS-Topk在前期进行一部分排序裁剪,减少了查询对象的规模,提高了算法的效率.虽然DS-Topk算法进行了预裁剪,但是不支持用户提出的阈值二次裁剪,且当查询过程中存在移动对象之间的互相影响导致目标对象的属性发生动态变化时也不适用.
在提高多目标优化算法的查询效率上,也有2类解决方法:1)通过不断改进索引结构来提高查询效率,文献[23]提出了一种基于索引的高效k-支配的Skyline查询;2)通过减少IO访问次数来提高查询效率.文献[24]基于排序机理的算法提出了一种新的度量空间中的Skyline查询MkRS(metric Topk reverse Skyline);文献[25]利用Topk和Skyline各自的特点,提出了包括Topk-TBBST,Topk-dMBBS,Topk-wMBBS算法.这些算法可以有效提高Cache的命中率并减少IO数,但是都忽略了目标对象属性的不确定性对查询结果的影响.基于以上问题,提出了一种支持目标对象动态调整的、可裁剪的多目标最优化算法DSP-Topk算法.它通过对目标对象的裁剪,减小目标对象集合的规模,从而降低算法执行的时空开销;通过改进算法实现动态调整机制,使其适应于目标对象属性的动态变化.
2 基础知识
2.1 问题描述
给出2个不同的室内环境下移动对象多目标优化的查询实例.在图书馆内,学生希望找到距离自己最近的空位且该座位附近有可用的电源插座;某大型商场内,购物区内的顾客查找餐馆,希望餐馆距离近、价格实惠、排队人数少.在这2个查询中其他学生的离开或者提前使用插座会改变目标对象座位的属性值;商场内其他顾客进出餐馆,使目标对象餐馆在排队人数这个属性上发生动态变化.通过这些实例甚至更多的室内场景查询实例可知,看似与查询无关的其他移动对象,可能使目标对象在用户关心的某些属性上发生动态变化,从而使目标对象的属性具有不确定性.
将室内障碍环境和支持移动对象属性动态调整的多目标优化查询相结合将面临2个挑战:
1) 现有的室内障碍环境中移动对象距离计算模型,没有区分移动对象与障碍空间的位置关系,导致没有障碍物阻挡的移动对象之间的距离也需要通过复杂的计算得到结果;
2) 现有的移动对象多目标最优化算法以某一时刻的静态数据作为查询依据,缺乏考虑在查询过程中目标对象的属性值发生改变导致查询结果不确定的情况.
针对上述问题,利用为顾客作餐馆推荐为例,解决思路主要分为3步:
1) 对商场空间布局建立模型,利用可视区域的算法,确定顾客和所有餐馆的空间距离,将这个距离作为餐馆的空间属性;
2) 对所有餐馆进行预处理,利用裁剪策略缩小餐馆查询的规模;
3) 根据餐馆属性的实际动态变化情况采取动态调整策略和阈值二次裁剪重新生成新的候选集合,最后对候选集合进行排序得到最优推荐对象.
2.2 障碍空间中多目标优化查询的形式化定义
为便于问题描述,利用为顾客作餐馆推荐为查询实例,结合餐馆所在的商场的室内拓扑结构,给出移动对象多目标优化和室内场景下基于可视区域的距离计算的相关形式化定义.
将移动对象多目标优化查询引入到室内障碍场景,移动对象之间距离计算成为1个难以规避的问题.室内障碍环境下,空间拓扑结构更加复杂,距离计算的好坏直接影响了移动对象多目标优化查询算法的性能.为解决距离计算的复杂性,DSP-Topk算法采用最大夹角差的可视区域方法计算移动对象之间的距离.其中可视区域模型构造如下:
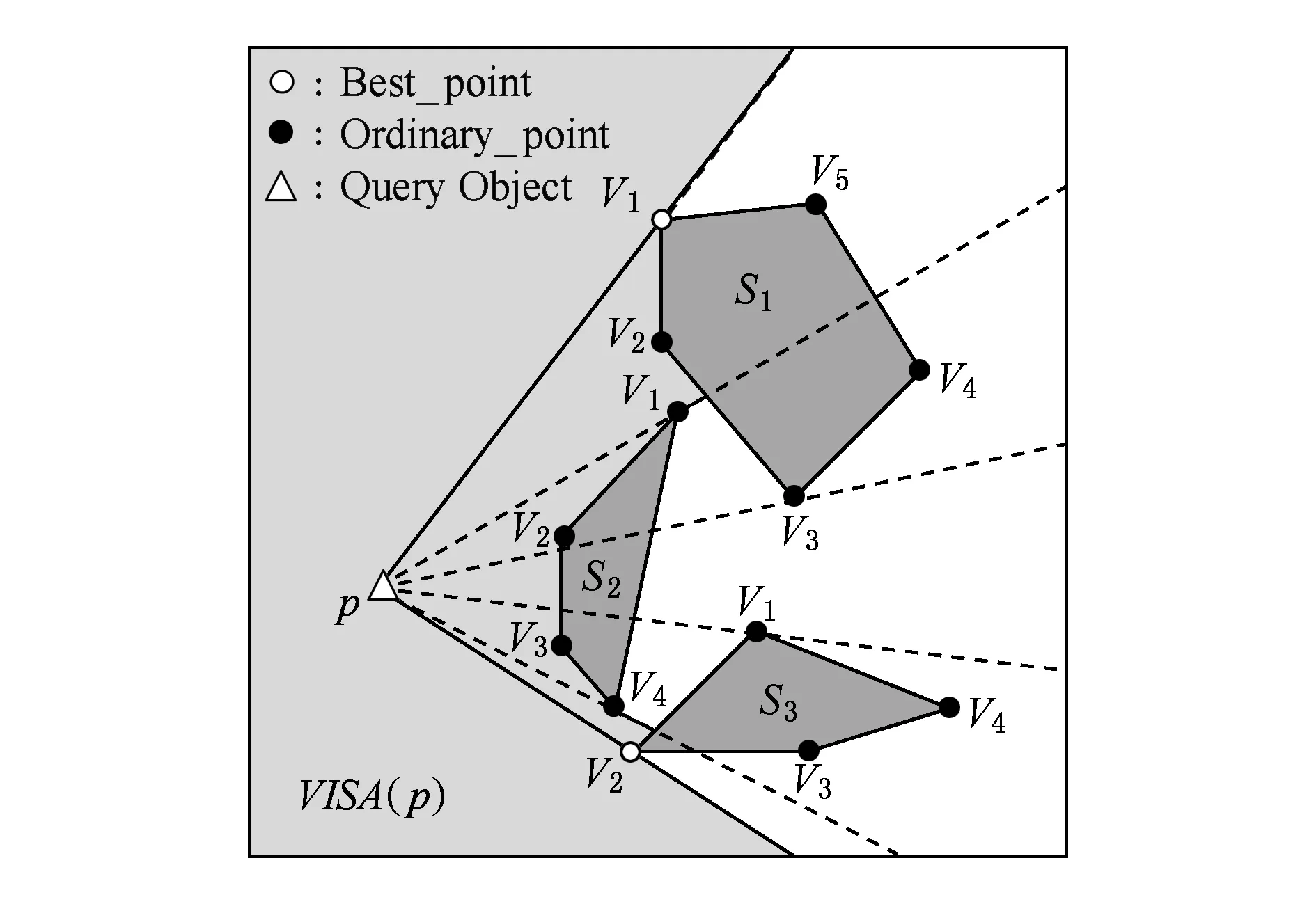
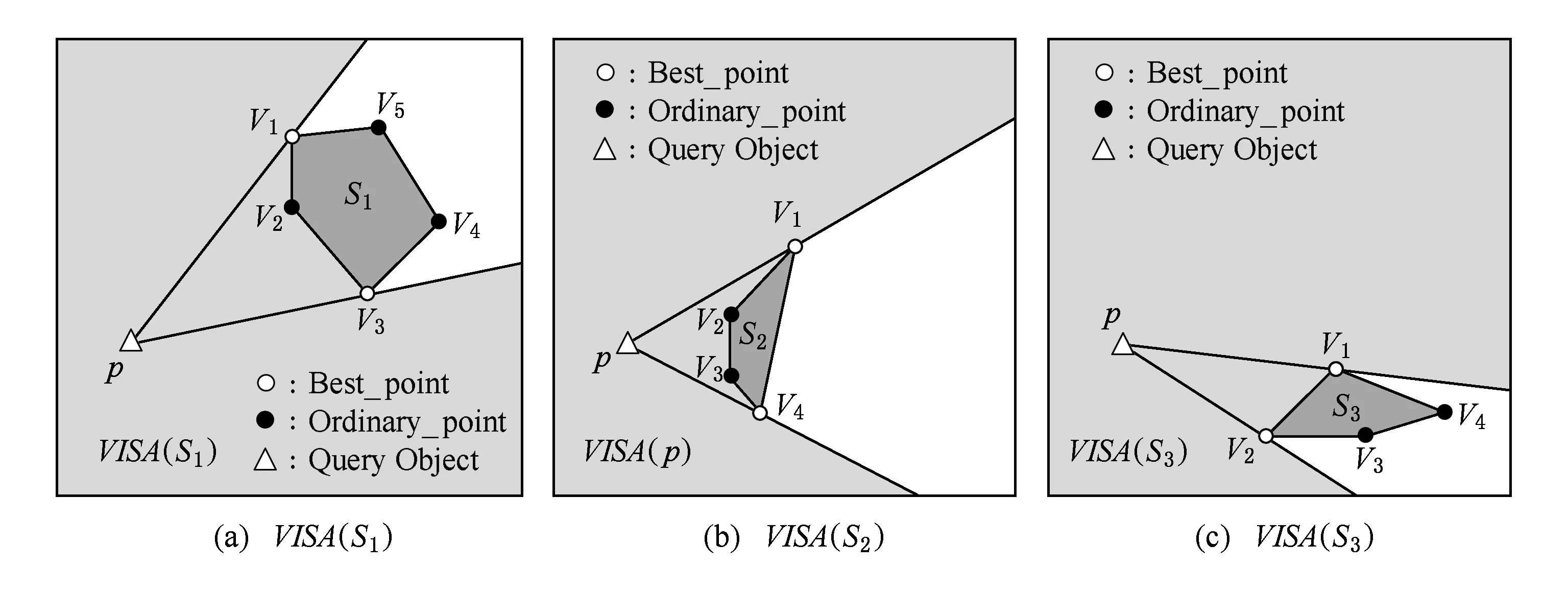
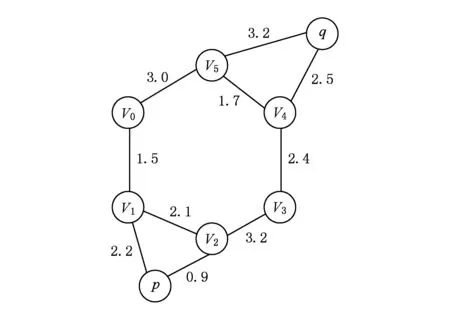
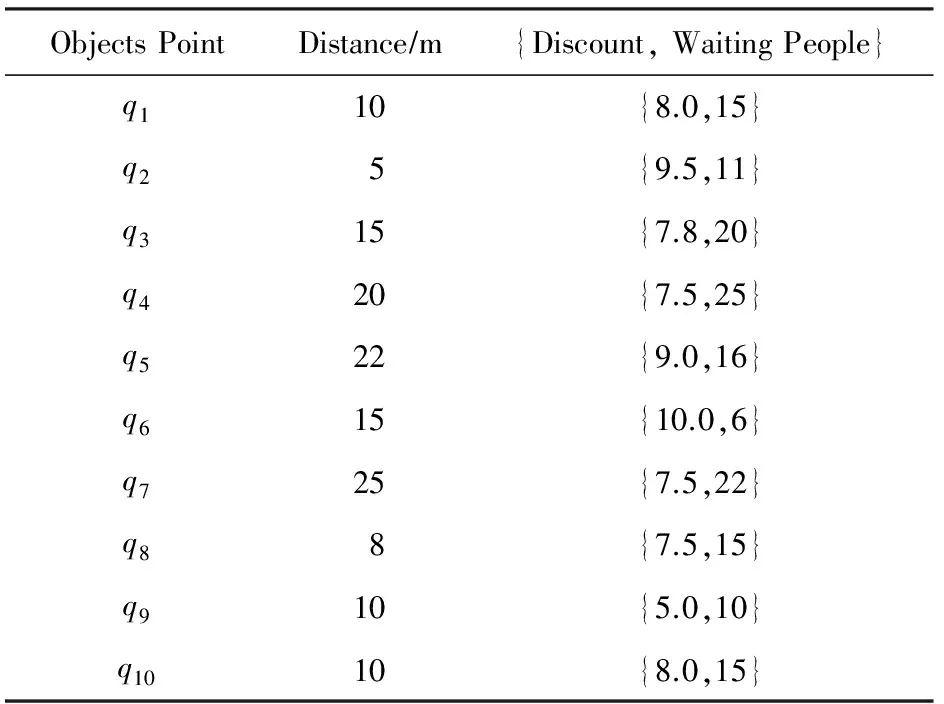
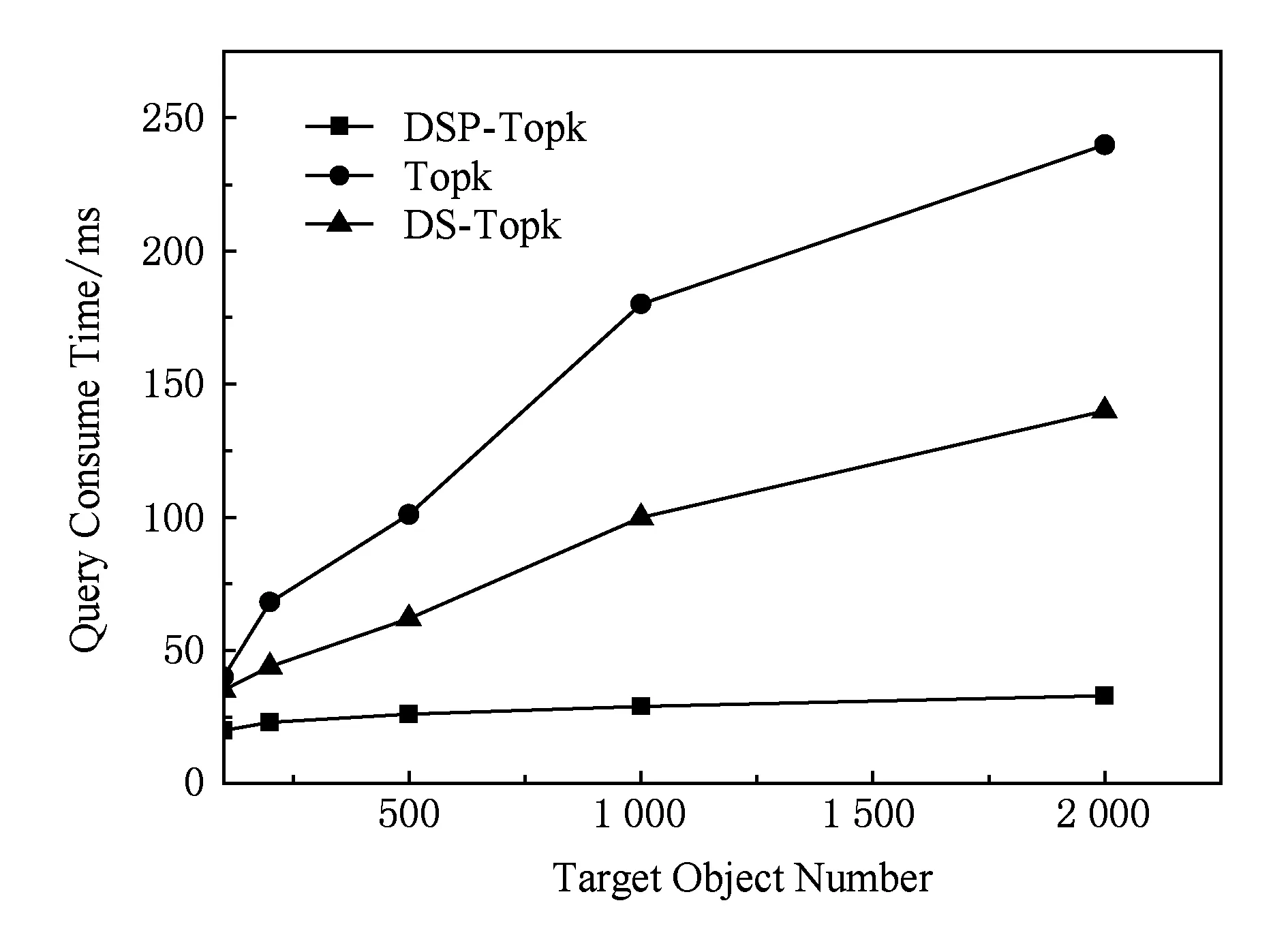
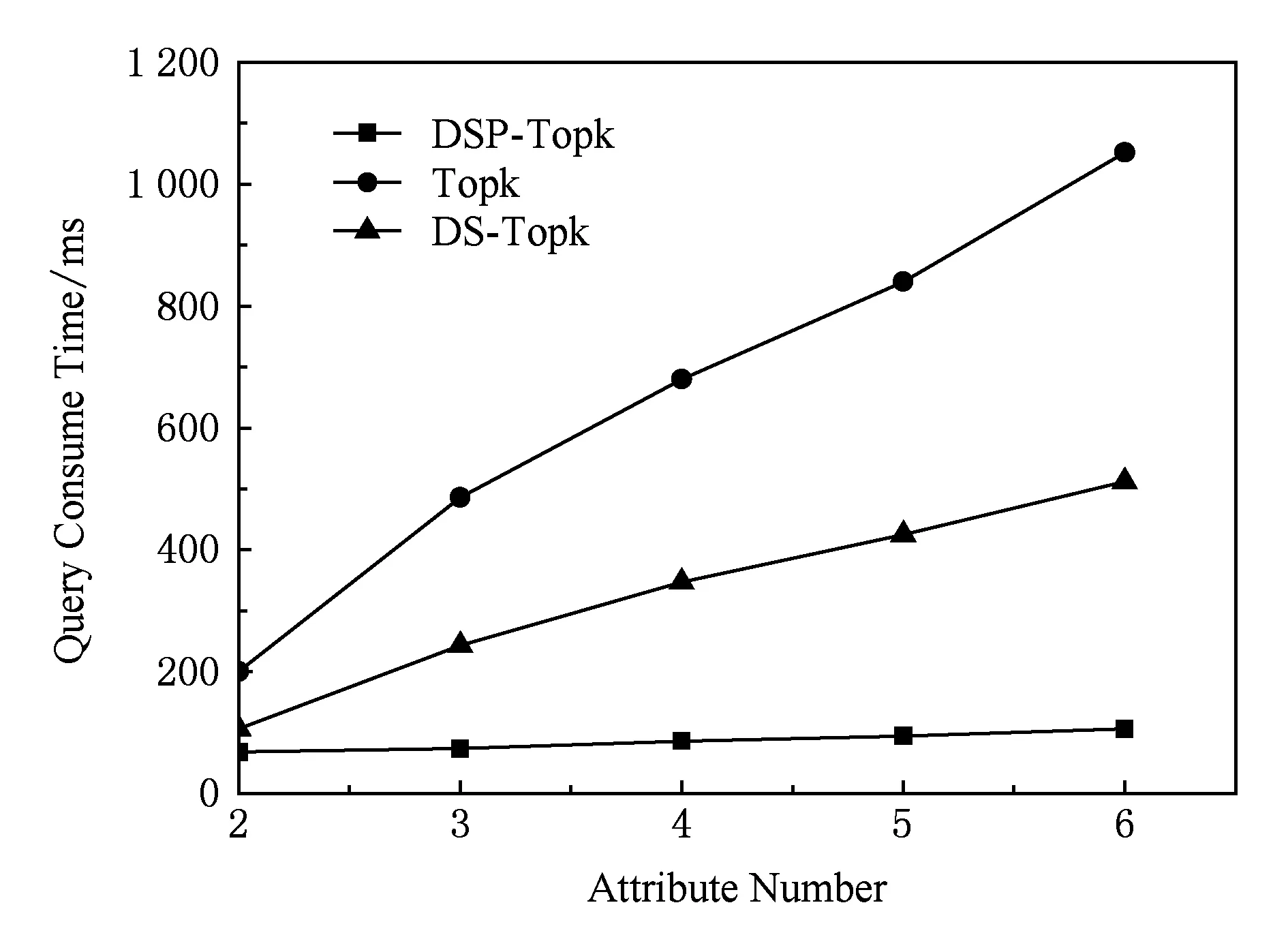
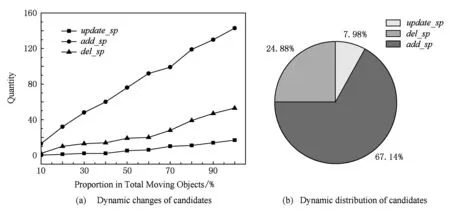
假设室内空间为I,具有n个移动对象构成集合Q={q1,q2,…,qn},2 将查询对象与移动对象统一抽象为同一平面上的点,对于现实世界中移动对象之间的空间距离表示为平面上点之间的距离.移动对象作为多目标优化的目标对象,其空间距离包含2种情况:1)如果移动对象分布在同一平面上,则空间距离可直接计算;2)反之需要加上移动对象之间所在平面的距离(如楼梯的长度和电梯的高度). DSP-Topk算法采用可视区域(visible area)的方法计算障碍空间中移动对象之间的最短距离.查询对象p的可视区域利用最大夹角差的方法确定,其中关于a,b两点与原点之间的夹角 (1) 查询对象p的可视区域记为VISA(p),其定义如下: 定义1. 可视区域. 在室内环境下,每个查询对象p都有1个可视区域VISA(p)与之对应,区域VISA(p)中任意一点与点p的连线都不与障碍物相交,其中VISA(p)具有3个性质: 性质1.VISA(p)是1个封闭的空间,是由室内空间的边界和障碍物的边界所组成的. 性质2. 在二维平面下VISA(p)的面积小于等于室内空间的横截面积,在3维空间下VISA(p)的体积小于等于室内空间的体积. 性质3. 根据目标对象是否在可视区域内,可分为2种情况:1)在VISA(p)中的目标对象qi与查询对象p的最短距离是二者之间的欧氏距离即mindis=|p,qi|;2)不在VISA(p)的目标对象qi与查询对象p的最短路径通过障碍物所对应的多边形Si的一些顶点,即 mindis=|p,Vi|+|Vi,Vj|+…+|Vn,p|. 例如前面提到的顾客在商场中希望找到这样1个餐馆,它距离自己较近、价格实惠以及排队人数少.该场景可以用图1表示,整个平面就是商场,查询点p就是顾客,目标对象集合{q1,q2,…,q10}是餐馆所抽象的点集合,餐馆具有的空间属性就是与顾客之间的距离,非空间属性就是价格、排队人数.图1中的浅色阴影区域就是顾客p的可视区域VISA(p),可以发现部分餐馆在可视区域VISA(p)中,如q1,q2,也有部分餐馆不在VISA(p)中如q4,q5. Fig. 1 VISA of query object p on single obstacle图1 单个障碍物下查询对象p的可视区域 如图2、图3所示,当障碍空间内具有多个障碍物时,需要对每个多边形的可视区域VISA(Si)求交集得到可视区域VISA(p). 在图2中障碍空间中有多边形S1,S2,S3.这种情况下VISA(p)=VISA(S1)∩VISA(S2)∩VISA(S3)其中VISA(S1),VISA(S2)和VISA(S3)是查询对象p相对于每个多边形所求的可视区域如图3所示. Fig. 2 VISA of query object p on multi-obstacles图2 多个障碍物下查询对象p的可视区域 Fig. 3 VISA of single convex polygon on multi-obstacles图3 多障碍物下单个多边形可视区域示意图 移动对象多目标优化查询可以帮助用户解决在一定条件约束下希望查询结果在多个目标下达到最优的问题.用户关心的多个目标对应于目标对象的多个属性,关于目标对象多属性的定义如下: 定义2. 目标对象多属性.移动对象多目标优化查询的对象称为目标对象,目标对象具有的属性包含的空间属性和非空间属性.空间属性是指目标对象与查询对象在障碍空间中的最短距离;非空间属性是指对象除空间信息外含有的其他属性. 当目标对象的规模较大时,对初始的候选集合进行裁剪处理能提高查询效率.DSP-Topk算法的裁剪处理是利用R-树中父节点空间包含子节点的思想.在DSP-Topk算法中,目标对象在插入到R-树的过程中,每个对象都对应1个节点,节点对应1个最小属性矩形(MBR).节点之间的层次关系通过矩形的包含关系来描述,对于节点有如下定义: 定义3. 最小属性矩形MBR.每个目标对象在坐标轴上的投影对应于该对象在某一个属性上的值.在二维平面内,即对象点qi在x,y轴上的投影与x,y轴构成的矩形为最小属性矩形,记为MBRi. 定义4. 属性矩形包含关系.对于qi对应的最小属性矩形MBRi和qj对应的最小属性矩形MBRj.如果S(MBRi)≥S(MBRj),且MBRj与MBRi重叠且重叠面积等于MBRj则称MBRj包含于MBRi,记为MBRj⊆MBRi. DSP-Topk的裁剪处理如图4所示,在考虑二维属性的情况下,集合Q={q1,q2,…,q10}分布在平面上且认为目标对象的属性值越小越优.对于qi所对应的MBRi来说如果MBRi包含其他对象的最小矩形,则易知该对象并非最优解,故可以舍弃,如q4对应的MBR4⊇MBR8.当MBRi不包含其他目标对象的最小矩形时,说明该对象为最优解的候选对象,如MBR2和MBR9. Fig. 4 DSP-Topk pruning processing schematic图4 DSP-Topk裁剪处理示意图 DSP-Topk算法在进行多目标优化时对于目标对象的总体评价公式为 (2) 其中,q.value[i]是记录目标对象在第i个属性上的评价值,w[i]是用户自定义的在第i个属性上的影响因子.对于目标对象中用户关心属性的评价值可参照用户自定义或者经验公式统一量化. 在障碍空间中移动对象之间的距离计算复杂性增加,对象的属性具有不确定性,所以对算法的适应性提出了更高的要求.当目标对象数量较小时,传统的多目标优化算法可以满足要求,但是目标对象集合大小超过一定量级,传统的算法就不再适用.更为重要的是已有研究中的多目标优化算法没有考虑到实际场景中移动对象属性发生变化的情况,只是针对某一时刻的静态数据进行查询.由于移动对象的属性具有不确定性,时刻t1移动对象的属性可能在时刻t2发生改变.因此为了更好地给用户提供推荐,需要在查询时考虑移动对象属性发生改变的可能.针对以上所提到的问题,提出一种改进的应用于障碍空间的多目标优化算法DSP-Topk,该算法能够高效地计算移动对象之间的最短距离,对目标对象进行预处理裁剪,并且在查询的过程中对候选集合根据目标对象属性的实际变化进行动态调整. 3.1 DSP-Topk算法的空间距离计算方法 算法1. 可视区域生成算法. 输入:查询对象p、多边形的顶点数组Obstacles; 输出:可视区域VISA(p). 子函数说明:Calc_angle(pointA, pointB)函数输入平面内2个点A,B输出A,B与x轴构成的夹角;Judge(pointA, pointB,pointC) 函数输入平面内3个点A,B,C,其中A是多边形最高点,B是多边形最低点,判断C点是否在A的上方或者B的下方,如果是,就输出true;反之,则输出false. 变量定义:顶点个数obstacles_num、顶点数组Obstacles,Angle= 180°、最佳顶点:best_A和best_B. ①max_angle←0°; ② fori←0 toobstacles_numdo ③ forj←0 toobstacles_numdo ④ ifi=jthen ⑤ continue; ⑥ else ⑦angle_a←Calc_angle(Obstacles[i],target); ⑧angle_b←Calc_angle(Obstacles[j],target); ⑨less_angle←(angle_a>angle_b?angle_a-angle_b:angle_b-angle_a); ⑩ end if 算法2. 夹角计算算法. 输入:目标对象点qi、查询对象点p; 输出:qi相对于以查询对象点p为原点与x轴构成的夹角. 变量定义:Angle=180°,PI为圆周率. ①a←0,b←0,c←0 ; ②angle←0; ③a←p1.x-p2.x; ④b←p1.y-p2.y; ⑤c←ba; ⑥angle←arctan(c)×AnglePI; ⑦ ifc≤0 then ⑧angle←angle+Angle; ⑨ else ⑩angle←angle; 根据算法1和算法2得到查询对象p的可视区域VISA(p),根据性质3将移动对象之间的最短距离计算分为2种情形:1)每个在VISA(p)中的目标对象qi与查询对象p的最短距离是二者之间的欧氏距离即mindis=|p,qi|;2)不在VISA(p)的目标对象qi,最短距离是将目标对象和查询点与多边形Si的顶点集合V构成的一张无向图G,如图5所示.根据Dijkstra算法,得出目标对象与查询对象之间的最短路径,图5中查询对象p和目标对象q之间的最短距离为mindis=|p,v2|+|v2,v3|+|v3,v4|+|v4,q|. Fig. 5 Weighted undirected graph图5 带权无向图 在顾客查询餐馆的例子中,利用算法1和算法2计算出图5中目标对象集与查询对象p的最短距离以及用户所关心的其他非空间属性如表1所示. Table 1 Target Objects Set Properties 3.2 DSP-Topk算法的裁剪操作 裁剪操作的目的是缩小目标对象集的规模,从而减少算法执行过程中所需的资源,提高算法的效率.如算法3所示:首先初始化1个队列A和1棵R-树(行①②),将每个目标对象插入到R-树;然后调整R-树(行④~⑦);最后遍历R-树,将所有的叶子节点加入到队列A中(行⑧⑨)得到最优解候选集. 算法3. DSP-Topk裁剪算法. 输入:数组tar_object; 输出:裁剪后的最优解候选集A. 变量说明: 数组tar_object为目标对象集合、tar_num为目标对象大小. ① 初始化queueA; ② 初始化R_tree; ③ 输入tar_object; ④ fori←0 totar_numdo ⑤insert(r_tree,tar_object[i]);*将移动 对象插入到R-树的叶子结点* ⑥adjust(r_tree);*调整R-树* ⑦ end for ⑧ traverse ther_treefromroot;*遍历R-树 将所有叶子结点加入到队列A中* ⑨ add allleafnodetoA; ⑩ returnA. 经过算法3裁剪过后的候选集为A={q2,q8,q9}.对于目标对象中用户关心属性的评价值参照用户自定义或者其他经验公式统一量化.最后可以将候选集归结为如表2所示: Table 2 Optimal Solution Properties of Candidates 3.3 动态调整和阈值二次裁剪 Fig. 6 Target objects dynamic change图6 目标对象动态变化示意图 由于目标对象的属性具有不确定性,所以在查询过程中当目标对象的属性发生改变时,就可能影响查询结果.如顾客查询餐馆的排队人数时,在查询的过程中,由于其他顾客的进出,导致餐馆在排队人数这个属性上发生改变.图6为目标对象属性动态变化的示意图,其中图6(a)为在3维属性空间中的目标对象动态变化情况,图6(b)为在属性1和属性2构成的平面上的投影. 在进行移动对象动态调整时,需要将动态变化的对象与参考对象ref比较支配情况.其中对于目标对象属性支配和参考对象ref有如下定义: 定义5. 目标对象属性支配.对于对象qi和qj,如果qi在某1个属性上优于qj且其他属性都不比qj差,则称qi支配qj,记为qi>qj;反之则称qi被qj支配,记为qi 定义6. 参考对象.参考对象ref属于初始候选集A且不在动态变化集D中,记为{ref|ref∈A∧ref∉D}.如果A⊆D,则说明初始候选集中的对象都发生了变化,需重新查询. 在查询过程中目标对象的某些属性实时发生了改变.为了准确地反映目标对象的真实情况需要对动态变化情况进行考虑.DSP-Topk算法中目标对象集合经过裁剪已经生成1个候选集A,此时需要将A与动态变化的集合D进行比较. 算法4. DSP-Topk动态调整算法. 输入:候选集数组SP、动态变化集数组c_object、动态调整参考对象ref; 输出:调整后的候选集A′. 变量说明:judge_num发生变化的移动对象个数;c_object[judge_num]发生变化的移动对象集合;sp_num原最优解候选集个数;SP[sp_num]初始候选集. ①flag←0; ② fori←0 tojudge_numdo ③ forj←0 tosp_numdo ④ ifc_object[i].num=SP[j].numthen*动态变化的对象是初始候选集中 对象* ⑤flag←1; ⑥ 比较c_object[i]和ref; ⑦ ifc_object[i]不被ref支配 then*变化的对象不被ref支配,则 更新对象信息* ⑧SP[j]←c_object[i]; ⑩ ifj=sp_num-1 then 阈值二次裁剪是针对用户在某些属性上提出的最低接受条件,阈值的提出意味着某1个目标对象即使在某些属性上绝对的占优,但是如果不满足阈值条件那么它也不会成为最优解. DSP-Topk算法在目标对象经过动态调整后进行阈值二次裁剪.如顾客找餐馆的例子,经过动态调整后的最优解候选集为D={q2,q11,q9}.如果顾客在餐馆价格优惠上提出阈值条件至少打8折,那么经过阈值二次裁剪后得到新的最优解候选集为如表3所示: Table 3 Optimal Solution Properties of Candidates 对于动态调整和阈值二次裁剪后的候选集,利用式(2)对每个候选对象进行总体评价求和.总体评价后需要将候选集中所有对象排序.其中DSP-Topk算法中采用堆排序中的小顶堆排序.排序过程中,首先初始化1个小顶堆;然后将每个候选对象插入到堆中,调整堆的顺序;最后得到1个包含所有候选对象的小顶堆.其中小顶堆内父节点的值不大于子节点,所以根节点是整个堆中的最小值,即用户所关心的最佳选择对象.在顾客找餐馆的例子中经过DSP-Topk算法后所得到的最佳选择对象为q10={10,8.0,5}. 为了验证DSP-Topk算法的可行性和有效性,对其进行了实验测试.实验所采用的数据为综合商场真实的商品信息数据,其中商品大类有1 403类,商品种类总数是66 231个,测试数据来源于国内首家大数据交易平台数据堂.其中顾客、商场障碍物和商品空间分布则随机生成在商场二维平面图上,平面图大小为500×500个单位坐标.根据DSP-Topk算法,首先通过商品的空间分布利用可视区域算法得到商品与顾客之间的最短距离;然后加上顾客关心的非空间属性如(价格、销售情况和折扣等)进行多目标优化查询.实验测试了不同条件下DSP-Topk算法与已有多目标优化算法(Topk和DS-Topk)在查询性能上的差异.为避免随机性,查询时间取10次测试的平均时间.实验中的目标属性和阈值均由用户的查询提出和确定.其中为了验证DSP-Topk算法中动态调整的有效性,实验过程中手动对顾客的空间位置和商品的某些属性进行动态修改,如价格和折扣等. 4.1 静态场景下DSP-Topk算法查询性能分析 图7所示为静态状态下目标对象集合大小对查询性能的影响.从图7中可以看出:当目标对象集合较小时,DSP-Topk算法所耗费的时间要大于已有的多目标优化算法.主要原因是DSP-Topk算法需要对目标对象进行裁剪、动态变化判断等步骤花费了一部分时间.但是,随着目标对象集合的增大,DSP-Topk算法的优越性就可以逐步体现.因为已有的多目标优化算法需要对所有的目标对象进行遍历,查询时间与目标对象的个数成正比.DS-Topk相比于Topk在最终对目标对象进行排序选择时,对排序算法进行了优化所以DS-Topk的效率优于Topk.由于DSP-Topk算法先对目标对象集合进行一遍裁剪,删除了绝大部分候选目标,得到1个数量比原先小得多的最优解候选集.这种执行机制保证了DSP-Topk算法与目标对象的个数关系无正相关性,随着目标对象个数的增加,执行时间增加幅度趋于平缓. Fig. 7 Impact of size of the static target set on query performance图7 静态目标对象集的大小对查询性能的影响 4.2 动态场景下DSP-Topk算法查询性能分析 已有的多目标优化算法没有考虑目标对象的属性发生动态变化的情况,当目标对象的属性值发生改变时,有可能对最终的查询结果产生影响.为了保证查询结果的准确性,传统算法就需要多次查询,而DSP-Topk算法在执行过程中考虑到目标对象属性发生动态变化的情况.如图8所示为动态变化情况下目标对象集合大小对查询性能的影响.对比图7在目标对象集合较小时,DSP-Topk由于步骤较多执行时间会多于传统算法;但动态变化情况下,已有算法由于要多次查询导致时间增加,故DSP-Topk算法查询时间始终优于已有算法. Fig. 8 Impact of size of the dynamic target set on query performance图8 动态变化下目标对象集合大小对查询性能的影响 4.3 目标对象属性个数对查询性能的影响 对于同一个目标对象,不同的用户所关心的属性类型和个数是不一样的.图9为对象集合规模为10 000时,目标对象的属性个数对查询性能的影响,从图9中可以看出已有的多目标优化算法随着目标对象属性个数的增加,查询时间呈线性增长,这是因为已有算法的时间消耗基本在累加计算上,在进行目标对象总体评价时需要对所有属性进行累加计算,因此属性个数的增加导致查询时间的增加.而DSP-Topk算法消耗的大部分时间在目标对象动态调整上,对于目标对象属性个数的增加只影响在目标对象裁剪过程中,而且裁剪过程中进行目标对象比较时只需判断大小而不需要累加计算,所以属性个数的增加对DSP-Topk 算法的查询效率影响不大. Fig. 9 Number of attributes to query performance图9 属性个数对查询性能的影响 4.4 目标对象动态变化集合规模对查询性能的影响 DSP-Topk算法需要将动态变化的集合D与裁剪得到初始候选集SP进行比较得到新的候选集,因此动态变化集合D的大小直接影响查询效率.为了更好地反映动态变化集合规模对查询性能的影响,实验测试了不同动态变化比例下DSP-Topk和传统Topk算法查询性能变化的情况,如图10所示,随着目标对象动态变化集合比例的增加,已有算法查询性能变化不大,这是由于已有多目标优化算法通过连续查询和遍历全部目标对象的机制来适应目标对象属性发生动态变化的情况;DSP-Topk算法随着目标对象动态变化集合比例的增加,查询时间也随之增加,当动态变化的比例增加到50%左右时,DSP-Topk算法的查询时间增速出现明显的提升.实验还发现对于不同的查询规模,增长点基本在50%~60%之间浮动,此时最优解候选集的规模占总体查询规模的1%左右.如图10所示,当测试规模达到10 000时,增速提升发生在55%左右,最优解候选集的个数约为100;当测试规模为20 000时,增速提升发生在50%左右,最优解候选集的个数约为200. Fig. 10 Dynamic changing scale to query performance图10 动态变化规模对查询性能的影响 4.5 目标对象动态变化规模对候选集的影响分析 目标对象属性动态变化对最优解候选集的影响分为3种情况:1)原先在候选集中的对象发生改变,但改变后的对象仍然是最优解的候选对象,此时更新目标对象记为update_sp;2)原先在候选集中的对象发生改变后不再是最优解的候选对象,此时从初始候选集中删除对象记为del_sp;3)原先不在候选集中的对象发生改变后成为最优解的候选对象,此时需要将该对象加入到候选集中记为add_sp.如图11所示,当目标对象动态变化的比例增加,这三者的规模同时增加,但是add_sp增速和比重远大于前2种.如图11(b)的扇形图可以发现,add_sp的比例达到23左右.因此可以得出这样的结论:目标对象属性动态变化对于初始候选集的影响主要归结于原先不在候选集中的目标对象,经动态变化后成为了最优解的候选对象. Fig. 11 Dynamic changing scale to candidate set图11 动态变化规模对候选集的影响 在障碍空间中提出一种支持目标对象属性动态调整的多目标优化算法DSP-Topk.算法面向具有多属性的目标对象,采用预处理的裁剪策略降低目标对象集合规模.在查询过程中,移动对象之间的互相影响可能会改变目标对象属性,导致目标对象属性具有不确定性.DSP-Topk算法引入目标对象动态调整机制,提出动态集和静态集的概念,当目标对象属性发生改变时,只需针对动态集和候选集进行比较并生成最终结果,提高了算法的效率.通过实验对DSP-Topk算法和已有的移动对象多目标优化算法在多种条件下进行了对比和分析.实验结果表明:DSP-Topk算法在目标对象集合较大时,更能体现其在查询性能上的优势.动态规模改变对查询性能和候选集的影响也通过实验进行了分析,发现目标对象动态比例与查询时间成正相关变化,其中新增候选对象对候选集的影响最大.此外,已有的移动对象多目标优化算法对用户关心的属性个数十分敏感,查询时间与属性个数成线性增长.但属性个数的增加对DSP-Topk算法查询性能影响不大,随着属性个数的增加,算法仍然具有较好的查询性能. [1]Zhou Aoying, Yang Bin, Jin Cheqing, et al. Location-based services: Architecture and progress[J]. Chinese Journal of Computers, 2011, 34(7): 1155-1171 (in Chinese)(周傲英, 杨彬, 金澈清, 等. 基于位置的服务: 架构与进展 [J]. 计算机学报, 2011, 34(7): 1155-1171) [2]Meng Xiaofeng, Chen Jidong. Moving Objects Management[M]. Berlin: Springer, 2010: 120-135 [3]Soliman M A, Ilyas I F, Chen-Chuan C K. Top-kquery processing in uncertain databases[C]Proc of the 23rd IEEE Int Conf on Data Engineering (ICDE). Piscataway, NJ: IEEE, 2007: 896-905 [4]Borzonyi S, Kossmann D, Stocker K. The skyline operator[C]Proc of the 17th IEEE Int Conf on Data Engineering (ICDE). Piscataway, NJ: IEEE, 2001: 421-430 [5]Kossmann D, Ramsak F, Rost S. Shooting stars in the sky: An online algorithm for skyline queries[C]Proc of the 28th Int Conf on Very Large Data Bases (VLDB). San Francisco: Morgan Kaufmann, 2002: 275-296 [6]Wu Wei, Guo Wenyuan, Tan K-L. Distributed processing of movingk-nearest-neighbor query on moving objects[C]Proc of the 23rd IEEE Int Conf on Data Engineering (ICDE). Piscataway, NJ: IEEE, 2007: 1116-1125 [7]Deb K. Multi-objective optimization using evolutionary algorithms[J]. Computer-Aided Civil and Infrastructure Engineering, 2001, 2(3): 509-521 [8]Xu Jianqiu, Güting R H, Qin Xiaolin. GMOBench: Benchmarking generic moving objects[J]. GeoInformatica, 2014, 19(2): 227-276 [9]Güting R H, Almeida V T, Ding Zhiming. Modeling and querying moving objects in networks[J]. The International Journal on Very Large Data Bases, 2006, 15(2): 165-190 [10]Jin Peiquan, Wang Na, Zhang Xiaoxiang, et al. Moving object data management for indoor spaces[J]. Chinese Journal of Computers, 2015, 38(9): 1777-1795 (in Chinese)(金培权, 汪娜, 张晓翔, 等. 面向室内空间的移动对象数据管理[J]. 计算机学报, 2015, 38(9): 1777-1795) [11]Yuan Wenjie, Schneider M. Supporting continuous range queries in indoor space[C]Proc of the 11th Int Conf on Mobile Data Management. Piscataway, NJ: IEEE, 2010: 209-214 [12]Lee J. A spatial access-oriented implementation of a 3-D gis topological data model for urban entities[J]. GeoInformatica, 2004, 8(3): 237-264 [13]Lu Hua, Cao Xin, Jensen C S. A foundation for efficient indoor distance-aware query processing[C]Proc of the 28th IEEE Int Conf on Data Engineering (ICDE). Piscataway, NJ: IEEE, 2012: 438-449 [14]Xu Hu, Li Zhicheng, Lu Yansheng, et al. Group Visible Nearest Neighbor Queries in Spatial Databases[M]. Berlin: Springer, 2010: 333-344 [15]Gu Yu, Yu Xiaonan, Yu Ge. Method for continuous reversek-nearest neighbor queries in obstructed spatial databases[J]. Journal of Software, 2014, 25(8): 1806-1816 (in Chinese)(谷峪, 于晓楠, 于戈. 一种障碍空间数据库中的连续反k近邻查询方法[J]. 软件学报, 2014, 25(8): 1806-1816) [16]Nutanong S, Zhang Rui, Tanin E, et al. The V*-Diagram: A query dependent approach to moving knn queries[J]. Proceedings of the VLDB Endowment, 2008, 1(1): 1095-1106 [17]Gao Yunjun, Zheng Baohua, Chen Gencai, et al. Visible reversek-nearest neighbor query processing in spatial databases[J]. IEEE Trans on Knowledge and Data Engineering, 2009, 21(9): 1314-1327 [18]Nutanong S, Tanin E, Zhang Rui. Visible Nearest Neighbor Queries[M]. Berlin: Springer, 2007: 876-883 [19]Freitas A A. A critical review of multi-objective optimization in data mining [J]. ACM SIGKDD Explorations Newsletter, 2004, 6(2): 77-86 [20]Wei Xiaojuan, Yang Jing,Li Cuiping, et al. Skyline query processing[J]. Journal of Software, 2008, 19(6):1386-1400 (in Chinese)(魏小娟, 杨婧, 李翠平, 等. Skyline查询处理[J]. 软件学报, 2008, 19(6): 1386-1400) [21]Papadias D, Tao Yufei, Fu G, et al. An optimal and progressive algorithm for skyline queries[C]Proc of the 2003 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2003: 467-478 [22]Papadias D, Tao Yufei, Fu G, et al. Progressive skyline computation in database system[J]. ACM Trans on Database System, 2005, 30(1): 41-82 [23]Yin Jian, Yao Shuyu, Xue Shao’e, et al. An index based efficientk-dominant skyline algorithm[J]. Chinese Journal of Computers, 2010, 33(7): 1236-1245 (in Chinese)(印鉴, 姚树宇, 薛少锷, 等. 一种基于索引的高效k-支配Skyline算法[J]. 计算机学报, 2010, 33(7): 1236-1245) [24]Zhang Bin, Jiang Tao, Gao Yunjun, et al. Topkquery processing of reverse skyline in metric space[J]. Journal of Computer Research and Development, 2014, 51(3): 627-636 (in Chinese)(张彬, 蒋涛, 高云君, 等. 度量空间中的Topk反向Skyline查询算法[J]. 计算机研究与发展, 2014, 51(3): 627-636) [25]Jiang Tao, Zhang Bin, Gao Yunjun, et al. Efficient Topkquery processing on mutual skyline[J]. Journal of Computer Research and Development, 2013, 50(5): 986-997 (in Chinese)(蒋涛, 张彬, 高云君, 等. 高效的Topk相互Skyline查询算法[J]. 计算机研究与发展, 2013, 50(5): 986-997) Li Bohan, born in 1979. PhD. Associate professor of Nanjing University of Aeronautics and Astronautics. Member of CCF. His main research interests include spatial and spatio-temporal databases and geographic information system. Zhang Chao, born in 1991. Master candidate of Nanjing University of Aeronautics and Astronautics. Student member of CCF. His main research interests include spatio-temporal databases and uncertain moving objects indexing technology (zhangchao0607@nuaa.edu.cn). Li Dongjing, born in 1991. Master candidate of Nanjing University of Aeronautics and Astronautics. Student member of CCF. Her main research interests include spatio-temporal databases and uncertain moving objects indexing technology ( 960395655@qq.com). Xu Jianqiu, born in 1982. PhD. Associate professor of Nanjing University of Aeronautics and Astronautics. Member of CCF. His mian research interests include spatio-temporal databases and moving objects indexing technology (jianqiu@nuaa.edu.cn). Xia Bin, born in 1992. Master candidate of Nanjing University of Aeronautics and Astronautics. Student member of CCF. His main research interests include spatio-temporal databases and security in distributed environment(742724470@qq.com). Qin Xiaolin, born in 1953. PhD. Professor of Nanjing University of Aeronautics and Astronautics. Senior member of CCF. His main research interests include spatio-temporal databases and security in distributed environment( qinxcs@nuaa.edu.cn). A DSP-Topk Query Optimization Algorithm Supporting Indoor Obstacle Space Li Bohan1,2,3, Zhang Chao1, Li Dongjing1, Xu Jianqiu1,2, Xia Bin1, and Qin Xiaolin1,2 1(SchoolofComputerScienceandTechnology,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016)2(CollaborativeInnovationCenterforNovelSoftwareTechnologyandIndustrializationofJiangsuProvince,Nanjing210016)3(JiangsuEasymapGeographicInformationTechnologyCorpLtd,Yangzhou,Jiangsu225000) Multi-objective optimization is one of the key technologies in moving objects data management. While in the procession of multi-objective optimization query, the concerned target object’s attributes may depend on the other moving objects’ attributes. Therefore, moving objects can affect each other, which will lead to the uncertainty of the object’s properties. The existing multi-objective optimization algorithms need to traverse all the target objects, furthermore, they can’t effectively solve the problem of dynamic change of object attributes. We propose an effective multi-objective optimization algorithm DSP-Topk (dynamic and support pruning Topk) to solve the query in the obstacle space. Visual area model can calculate the distance between the moving objects with obstacles. The method of viewable area which applies the maximum differential angle can improve the calculation performance of the distance between moving objects. Then, we study the uncertainty of the object’s attributes by using the dynamic adjustment mechanism. The given pruning strategy with preprocessing improves the efficiency of the query. The results of experiments indicate that DSP-Topk algorithm improves the query efficiency significantly compared with the existing Topk algorithm and DS-Topk algorithm. Combined with the real testing data of goods in stores, the rationality and effectiveness of the algorithm are also verified. moving objects; multi-objective optimization; uncertainty; pruning; dynamic adjustment 2015-10-09; 2016-02-16 国家自然科学基金项目(61373015,61300052,41301047);中央高校基本科研业务费专项资金项目(NP2013307, NZ2013306); 中国留学基金委国家公派留学项目(201406835051); 中国民用航空局安全能力建设基金(AS-SA201521);江苏省自然科学基金青年基金项目(BK20130819);江苏高校优势学科建设工程资助项目;南京航空航天大学科研基地创新基金(NJ20160028);南京航空航天大学研究生创新实验室开放基金项目(kfjj20151607). This work was supported by the National Natural Foundation of China(61373015,61300052,41301047), the Fundamental Research Funds for the Central Universities (NP2013307, NZ2013306), the China Scholarship Council Study Abroad Program (201406835051), the Funding of Security Ability Construction of Civil Aviation Administration of China (AS-SA201521), the Natural Science Foundation of Jiangsu Province for Youth Scholars (BK20130819), the Project Funded by the Priority Academic Program Development of Jiangsu Province Higher Education Institutions, the Innovation Funding of Nanjing University of Aeronautics and Astronautics (NJ20160028), and the Graduate Innovation and Practice Foundation of Nanjing University of Aeronautics and Astronautics (kfjj20151607). TP311



3 支持裁剪和动态调整的DSP-Topk算法



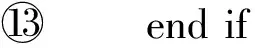


































4 实验与结果分析


5 结束语







