基于分组策略的补货配送问题优化模型*
刘艳秋, 曹 歌, 张 颖, 李 佳
(沈阳工业大学 a.理学院, b.信息科学与工程学院, 沈阳 110870)
信息科学与工程
基于分组策略的补货配送问题优化模型*
刘艳秋a, 曹 歌a, 张 颖a, 李 佳b
(沈阳工业大学 a.理学院, b.信息科学与工程学院, 沈阳 110870)
针对已存在的供应链环境下较少考虑补货配送问题中的分组配送策略,结合大量零售商对单一产品需求量不同等特点,引入分组的决策变量.根据配送中心补货周期与配送次数的函数关系,以最小化三级供应链系统的平均总成本为目标,构建了带有配送中心能力约束的补货配送优化模型.根据优化模型的特点,利用改进的遗传算法求解模型,并进行了数据仿真试验.结果表明,该优化模型能为配送中心提供一种有效的分组配送方案,选择的优化算法更稳定快捷,能为企业提供有益的管理启迪.
物流;供应链;配送中心;补货配送优化模型;补货周期;配送次数;分组策略;遗传算法
供应链是产品由生产端传送到客户端过程中所历经的各个环节,是由企业共同构建的链状网络.配送中心作为供应链中连接上游供应方和下游需求方的关键一环,对整个供应链的管理有着重要影响.其中,配送中心涉及的补货与配送问题是影响其发展的两个关键问题.由于在补货与配送问题中考虑的库存与运输成本存在着一种此盈彼亏现象,因此在研究中常将二者联合探讨,益于供应链系统的集成决策,实现配送中心资源配置与客户需求的高度结合,提高客户服务水平.
目前,研究供应链中补货配送问题的文献有很多.在研究此问题时,大多数文献采用整数比周期策略和二次幂周期策略等补货策略进行补货[1-2],以补货和配送相关总成本为目标函数[3-4],并建立数学模型,利用差分进化算法和遗传算法等优化算法来求解模型[5-7].闵杰等[8]将变质性商品的需求量伴随库存的变化而变化这一特点考虑到补货配送问题中,从而使构建的模型更符合实际需要;林峰等[9]以易腐品为研究对象,将时间、载重成本等因素引入到模型中,构建了基于需求分割配送决策下的补货配送优化模型;刘玉伟等[10]建立补货配送模型时考虑了分组配送策略,从而优化了总成本.在现有补货配送问题的研究中忽略了物流的具体配送过程,常默认为运输车辆依次或一对一地为零售商进行送货,在针对大量异质零售商环境下,采用这两种方法送货耗时长、成本高且会耽误零售商的正常运营,因此需要在物流配送过程中引入分组配送策略.文献[10]虽然考虑了分组配送,但其直接给定了分组数和组与组之间配送周期关系,文献[10]的分组决策仍具有局限性.
本文研究了在确定需求下零售业配送中心单一产品补货与配送联合优化问题,在研究此问题中引入了分组的决策变量,通过采用分组策略有效改善物流配送过程,制定出配送中心最佳的补货周期和每组配送次数,合理分配配送中心资源并选择优化的路径进行配送,从整体上协调供应链管理,增加企业的竞争力.模型涉及到三个决策变量,可能会造成求解复杂解空间的问题,本文在求解时先进行降维处理,再利用遗传算法进行运算.
1 补货配送优化模型
1.1 问题描述
考虑由一个供应商、一个配送中心、多个零售商组成的三级供应链系统(简称1-1-N系统).供应商负责提供单一产品,配送中心在一定周期内对自身进行补货,并且配送中心根据汇总的各零售商提供的补货产品信息为各零售商制定配送策略.该供应链中系统产生的成本主要有配送中心的订货成本、库存成本和配送成本,以及零售商的库存成本.目标是以最小化系统平均总成本来制定配送中心补货策略和配送策略,使配送中心资源得到合理利用.供应链物流网络结构如图1所示.
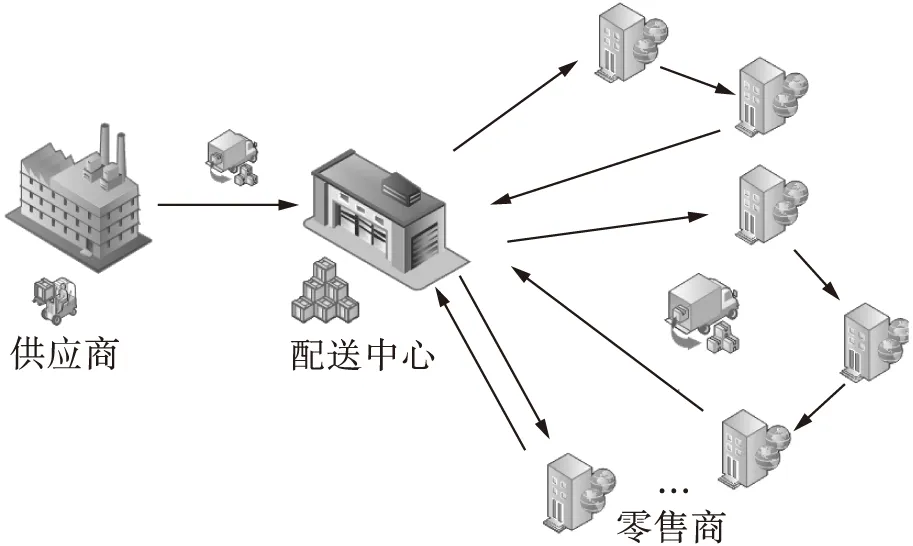
图1 供应链物流网络结构Fig.1 Structure of supply chain logistics network
1.2 变量描述及条件假设
在建模过程中涉及到的变量分别为:N为零售商的集合;I为零售商分组的集合;S为配送中心的固定订货成本;C0为配送中心单位货物的存储费;C1为零售商单位货物的存储费;C2为单位距离车辆运输费;rij为第i组中第j个零售商每天的需求量;Q1为配送中心单位车辆的最大载重量;y为配送中心在此种产品上可供调配的最大车辆数;D为配送中心单位车辆的最大行驶距离;di(j-1),ij为第i组中第j-1个零售商到第j个零售商的距离(其中,di0,ij为配送中心到第j个零售商的距离).决策变量分别为:T为配送中心的补货周期;pi为配送中心在补货周期内为第i组零售商进行配送的次数,同一组的零售商配送次数相同,不同组的零售商配送次数互不影响,其值取整数;xij为选择为第i组中第j个零售商配送时其值为1,否则为0.
模型的建立基于以下假设:1)配送中心的补货提前期很短,可以忽略不计;2)在此三级供应链中只考虑对单一产品进行补货,且不出现送货延迟或缺货情况;3)每条线路上只需一辆车进行配送,每个零售商只允许出现在一条线路上;4)零售商每天的需求量是连续均匀的,且需求量确定.
1.3 模型建立
在由一个供应商、一个配送中心、多个零售商组成的三级供应链中,配送中心产生的物流费用主要包括订货成本、库存成本和配送成本,其中,订货成本和库存成本为
(1)
配送成本主要是车辆行驶费,即
(2)
零售商产生的物流费用主要是库存成本,即
(3)
综合配送中心订货成本、库存成本和配送成本,以及零售商的库存成本,三级供应链系统的单位时间总成本为
(4)
建立配送中心补货配送联合优化模型,其表达式为
(5)
s.t.
(6)
(7)
(8)
(9)
(10)
xij=0,1 ∀i∈I,j∈N
(11)
其中,补货配送优化模型的目标函数式(5)为三级供应链系统产生的单位时间物流总成本,包括配送中心的订货成本、库存成本和配送成本,以及零售商的库存成本;式(6)表示时间约束,即配送中心的配送周期要比配送中心的补货周期小;式(7)表示第i组中的零售商配送时的行驶距离不能超过车辆的最大行驶距离;式(8)表示第i组中零售商配送时的配送量不能超过单位车辆的最大载重量;式(9)表示配送中心每次订货总量不能超过配送中心的最大服务能力;式(10)限制每个零售商只能出现在一个分组中;式(11)为变量约束,即0-1变量.
2 算法设计
2.1 最佳补货周期
根据补货配送模型中的目标函数可得
(12)

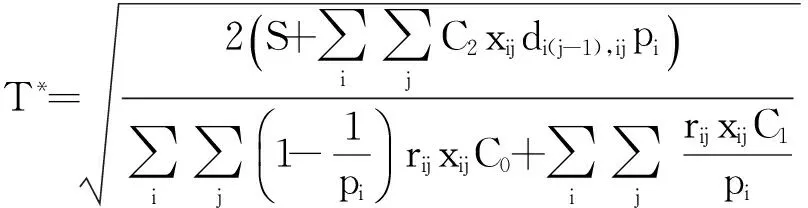
(13)
2.2 改进的遗传算法
本文研究的补货配送联合优化问题是强NP问题,现有文献对此类问题多采用智能优化算法进行求解.本文提出的补货配送优化模型求解的难度是考虑零售商的不同分组和每组配送次数的选择,在进行划分时会受到零售商需求量、车辆的载重量和行驶距离等因素的影响,并且在优化模型中将会遇到复杂的求解空间问题.综合以上考虑,本文选取遗传算法并结合自身模型特点对其进行改进来求解模型.遗传算法具体操作流程如下:
1) 初始化种群与染色体编码.设置初始时刻t=0,种群规模NP=100,最大遗传代数NG=200.染色体编码使用二进制遗传编码[11],采用以零售商为基因、零售商的组号xij和每组的配送次数值pi为基因值的编码方式,xij取值为1或0,pi取值上限为10.
2) 适应度计算.模型中目标函数为求最小值问题,在运算时转化为求目标函数的最大值.
3) 选择操作.采用轮盘赌选择法[12],选择适应性较高的个体作为优秀个体进行遗传,适应性较高的个体得到的繁殖机率较大.
4) 交叉与变异.采用双切点交叉操作,设置交叉概率Pc=0.9;变异则是选取种群中个体的某些基因位值,并将选取的位值进行变化,设变异概率Pm=0.08.
5) 判断停止条件.若最大遗传代数达到200,则停止计算,输出最优解.
3 仿真试验与对比分析
在由一个供应商、一个配送中心和8个零售商组成的三级供应链算例中,供应商提供单一产品,配送中心的固定订货成本为200元,车辆行驶单位距离的运输费为0.5元/km,每辆车载重3t,配送中心有5辆车可供调配,车辆的最大行驶距离为1 000km,零售商、配送中心的数据以及节点间距如表1、2所示.
表3为不同分组下的配送中心最佳决策.由表3可知,当配送中心分2组进行配送时,配送中心最佳补货周期为5.782 6d,零售商5为一组在补货周期内配送一次,零售商1、2、3、4、6、7、8为一组在补货周期内配送两次,此时的系统平均总成本为190.40元;当配送中心分3组进行配送时,配送中心最佳补货周期为5.821 6d,零售商1、2、4为一组在补货周期内配送一次,零售商3、6、7为一组在补货周期内配送两次,零售商5、8为一组在补货周期内配送一次,所得到的系统平均总成本为219.19元.通过对比可以发现,分2组时系统平均总成本最小,因此,配送中心在为零售商进行配送时分2组更好.
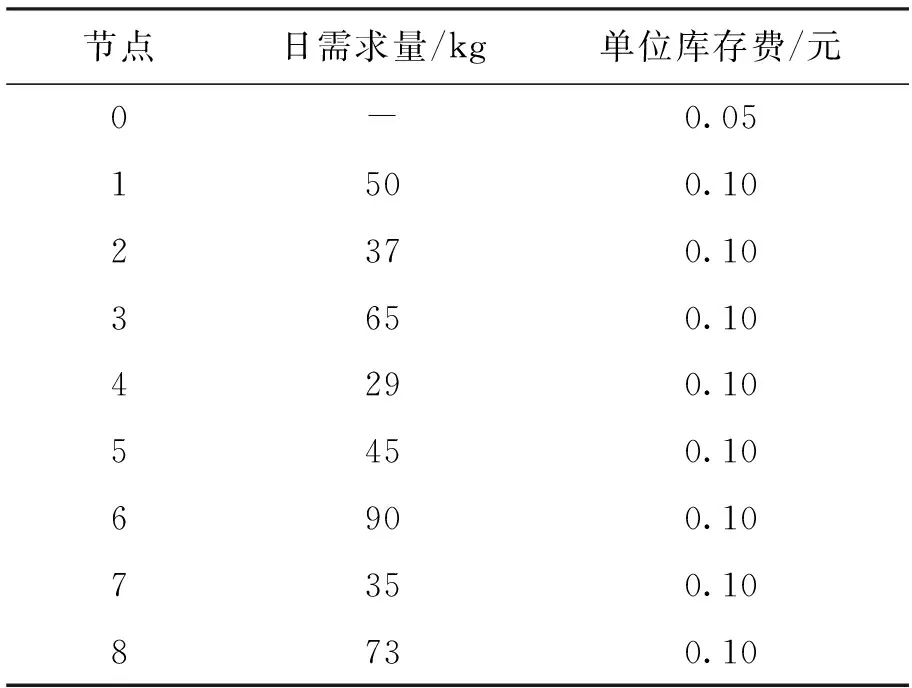
表1 零售商参数Tab.1 Parameters for retailers
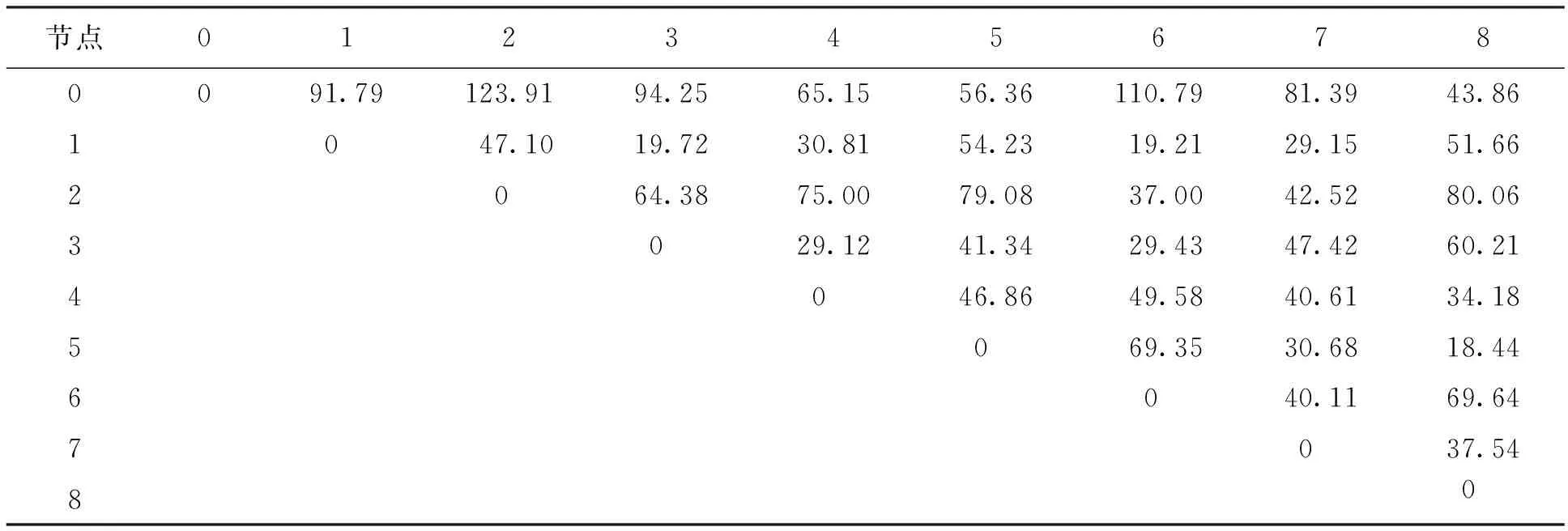
表2 配送中心和零售商节点间距Tab.2 Node distances between distribution centers and retailers km

表3 不同分组下的配送中心最佳决策Tab.3 Optimal decisions of distribution center under different grouping conditions
表4给出了采用文献[10]中的分组策略与本文中的分组策略进行对比的结果,可以发现本文中的分组策略较优,使得系统平均总成本更小.
4 结 论
配送中心科学地进行补货与配送可以有效提高企业的效率,减少企业成本,因而补货与配送问题也逐渐引起人们的重视,其研究也更具有学术价值.对于配送中心来说,采取何种补货策略与配送策略是解决问题的重点.本文在设计模型时考虑到灵活分组因素,以优化配送中心的订货成本、库存成本和配送成本,以及零售商的库存成本为目标,建立更贴近实际需求的配送中心补货配送优化模型,其结果证实了该模型的有效性,采用的分组配送策略能使企业达到节约成本的目的,并促进企业快速整合内部资源来响应客户需求,提升企业的服务质量.

表4 分组策略比较Tab.4 Comparison in grouping strategies
注:*表示采用文献[10]中的分组策略.

(FU Cheng-hong,FU Zhuo.A combined strategy of fixed-partition and integer-ratio for inventory routing problem [J].Journal of Railway Science and Engineering,2013,10(6):103-108.)
[2]李莉英,王勇,杨金.一类多对多物流系统的运送频率选择优化问题研究 [J].运筹与管理,2012,21(2):92-99.
(LI Li-ying,WANG Yong,YANG Jin.Shipping frequencies selection in a many-to-many logistics system [J].Operations Research and Management Science,2012,21(2):92-99.)

(ZHAO Da,LI Jun,MA Dan-xiang,et al.Optimal strategy of stochastic demand inventory routing problem and algorithms [J].Journal of Management Sciences in China,2014,17(5):14-24.)
[4]Abdul-Jalbar B,Segerstedt A,Sicilia J,et al.A new heuristic to solve the one-warehouse N-retailer problem [J].Computers and Operations Research,2010,37(2):265-272.

(WANG Lin,DUN Cai-xia,ZHANG Jin-long.Integrated joint replenishment and distribution model using hybrid differential evolution algorithm [J].Chinese Journal of Management Science,2012,20(3):86-93.)
[6]Cha B C,Moon I K,Park J H.The joint replenishment and delivery scheduling of the one-warehouse,n-retailer system [J].Transportation Research Part E,2008,44(5):720-730.
[7]Li J X,Chu F,Chen H X.A solution approach to the inventory routing problem in a three-level distribution system [J].European Journal of Operational Research,2011,210(3):736-744.

(MIN Jie,FU Juan,OU Jian,et al.An optimal inventory-distribution model with deteriorating items and inventory-level-dependent demand [J].Industrial Engineering Journal,2014,17(6):54-61.)
[9]林峰,贾涛,高艳,等.考虑分割配送的易腐品一体化库存路径问题 [J].工业工程与管理,2015,20(5):45-53.
(LIN Feng,JIA Tao,GAO Yan,et al.Integrated inventory routing problem with split-delivery for deteriorating items [J].Industrial Engineering and Management,2015,20(5):45-53.)

(LIU Yu-wei,JIA Tao,GAO Yan.The integrated production-distribution inventory model considering grouping strategy in the supply chain [J].Industrial Engineering and Management,2015,20(2):7-15.)
[11]刘艳秋,焦妮,张义华.基于低碳理念的多级物流网络优化设计 [J].沈阳工业大学学报,2015,37(4):404-409.
(LIU Yan-qiu,JIAO Ni,ZHANG Yi-hua.Optimization design for multi-level logistics network based on low carbon concept [J].Journal of Shenyang University of Technology,2015,37(4):404-409.)
[12]李志,周愉峰.考虑中断风险与库存成本的分销网络设计模型 [J].运筹与管理,2014,23(6):136-143.
(LI Zhi,ZHOU Yu-feng.Distribution network design problem considering inventory cost under the risk of disruptions [J].Operations Research and Management Science,2014,23(6):136-143.)
(责任编辑:钟 媛 英文审校:尹淑英)
Optimization model for replenishment and distribution problems based on grouping strategy
LIU Yan-qiua,CAO Gea,ZHANG Yinga,LI Jiab
(a.School of Science,b.School of Information Science and Engineering,Shenyang University of Technology,Shenyang 110870,China)
Aiming at the fact that the grouping distribution strategy in the replenishment and distribution problems is not fully considered in the existing supply chain,a decision variable for grouping was introduced in combination with such features that a large number of retailers have different demands on a single product.According to the function relationship between the replenishment cycle and delivery times,the average total cost of a minimized three-level supply chain system was taken as the objective,and the optimization model for the replenishment and distribution with the capacity constraints of distribution center was established.According to the characteristics of this optimization model,the improved genetic algorithm was used to solve the model,and the numerical simulation test was carried out.The results show that the proposed optimization model can provide an effective grouping strategy for the distribution center,and the selected optimization algorithm is more stable and rapid,which can provide the beneficial management enlightenment for companies.
logistics;supply chain;distribution center;replenishment and distribution optimization model;replenishment cycle;delivery time;grouping strategy;genetic algorithm
2016-08-31.
国家自然科学基金资助项目(70431003);沈阳市科学技术计划项目(F14-231-1-24).
刘艳秋(1963-),男,吉林四平人,教授,博士生导师,主要从事复杂系统可靠性建模与优化等方面的研究.
19 18∶00在中国知网优先数字出版.
http:∥www.cnki.net/kcms/detail/21.1189.T.20170119.1800.022.html
10.7688/j.issn.1000-1646.2017.02.09
TP 301
A
1000-1646(2017)02-0165-05

