结合稳健估计和Meanshift的视频目标跟踪算法*

朱闻亚

(1.武汉大学 经济与管理学院， 武汉 430072；2.义乌工商职业技术学院 机电信息学院， 浙江 义乌 322099)

结合稳健估计和Meanshift的视频目标跟踪算法*

朱闻亚1，2

(1.武汉大学 经济与管理学院， 武汉 430072；2.义乌工商职业技术学院 机电信息学院， 浙江 义乌 322099)

针对Meanshift目标跟踪算法对强噪声环境敏感的问题，提出了一种结合稳健估计和传统Meanshift的修正Meanshift算法.通过稳健估计修正传统Meanshift算法的核概率密度函数，提升Meanshift算法的鲁棒性.针对信噪比分别为60、30和0 db的仿真数据，将传统Meanshift算法和修正Meanshift算法的跟踪轨迹准确性和精度进行对比.结果表明，修正Meanshift算法能够实现目标准确跟踪，且跟踪位置的相对误差在1%以下.对于实际运动目标视频数据，所提算法也可以实现实时跟踪定位，克服了传统Meanshift算法目标跟踪丢失的问题.

稳健估计；均值偏移；目标追踪；噪声；核概率密度函数；中位数；误差；视频

视频目标跟踪是计算机视觉领域的常规问题，通过设计软件系统可以实现对视频内特定目标的定位和跟踪.但在实际的使用过程中，因为检测环境场景复杂及视频采集设备的移动，容易使得获取的视频数据存在大量干扰噪声，这些不必要的信息直接影响了目标检测的准确性，使得跟踪任务失败[1-5].

基于Meanshift的视频目标跟踪算法可通过设计核函数的方式，更有效地提取出表征目标的特征概率密度函数，是目前视频跟踪算法领域的主要研究对象，并衍生了多种改进算法.例如通过将检测目标的边缘特征融合，从而提高检测准确性[6]；或是对检测目标图像进行分块，然后对每个分块施加更具有针对性的核函数[7]；亦或采用多尺度联合的方式将不同层次的目标特征进行加权组合，从而实现高效跟踪，并且可与卡尔曼滤波、粒子滤波等方法进行融合来进行目标追踪[8-9].这些方法虽提升了目标跟踪的效率和准确性，却仅单一考虑了目标的特征，研究主要着力点均是增强目标特征的提取，却忽视了背景对目标特征的影响.尽管核函数本身可有效地将目标以外的视频像素点的灰度信息进行抑制，但对于存在目标内的噪声、背景干扰以及目标外的强噪声干扰却鲜有帮助.显然，只有对噪声、干扰以及目标的统计特性进行合适地估计，并针对性设计抑制噪声的算法才能更有效地解决上述问题[8-13].

本文提出一种结合稳健估计和Meanshift的目标追踪算法，通过稳健估计设计鲁棒性更强的核函数，从而提升Meanshift算法检测的准确性，保证其在强噪声背景下也能准确识别目标.

1 稳健估计理论

稳健估计[6]从概率统计学上可理解为一种切尾均值估计，切尾均值是对均值的改进，这是因为异常值或离群值会使得均值估计失真，离群值会使得均值偏向自己的一方以寻找平衡点，因而歪曲了均值作为平均水平度量的意义.稳健估计正是通过切尾的方式来规避掉那些极端异常点的影响，可以理解为是去掉极大、极小数据，对其余的数据作平均.例如，切尾率为5%的切尾均值就是指去掉5%的最大值和最小值之后，对剩余90%的数据平均所得到的结果.由此可见，普通均值受到离群值的影响较大，而相比之下中值则比较稳健.

对于跟踪的目标信号可理解为按照某种分布来排列的统计概率密度函数，而背景和强噪声数据可以理解为离群值，因此需要一个介于中值估计和均值估计之间的滤波结构，即稳健估计结构.

稳健估计可以看作数据向量的中值和均值的一个凸组合，可描述为

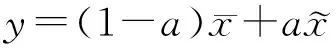
(1)

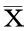
(2)

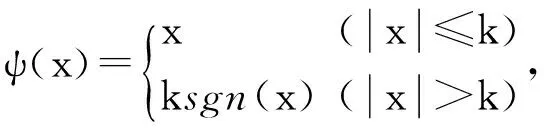
(3)

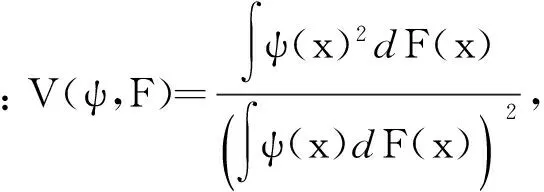
通过稳健估计可以得到一种基于目标跟踪的切尾均值概率估计算法，对Meanshift算法中的均值估计过程进行修正，可提高算法对噪声的抵抗能力和跟踪的准确性.

2 修正Meanshift算法

经典的Meanshift算法是通过定义一族核密度函数来分别计算目标和跟踪区域内像素的关联度，利用概率密度梯度下降原理，实现跟踪值向计算的核密度均值移动，再通过设置相似度函数，计算关联性.当相似关联度之间的差别小于给定的阈值时，计算收敛，得到跟踪目标的位置.Meanshift变量的一般数学描述为

(4)

式中：Ω为样本点集合；xi-x为样本点xi相对于选定参考点x的位置偏移量.由于样本采样越靠近参考点x，其相对于估计均值越可靠，常用扩展形式为

(5)

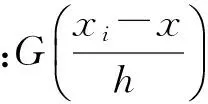
(6)

式中：Ch为归一化常数因子；g为核密度函数的距离函数；δ(f(xi))为delta函数，判定样本点是否属于目标点.

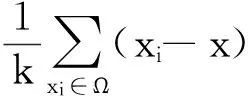
(7)

按照Meanshift算法的一般流程，计算候选目标和目标模型之间的相似度，通常采用Bhattacharrya系数ρ表征候选目标和目标模型之间的匹配度，匹配度越大，则越可能是目标区域.一般采用阈值比较的方式来确定目标位置，当ρ的取值超过一个阈值，或相邻两次计算得到的ρ之间的差值小于一个阈值时，停止迭代，并输出当前目标的位置.

3 实验设计和结果

为了验证本文提出的目标追踪系统的有效性，文中利用仿真数据和实际拍摄的视频进行了相应的结果验证.具体的仿真参数ρ=0.95，k=1.5，a=0.5，归一化参数Ch依据每次实际计算迭代更新.仿真数据模拟了一个大小可变的发光体在噪声背景下进行螺旋线运动，仿真数据信噪比分别为60、30和0db，分别记录传统Meanshift算法与本文提出的修正Meanshift算法对于目标跟踪的轨迹数据，并分析算法得到的数据和实际模拟轨道数据之间的误差.

图1展示了用于仿真的螺旋线轨迹，实际选取了500个目标移动位置，每个位置用*型符号表示，仿真的发光体按照图1描绘的轨迹位置移动，其移动距离为无量纲单位，移动范围在x-y平面坐标所形成的矩形内.

通过仿真目标的追踪，测试了在信噪比为60和30db时修正Meanshift算法的跟踪效果，如图2、3所示.当信噪比为0db时，将传统Meanshift算法与修正Meanshift算法进行跟踪效果比较，如图4、5所示.修正Meanshift算法和经典Meanshift算法虽均能够跟踪目标，但传统算法的跟踪抖动更加明显，且误差更大.进一步减少信噪比后，两者的差异则会更加凸显.当信噪比为0 db时，传统算法在45帧后出现了跟踪目标丢失情况，无法继续跟踪发光小球，而相应的修正算法却始终表现稳健.

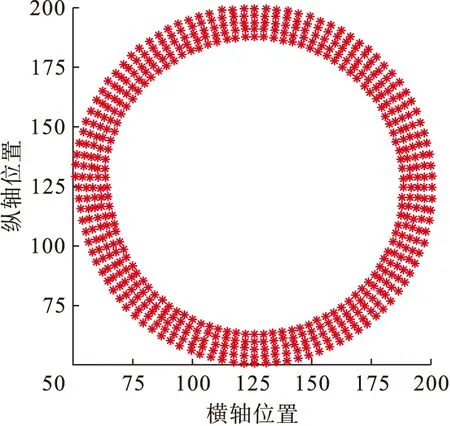
图1 仿真发光体的运动轨迹Fig.1 Moving trajectory of simulated illuminator

图2 修正算法追踪发光体(SNR=60 db)Fig.2 Modified algorithm for tracking illuminator(SNR=60 db)

图6给出了仿真发光体的理论轨迹和实际通过修正方法估计的轨迹对比，可从图6上直观地看出，基于修正方法的估计轮廓和真实数据基本一致，其准确地跟踪出了发光体的运动轨迹.

图7给出了实际测量计算得到的目标追踪在横轴和纵轴上的绝对误差；图8给出了修正算法横轴的相对误差，从图8中可看出，整体目标追踪的相对误差被控制在1.5%以内，证明修正算法在强噪声环境下鲁棒的优越性.

图3 修正算法追踪发光体(SNR=30 db)Fig.3 Modified algorithm for tracking illuminator(SNR=30 db)

图4 经典Meanshift算法追踪发光体(SNR=0 db)Fig.4 Traditional Meanshift algorithm for tracking illuminator(SNR=0 db)

为了进一步验证本文方法的实用性，在实际的视频数据中进行了测试，目标为一只敲击乐器的手，其手部在从左向右运动的过程中，还伴随了上下位移，同时因为手持敲击器具，器具可看作是识别手部的干扰噪声.传统的Meanshift方法在跟踪时会发生丢失，从第23帧开始无法跟上手部动作，而本文提出的结合稳健估计和Meanshift算法的修正方法表现得更加稳定，能够准确跟踪运动目标，修正算法的跟踪效果如图9所示.

图5 修正算法追踪发光体(SNR=0 db)Fig.5 Modified algorithm for tracking illuminator(SNR=0 db)

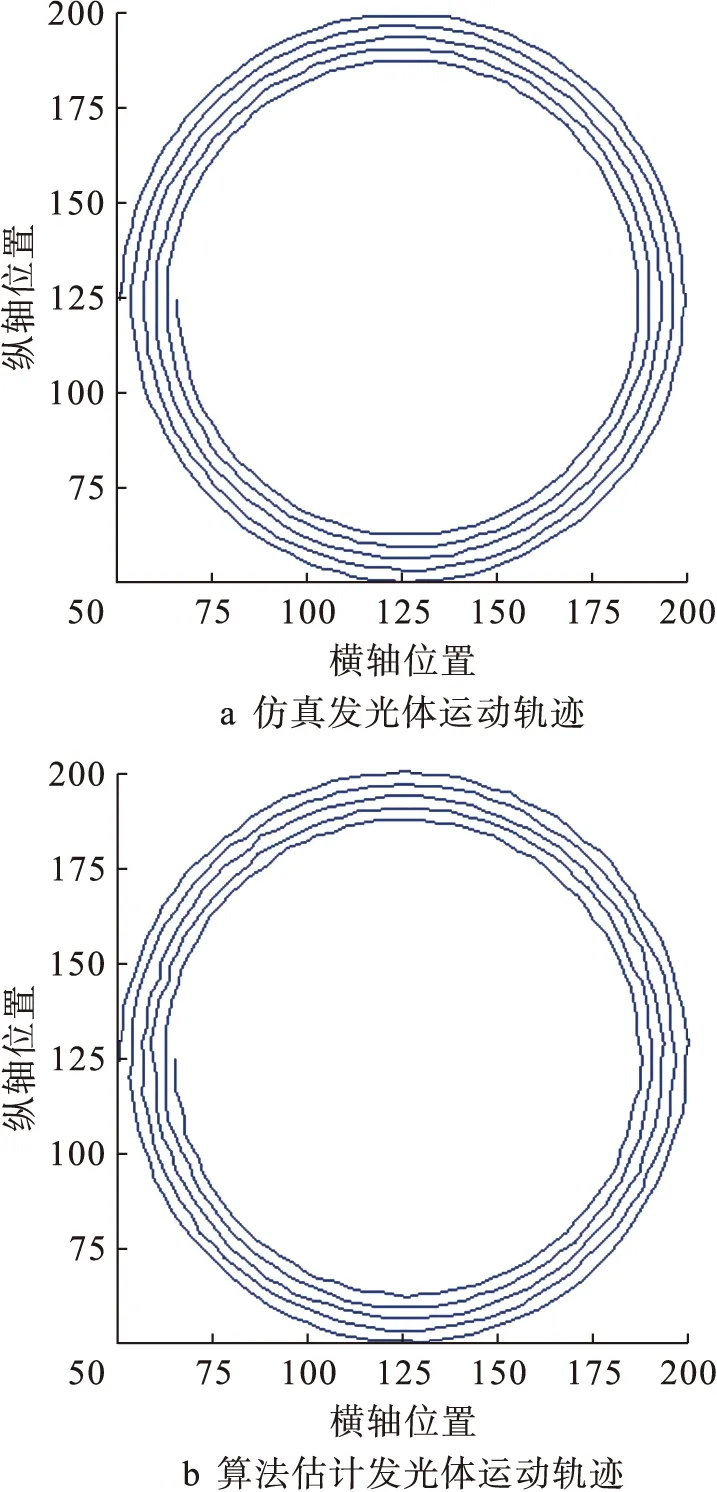
图6 修正算法追踪发光体轨迹比较(SNR=0 db)Fig.6 Comparison in modified algorithm for tracking trajectory of illuminator(SNR=0 db)

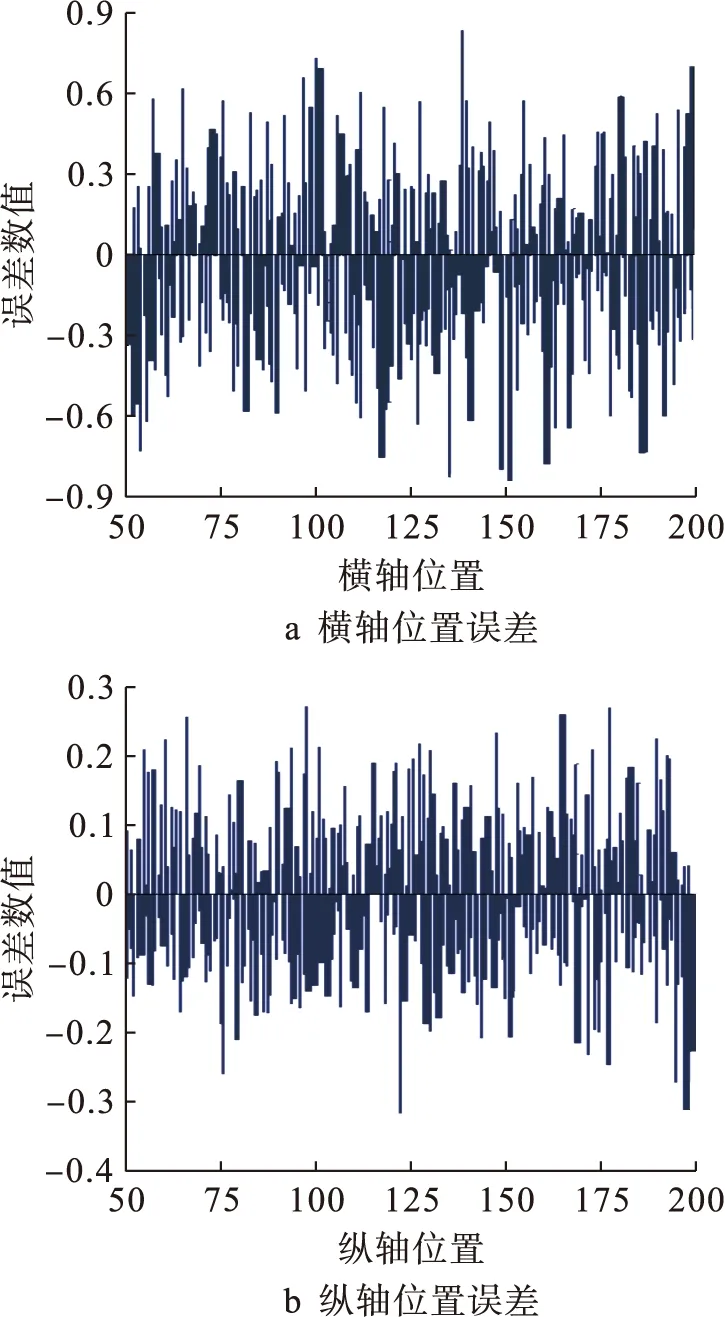
图7 修正算法绝对误差(SNR=0 db)Fig.7 Absolute error of modified algorithm(SNR=0 db)

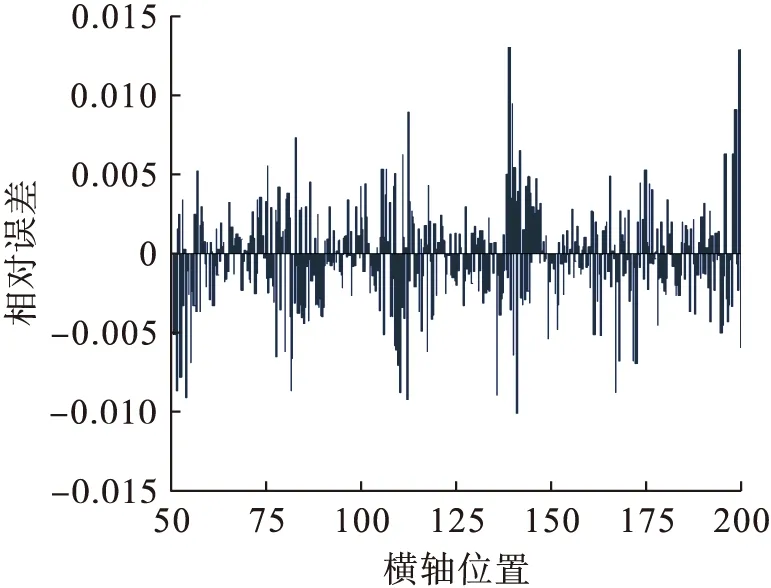
图8 修正算法相对误差(SNR=0 db)Fig.8 Relative error of modified algorithm(SNR=0 db)

4 结 论

本文提出一种结合稳健估计和Meanshift算法的视频目标追踪系统，通过切尾均值替换Meanshift算法中的均值，可以使目标跟踪的稳定度更高，尤其是针对强噪声环境下的目标，本文算法较传统算法表现出了较强的抗干扰能力.下一步的研究主要考虑融合其他滤波算法(例如粒子滤波)来进一步提升追踪的准确性.

图9 修正算法追踪敲击的手(SNR=0 db)Fig.9 Modified algorithm for tracking knocking hand(SNR=0 db)

[1]陈双叶，王善喜.基于五帧差分和改进Meanshift算法的运动目标跟踪 [J].计算机科学，2016，43(增刊1)：203-206.

(CHEN Shuang-ye，WANG Shan-xi.Moving object tracking based on five-frame difference and modified Meanshift algorithm [J].Computer Science，2016，43(Sup1)：203-206.)

[2]聂振钢，孙协昌，梁银川.基于多特征Mean-Shift的灵巧弹药末制导跟踪算法 [J].微电子学与计算机，2016，33(5)：89-91.

(NIE Zhen-gang，SUN Xie-chang，LIANG Yin-chuan.Mechanical trajectory tracking algorithm based on multi-feature Mean-Shift for smart ammunition [J].Microelectronics and Computer，2016，33(5)：89-91.)

[3]李扬.基于视频序列的运动目标追踪算法 [J].电子科技，2012，25(8)：125-127.

(LI Yang.A moving target tracking algorithm based on video sequence [J].Electronic Science and Technology，2012，25(8)：125-127.)

[4]毛晓波，郝向东，梁静.基于ELM与Mean Shift的抗遮挡目标跟踪算法 [J].郑州大学学报(工学版)，2016，37(1)：1-5.

(MAO Xiao-bo，HAO Xiang-dong，LIANG Jing.Anti-occlusion target tracking algorithm based on ELM and Mean Shift [J].Journal of Zhengzhou University(Engineering Science)，2016，37(1)：1-5.)

[5]王强.基于视觉传感网络的目标跟踪系统设计 [J].现代电子技术，2016，39(8)：88-91.

(WANG Qiang.Design of target tracking system based on vision sensor network [J].Modern Electronics Technology，2016，39(8)：88-91.)

[6]Guo Y F.Robust statistic and comparative analysis of the robustness of the statistic [J].Statistical Research，2007(9)：82-84.

[7]Cheng Y.Meanshift mode seeking clustering [J].IEEE Transactions on Pattern Analysis &Machine Intelligence，1995，17(8)：790-799.

[8]Salhi A.Object tracking system using Camshift，Meanshift and Kalmanfilter [J].World Academy of Science Engineering &Technology，2012，64(6)：574-578.

[9]Lei B.Design and realization of the tracking system based on Meanshift algorithm [J].Electronic Mea-surement Technology，2016(8)：98-105.

[10]Morandeira N S，Grimson R，Kandus P.Assessment of SAR speckle filters in the context of object-based image analysis [J].Remote Sensing Letters，2016，7(2)：150-159.

[11]Razavi S F，Sajedi H，Shiri M E.Integration of color and uniform interlaced derivative patterns for object tracking [J].Image Processing，2016，10(5)：381-390.

[12]尤天来，卓炳荣.基于自适应尺度的Mean-shift跟踪算法 [J].现代电子技术，2011，34(10)：95-97.

(YOU Tian-lai，ZHUO Bing-rong.A Mean-shift tracking algorithm based on adaptive scale [J].Modern Electronics Technique，2011，34(10)：95-97.)

[13]王保云，范保杰.基于颜色纹理联合特征直方图的自适应Meanshift跟踪算法 [J].南京邮电大学学报(自然科学版)，2013，33(3)：18-25.

(WANG Bao-yun，FAN Bao-jie.Adaptive Meanshift tracking algorithm based on color texture combined with feature histogram [J].Journal of Nanjing University of Posts and Telecommunications(Natural Science Edition)，2013，33(3)：18-25.)

(责任编辑：景 勇 英文审校：尹淑英)

Video target tracking algorithm with combining robust estimation and Meanshift

ZHU Wen-ya1,2

(1.School of Economics and Management,Wuhan University,Wuhan 430072,China;2.School of Mechanical and Electrical Information,Yiwu Industrial &Commercial College,Yiwu 322099,China)

Aiming at the problem that the Meanshift algorithm is sensitive to the strong noise environment,a modified Meanshift algorithm with combining the robust estimation and traditional Meanshift was proposed.The kernel probability density function of traditional Meanshift algorithm was modified through the robust estimation,and the robustness of Meanshift algorithm got improved.Aiming at the simulation data with signal to noise rate (SNR) of 60,30 and 0 db,the accuracy and precision of the tracking trajectory of both traditional and modified Meanshift algorithms were compared.The results indicate that the modified Meanshift algorithm can achieve the accurate tracking of targets,and the relative error of tracking position is below 1%.For the real video data of moving targets,the proposed algorithm can also realize the real time tracking and positioning,and can overcome the target tracking missing problem of traditional Meanshift algorithm.

robust estimation;Meanshift;target tracking;noise;kernel probability density function;median;error;video

2016-11-01.

浙江省高等教育教学改革项目(JG2015343).

朱闻亚(1980-)，男，安徽阜阳人，副教授，博士生，主要从事计算机软件理论、网络安全等方面的研究.

02 17∶28在中国知网优先数字出版.

http：∥www.cnki.net/kcms/detail/21.1189.T.20170302.1728.018.html

10.7688/j.issn.1000-1646.2017.02.11

TP 391

A

1000-1646(2017)02-0177-06