雷达目标跟踪中的典型非线性滤波算法研究

郑作虎　欧阳东升　李黎明

(95806部队　北京　100076)

0　引言

在雷达信号处理领域，如何实现对目标运动状态的准确估计是研究的重点内容，由于目标运动模型的非线性非高斯特性，非线性滤波算法在雷达目标跟踪中有着广泛的应用，目前，主要包括扩展卡尔曼滤波[1](Extend Kalman Filter，EKF)、不敏卡尔曼滤波[2](Unscented Kalman Filter, UKF)和粒子滤波算法[3](Particle Filter, PF)。其中，EKF是一种次优滤波算法，通过一阶泰勒级数展开近似非线性系统，进而得到线性系统的最优解，但一阶泰勒级数近似的线性化误差较大，导致算法滤波精度较差；UKF利用不敏变换较好解决了非线性问题，通过一系列采样点逼近概率密度函数，不需要进行线性化处理，但在非高斯噪声环境下性能下降；PF是一种基于蒙特卡罗方法和递推贝叶斯估计的统计滤波方法，其基本思想是通过序贯重要性采样(Sequential Importance Sample, SIS)算法采样一组随机加权粒子来近似后验概率密度函数(Probability Density Function, PDF)，以均值运算代替积分运算，最终获得状态的最小均方估计，当粒子数足够时，可以认为这些粒子的统计特性近似于状态的后验概率分布的统计特性[4]。

与EKF和UKF算法相比，PF算法适用于任何非高斯非线性系统环境，但存在粒子退化问题[5]。解决粒子退化问题的一种方法就是构造好的重要性密度函数[6]，选择标准是逼近于真实的后验PDF，且便于采样；解决粒子退化问题的另一种方法就是重采样[7]，重采样方法在一定程度解决了粒子退化问题，但大量复制权值大的粒子也降低了粒子的多样性，导致了粒子枯竭问题。

1　算法基本原理和实现步骤

1.1　EKF算法

设非线性非高斯状态空间模型为

状态方程：

xk=f(xk-1)+wk

(1)

量测方程：

zk=h(xk)+vk

(2)

式中：xk为k时刻N维状态矢量；yk为k时刻M维量测矢量；wk、vk分别为k时刻系统噪声和量测噪声，相互独立，协方差矩阵分别为Qk和Rk；f(·)，h(·)为有界非线性映射。

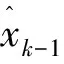
(3)

(4)

(5)

(6)

由式(4)、(6)可知，非线性系统通过泰勒级数展开近似为线性系统，根据KF算法原理，可得EKF算法的基本公式为：

状态预测：

(7)

协方差预测：

(8)

量测预测：

(9)

相应的协方差

(10)

增益：

(11)

状态估计：

(12)

协方差估计：

Pk|k=(I-KkHk)Pk|k-1

(13)

EKF算法的实现步骤为：

(1)系统初始化

(14)

(3)利用式(8)计算状态预测协方差Pk|k-1；

(4) 利用式(11)计算滤波增益Kk；

扩展卡尔曼滤波算法由于其针对非线性模型的简单直观性，近年来已经得到了广泛的应用，但它也有以下不足：(1)由于采用一阶泰勒级数近似线性化，线性化误差较大，导致EKF滤波算法精度变差，甚至发生滤波发散问题；(2)EKF滤波算法需要计算非线性系统的雅可比矩阵，但通常不易实现；(3)EKF算法要求非线性系统必须是连续可微的，限制了其应用范围[8]。

1.2　UKF算法

不敏卡尔曼滤波基于不敏变换(Unscented Transformation，UT)，在UT过程中，重点是采样Sigma采样点，实际中一般采用对称采样，计算简单，滤波精度可达到2阶泰勒级数展开。UT主要实现步骤为：

Step1首先计算2nx+1个Sigma采样点和相对应的权值

(15)

(16)

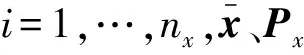
Step2每个Sigma采样点通过非线性函数传播

yj=f(χj)j=0,…,2nx

(17)

Step3ny的估计均值和协方差为

(18)

(19)

基于UT，UKF算法的实现步骤为：(1)利用式(14)进行系统初始化。

(2)利用式(15)、(16)计算状态Sigma采样点ξj(k-1|k-1)和其相应的权值Wj，根据式(1)计算Sigma采样点的一步预测值：

ξj(k|k-1)=f(ξj(k-1|k-1))

(20)

(3)利用ξj(k|k-1)及权值Wj，根据式(18)、(19)计算状态预测值和相应的协方差预测值

(21)

(22)

(4)根据式(2)，计算量测采样点的一步预测值

ζj(k|k-1)=h(ξj(k|k-1))

(23)

(5)根据式(18)、(19)计算量测预测值和相应的协方差预测值

(24)

(25)

(6)计算滤波增益值

(26)

相对EKF算法，UKF算法滤波精度有了很大的提高，应用范围也宽广了很多，但算法仅具有二阶滤波精度，且仅适用于高斯系统。

1.3　PF算法

根据蒙特卡罗方法，对于k时刻目标状态的后验PDF，可用一系列加权粒子表示为

(27)

(28)

(29)

假定系统当前状态和未来量测无关，且系统状态服从马尔科夫过程，则π(x0:k|z1:k)可分解为

π(x0:k|z1:k)=π(xk|xk-1,zk)π(x0:k-1|z1:k-1)

(30)

同理，状态后验PDF可表示为

∝p(zk|xk)p(xk|xk-1)p(x0:k-1|z1:k-1)

(31)

将式(30)、式(31)代入式(29)，则重要性权值可表示为

(32)

在PF中，重要性密度函数与真实的后验PDF的逼近程度直接影响着算法滤波性能，逼近程度越高，粒子权值方差越小，滤波性能越好。研究表明，使粒子权值方差最小的最优重要性密度函数为

(33)

将式(33)代入式(32)可得

(34)

(35)

将式(35)代入式(32)可得

(36)

将权值归一化

(37)

则系统状态的最小均方估计为

(38)

直接根据状态先验PDF采样粒子，容易实现，权值计算也仅与前一时刻的粒子权值和似然函数有关，计算简单。但是，在量测精度较高的场合(量测噪声较小)，状态先验PDF与状态后验PDF存在较大偏差，这样根据状态先验PDF采样的粒子与真实状态偏差较大，随着迭代过程的进行，权值小的粒子越来越多，权值大的粒子越来越少，导致权值方差越来越大，加剧了粒子退化问题。

为了解决粒子退化问题，标准PF通常在SIS之后进行重采样。通过复制大权值粒子，去掉小权值粒子，重采样算法从估计的后验PDF上重新抽取N个独立同分布的粒子集，其相应权值为1/N，能够降低粒子权值方差，提高有效粒子数，改善滤波精度，但重采样算法也导致了样本枯竭问题，损失了粒子的多样性。

标准PF算法的实现步骤为：

(1)初始化；

(2)计算k时刻粒子权值；

(3)重采样；

(4)k时刻系统状态估计。

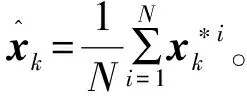
2　实验与分析

采用文献[9]中典型的一维非线性非高斯模型，对EKF、UKF、PF三种算法的滤波性能进行比较分析。状态方程和量测方程分别为：

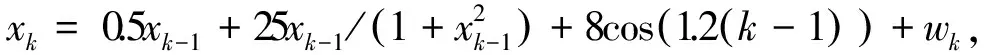
k=0,1,…,k-1

(39)

(40)

参数设置如下：状态噪声wk～Gamma(3,2)，量测噪声vk～N(0,1)，初始状态x0=1，初始状态方差p(x0)=1，时间序列长度K=60，UKF的参数取κ=2，PF粒子数N=100。本文对各滤波方法进行M=100次的Monte Carlo仿真，各滤波算法每一时刻的均方根误差为

(41)

为了比较EKF、UKF、PF算法滤波性能，图1给出了三种算法滤波状态估计值与真实值的比较曲线。从图中可以看出，PF算法的滤波状态最接近于真实状态，滤波性能优于EKF、UKF算法；因较好地解决了非线性问题，UKF算法滤波性能优于EKF；EKF存在线性化误差，滤波性能最差。

为了更精确比较三种算法的滤波性能，图2给出了Monte Carlo仿真100次时三种算法均方根误差曲线的比较，表1给出了均方根误差的均值和方差比较。从中可以看出，PF算法的均方根误差最小，表明最接近于真实的状态值，且最平稳，滤波性能最优，UKF算法次之，EKF算法最差。

3　结束语

本文详细介绍了基本PF算法的基本原理和实现步骤，并在典型的一维非线性非高斯模型下综合比较了PF与EKF、UKF三种算法的滤波性能。实验结果表明，在非线性非高斯条件下，PF算法的滤波性能优于其他两种算法，且随着粒子数的增多，算法滤波性能更优。

表1EKF、UKF、PF算法均方根误差比较

算法均方根误差均值方差EKF36．32102291UKF16．615929．8329PF1．12300．3190

参考文献:

[1]夏楠,邱天爽,李景春,等.一种卡尔曼滤波与粒子滤波相结合的非线性滤波算法[J].电子学报,2013,41(1):148-152.

[2]申正义,王晴晴,王洪林,等. 基于修正SUKF的固定单站无源定位跟踪算法[J].火控雷达技术,2015,44(1):38-42.

[3]王首勇,万洋,刘俊凯,等.现代雷达目标检测理论与方法(第二版)[M].北京:科学出版社,2015.

[4]万洋,王首勇.非线性滤波算法的性能分析[J]. 空军雷达学院学报,2010,24(2):111-114.

[5]郑作虎,王首勇.一种基于GHF的高斯粒子滤波算法[J].控制与决策,2014,29(9):1698-1702.

[6]张俊根.粒子滤波及其在目标跟踪中的应用研究[D].西安:西安电子科技大学,2011.

[7]赵玲玲.目标跟踪中的粒子滤波与概率假设密度滤波研究[D].哈尔滨:哈尔滨工业大学,2011.

[8]陈亮.机动目标跟踪关键技术研究[D].哈尔滨:哈尔滨工程大学,2012.

[9]gordon n, salmond d, smith a.Novel Approach to Nonlinear/Non-Gaussian Bayesian State Estimation[J].IEE Proceeding on Radar,Sonar and Navigation,1993,140(2):107-113.