非弹性碰撞之困惑

李俊峰

(清华大学航天航空学院，北京100084)

教授讲题

非弹性碰撞之困惑

李俊峰1)

(清华大学航天航空学院，北京100084)

题目

一根长为2a的均匀杆与竖直线成θ角，自高处无初速落下,与光滑水平地面作完全非弹性碰撞，杆下端与地面接触后又立刻离开地面，问：杆下落高度H应满足什么条件？假设杆始终在竖直平面内运动. (改编自：李俊峰、张雄编著《理论力学(第2版)》习题7.31)

解题思路

这个问题的难点在于，按照学生以前学习中形成的习惯看法，“完全非弹性碰撞”和“杆下端与地面接触后又立刻离开地面”这两个说法是相互矛盾的，让学生困惑，我们先给出相应的数学表达.设杆下端为A，杆质心为C，建立直角坐标系(如图1所示)，Ax轴沿着地面.“完全非弹性碰撞”的数学表达：碰撞后瞬时A点速度的竖直分量uAy=0.“杆下端与地面接触后又立刻离开地面”的数学表达：碰撞后瞬时地面的压力N=0并且A点加速度的竖直分量aAy＞0

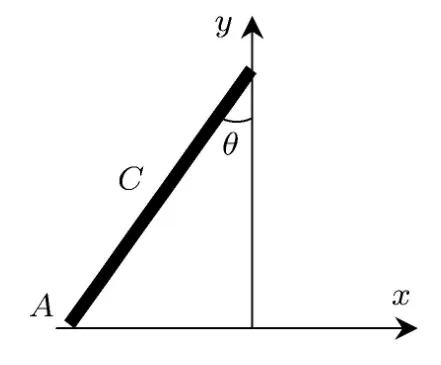
图1

下面分两个子问题来研究.

首先，研究刚体碰撞问题，我们可以利用动量定理和动量矩定理的积分形式，由碰撞前瞬时杆的角速度和质心速度，求得碰撞后瞬时杆的角速度和质心速度.

在杆下落过程中作刚体平动，在碰撞前瞬√时，杆的角速度为零，杆上所有点的速度都等于2gH.

设碰撞后瞬时杆的角速度为ω，质心速度的水平和竖直分量分别为uCx和uCy，由于地面光滑，不能给杆水平冲量，故碰撞后瞬时质心速度的水平分量仍然是零，与碰撞前一样.设碰撞过程中地面给杆的竖直冲量为Iy(重力等常规力的冲量可以忽略)，根据动量定理和动量矩定理的积分形式，有

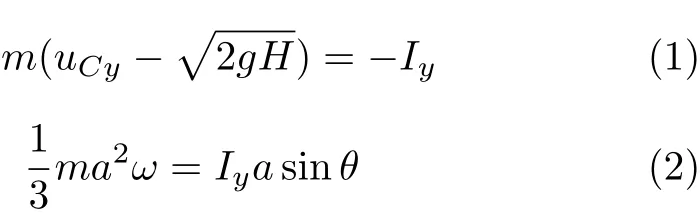
这两个动力学方程包括3个未知数：ω，uCy，Iy，需要再补充一个运动学关系式.我们注意到，碰撞后瞬时杆作平面运动，C点速度沿着竖直方向，A点速度沿着水平方向(完全非弹性碰撞uAy=0).可知，瞬时速度中心为C∗(如图2所示)，由此可得

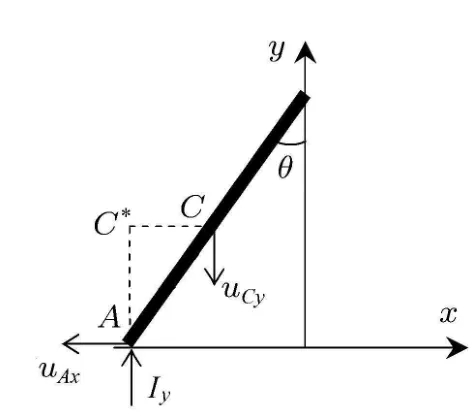
图2

动力学方程(1)～(2)及运动学补充条件(3)联立解得

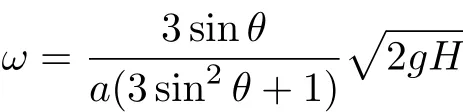
接下来，利用质心运动定理和动量矩定理，分析碰撞结束后瞬时杆的瞬时角加速度和质心加速度.碰撞后瞬时，不再有碰撞冲量作用，杆在重力作用下运动(地面压力N=0).容易判断，此瞬时杆的角加速度为零，杆质心加速度即为重力加速度.以C为基点计算A点的加速度可得aAy=ω2acosθ-g，再利用前面求出的ω和“杆下端与地面接触后又立刻离开地面”条件之一aAy＞0，可得

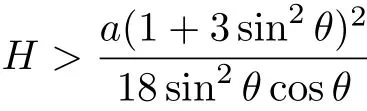
10.6052/1000-0879-16-399

(责任编辑：胡 漫)

本文于2016-12-08收到.

1)E-mail：lijunf@mail.tsinghua.edu.cn

李俊峰.非弹性碰撞之困惑.力学与实践,2017,39(1)：86-87

Li Junfeng.Confussion about non-elastic collision.Mechanics in Engineering,207,39(1)：86-87